人教版数学九年级下册27.3两个位似图形坐标之间的关系课件((共18张ppt)
文档属性
| 名称 | 人教版数学九年级下册27.3两个位似图形坐标之间的关系课件((共18张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 151.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-03 00:00:00 | ||
图片预览




文档简介
27.3.2坐标与位似
学习目标
1.理解掌握位似图形在平面直角坐标系上的应用,即会根据相似比,求位似图形顶点,以及根据位似图形对应点坐标,求位似图形的相似比和在平面直角坐标系上作出位似图形.
2.在应用有关知识解决问题的过程中,提高应用意识,体验数形结合的思想方法在解题中的运用.
(一)复习回顾
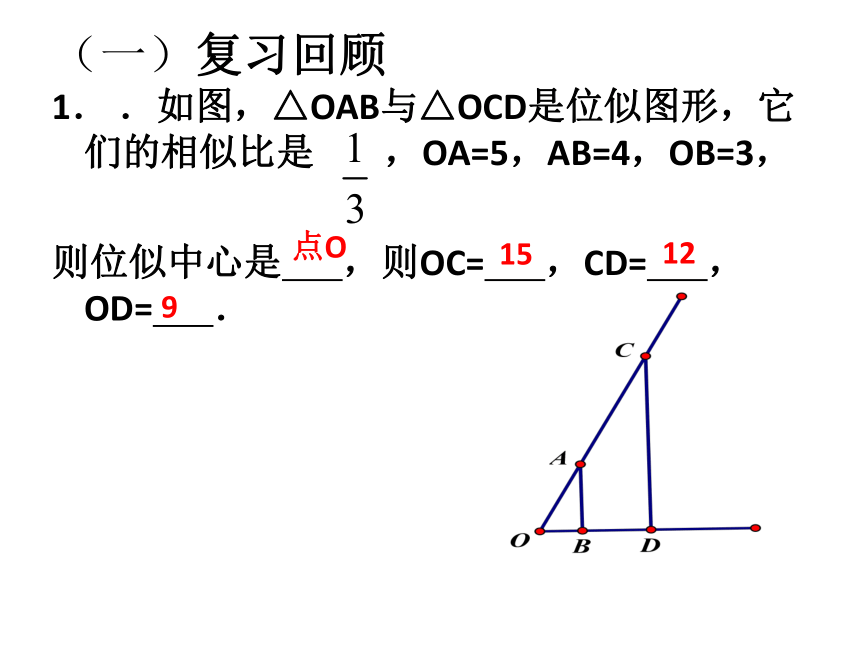
1. .如图,△OAB与△OCD是位似图形,它们的相似比是 ,OA=5,AB=4,OB=3,
则位似中心是 ,则OC= ,CD= ,OD= .
点O
15
12
9
2.在平面直角坐标系中,若点A的坐标为(2,3),则点A关于x轴对称的点的坐标是 ,关于y轴对称的点的坐标是 ,关于原点对称的点的坐标是 .
(2,-3)
(-2,3)
(-2,-3)
(二)问题探究
1.如图在平面直角坐标系中,有两点A(6,3),B(6,0).以原点O为位似中心,相似比为 ,把线段AB缩小.请写出点A’与点A’’的坐标,观察对应点之间坐标的变化,你有什么发现?
线段AB的端点坐标
A(6,3)
B(6,0)
对应点坐标
A'( , )
B'( , )
A''( , )
B''( , )
2
1
-2
-1
2
0
-2
0
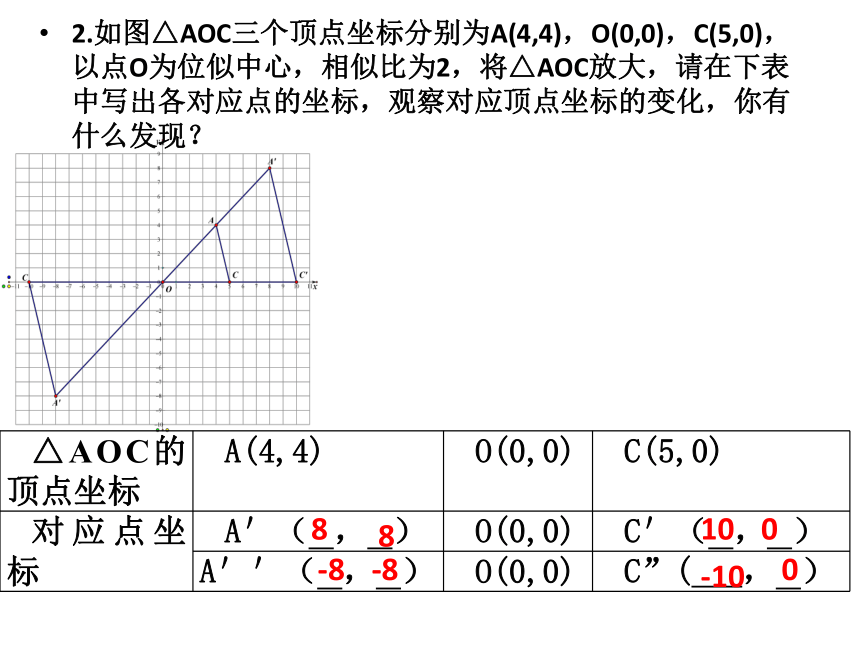
2.如图△AOC三个顶点坐标分别为A(4,4),O(0,0),C(5,0),以点O为位似中心,相似比为2,将△AOC放大,请在下表中写出各对应点的坐标,观察对应顶点坐标的变化,你有什么发现?
△AOC的顶点坐标
A(4,4)
O(0,0)
C(5,0)
对应点坐标
A'( , )
O(0,0)
C'( , )
A''( , )
O(0,0)
C”( , )
8
8
-8
-8
10
0
-10
0
线段AB的端点坐标
A(6,3)
B(6,0)
对应点坐标
A'( , )
B'( , )
A''( , )
B''( , )
△AOC的顶点坐标
A(4,4)
O(0,0)
C(5,0)
对应点坐标
A'( , )
O(0,0)
C'( , )
A''( , )
O(0,0)
C”( , )
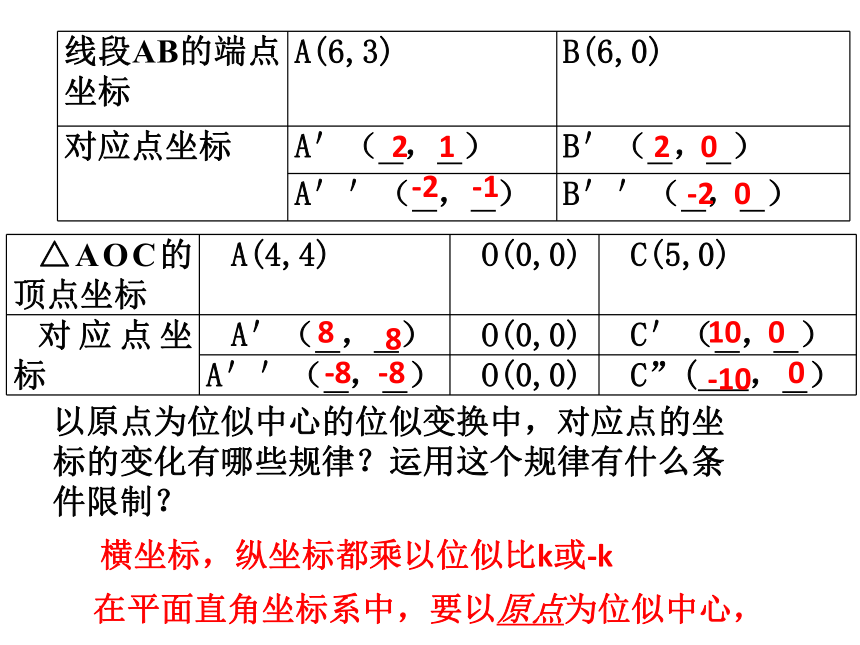
以原点为位似中心的位似变换中,对应点的坐标的变化有哪些规律?运用这个规律有什么条件限制?
横坐标,纵坐标都乘以位似比k或-k
在平面直角坐标系中,要以原点为位似中心,
2
1
-2
-1
2
0
-2
0
8
8
-8
-8
10
0
-10
0
小结:在平面直角坐标系中,如果以原点为位似中心,画出一个与原图形位的图形,使它与原图形的相似比为k,那么与原图形上的点(x,y)对应的位似图形上的点坐标分为两种情况:当两个图形在原点的同侧时,对应点坐标为 ;当两个图形在原点的两侧时,对应点坐标为 .
(kx,ky)
(-kx,-ky)
(三)例题讲解
例1 如图,△ABC的三个顶点坐标分别为A(-2,4),B(-3,1),C(-1,1) ,以原点O为位似中心相似比为2,在第二象限内将△ABC放大,放大后得到△A’B’C’ .出A’,B’,C’的坐标;(点A,B,C的对应点分别是A’,B’,C’),画出放大后的△A’B’C’.
解: A(-4,8),B(-6,2),C(-2,2)
∴ △A’B’C’为所求
小结:画位似图形,通常先求出关键点的对应点的坐标,再描点,连线得到位似图形。
2.在平面直角坐标系中,已知点E(-4,2),F(-2,-2),以原点O为位似中心,相似比为 ,把△OEF缩小.则点E的对
应点E’的坐标是 ,点F的对应点F’的坐标是 .
变式练习
1.如图,△OAB的三个顶点的坐标分别为A(3,0),B(3,2) ,O(0,0),若△OAB与△COE为位似图形,位似比为 ,则点D的的坐标是 ,点E的的坐
标是 .
有图看图,没图考虑分类讨论
(-2,0)
(-2,-1)或(2,1)
或
x
y
o
4.在平面直角坐标系中, 正方形ABCD的四个顶点的坐标分别为A(-6,6),B(-8,2),C(-4,0),D(-2,4),画出它的一个以原点O为位似中心,相似比为1/2的位似图形.求正方形 的面积.
解:A′( -3,3 ), B′( -4,1 ), C′( -2,0 ), D′( -1,2 ).
B
A
C
D
A′
B′
C′
D′
你还有其他办法吗?试试看.
所以正方形ABCD为所求.
如图,以某点为位似中心,将△AOB进行位似变换得到△CDE,记△AOB与△CDE对应边的比为k,则位似中心的坐标和k的值分别为( )
A.(0,0),2 B.(2,2),
C.(2,2),2 D.(2,2),3
例2
3
6
小结:
位似中心是对应点连线的交点,位似比是对应边的比
C
5.如图, △ABC与△A’B’C’ 是位似图形,且顶点都在格点上,则位似中心的坐标是_______, △ABC与 △A’B’C’的相似比
是_______.
x
O
A
B
C
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
(9,0)
C’
A’
B’
变式训练
6.如图,原点O是△ABC和△A′B′C′的位似中心,点A(1,0)与点A′(-2,0)是对应点,△ABC的面积是 ,则△A′B′C′的面积是________________.
6
(四)师生共同小结
坐标系中点(x,y)的变换
关于x轴对称
关于y轴对称
关于原点对称
关于原点位似对称,位似比为k
坐标
(x,-y)
(-x,y)
(-x,-y)
(kx,ky)或
(-kx,-ky)
综合提高
7.如图,O为原点,B,C两点坐标分别为(3,-1)(2,1)
(1)以O为位似中心在y轴左侧将△OBC放大两倍,并画出图形;
(2)分别写出B,C两点的对应点B`,C`的坐标;
(3)求线段B`C`所在直线的函数解析式
8.如图,△ABC是格点三角形.在建立平面直角坐标系后,点B的坐标为(-1,-1).
(1)把△ABC向左平移8格后得到△A1B1C1,则点B1的坐标为____________
(2)把△ABC绕点C按顺时针方向旋转90o后得到△A2B2C,则点B2的坐标为___________
(3)把△ABC以点A为位似中心放大,使放大前后对应边长的比为1:2,则B3的坐标是_______
x
y
O
A
B
C
(五)布置作业
第11课时作业
学习目标
1.理解掌握位似图形在平面直角坐标系上的应用,即会根据相似比,求位似图形顶点,以及根据位似图形对应点坐标,求位似图形的相似比和在平面直角坐标系上作出位似图形.
2.在应用有关知识解决问题的过程中,提高应用意识,体验数形结合的思想方法在解题中的运用.
(一)复习回顾
1. .如图,△OAB与△OCD是位似图形,它们的相似比是 ,OA=5,AB=4,OB=3,
则位似中心是 ,则OC= ,CD= ,OD= .
点O
15
12
9
2.在平面直角坐标系中,若点A的坐标为(2,3),则点A关于x轴对称的点的坐标是 ,关于y轴对称的点的坐标是 ,关于原点对称的点的坐标是 .
(2,-3)
(-2,3)
(-2,-3)
(二)问题探究
1.如图在平面直角坐标系中,有两点A(6,3),B(6,0).以原点O为位似中心,相似比为 ,把线段AB缩小.请写出点A’与点A’’的坐标,观察对应点之间坐标的变化,你有什么发现?
线段AB的端点坐标
A(6,3)
B(6,0)
对应点坐标
A'( , )
B'( , )
A''( , )
B''( , )
2
1
-2
-1
2
0
-2
0
2.如图△AOC三个顶点坐标分别为A(4,4),O(0,0),C(5,0),以点O为位似中心,相似比为2,将△AOC放大,请在下表中写出各对应点的坐标,观察对应顶点坐标的变化,你有什么发现?
△AOC的顶点坐标
A(4,4)
O(0,0)
C(5,0)
对应点坐标
A'( , )
O(0,0)
C'( , )
A''( , )
O(0,0)
C”( , )
8
8
-8
-8
10
0
-10
0
线段AB的端点坐标
A(6,3)
B(6,0)
对应点坐标
A'( , )
B'( , )
A''( , )
B''( , )
△AOC的顶点坐标
A(4,4)
O(0,0)
C(5,0)
对应点坐标
A'( , )
O(0,0)
C'( , )
A''( , )
O(0,0)
C”( , )
以原点为位似中心的位似变换中,对应点的坐标的变化有哪些规律?运用这个规律有什么条件限制?
横坐标,纵坐标都乘以位似比k或-k
在平面直角坐标系中,要以原点为位似中心,
2
1
-2
-1
2
0
-2
0
8
8
-8
-8
10
0
-10
0
小结:在平面直角坐标系中,如果以原点为位似中心,画出一个与原图形位的图形,使它与原图形的相似比为k,那么与原图形上的点(x,y)对应的位似图形上的点坐标分为两种情况:当两个图形在原点的同侧时,对应点坐标为 ;当两个图形在原点的两侧时,对应点坐标为 .
(kx,ky)
(-kx,-ky)
(三)例题讲解
例1 如图,△ABC的三个顶点坐标分别为A(-2,4),B(-3,1),C(-1,1) ,以原点O为位似中心相似比为2,在第二象限内将△ABC放大,放大后得到△A’B’C’ .出A’,B’,C’的坐标;(点A,B,C的对应点分别是A’,B’,C’),画出放大后的△A’B’C’.
解: A(-4,8),B(-6,2),C(-2,2)
∴ △A’B’C’为所求
小结:画位似图形,通常先求出关键点的对应点的坐标,再描点,连线得到位似图形。
2.在平面直角坐标系中,已知点E(-4,2),F(-2,-2),以原点O为位似中心,相似比为 ,把△OEF缩小.则点E的对
应点E’的坐标是 ,点F的对应点F’的坐标是 .
变式练习
1.如图,△OAB的三个顶点的坐标分别为A(3,0),B(3,2) ,O(0,0),若△OAB与△COE为位似图形,位似比为 ,则点D的的坐标是 ,点E的的坐
标是 .
有图看图,没图考虑分类讨论
(-2,0)
(-2,-1)或(2,1)
或
x
y
o
4.在平面直角坐标系中, 正方形ABCD的四个顶点的坐标分别为A(-6,6),B(-8,2),C(-4,0),D(-2,4),画出它的一个以原点O为位似中心,相似比为1/2的位似图形.求正方形 的面积.
解:A′( -3,3 ), B′( -4,1 ), C′( -2,0 ), D′( -1,2 ).
B
A
C
D
A′
B′
C′
D′
你还有其他办法吗?试试看.
所以正方形ABCD为所求.
如图,以某点为位似中心,将△AOB进行位似变换得到△CDE,记△AOB与△CDE对应边的比为k,则位似中心的坐标和k的值分别为( )
A.(0,0),2 B.(2,2),
C.(2,2),2 D.(2,2),3
例2
3
6
小结:
位似中心是对应点连线的交点,位似比是对应边的比
C
5.如图, △ABC与△A’B’C’ 是位似图形,且顶点都在格点上,则位似中心的坐标是_______, △ABC与 △A’B’C’的相似比
是_______.
x
O
A
B
C
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
(9,0)
C’
A’
B’
变式训练
6.如图,原点O是△ABC和△A′B′C′的位似中心,点A(1,0)与点A′(-2,0)是对应点,△ABC的面积是 ,则△A′B′C′的面积是________________.
6
(四)师生共同小结
坐标系中点(x,y)的变换
关于x轴对称
关于y轴对称
关于原点对称
关于原点位似对称,位似比为k
坐标
(x,-y)
(-x,y)
(-x,-y)
(kx,ky)或
(-kx,-ky)
综合提高
7.如图,O为原点,B,C两点坐标分别为(3,-1)(2,1)
(1)以O为位似中心在y轴左侧将△OBC放大两倍,并画出图形;
(2)分别写出B,C两点的对应点B`,C`的坐标;
(3)求线段B`C`所在直线的函数解析式
8.如图,△ABC是格点三角形.在建立平面直角坐标系后,点B的坐标为(-1,-1).
(1)把△ABC向左平移8格后得到△A1B1C1,则点B1的坐标为____________
(2)把△ABC绕点C按顺时针方向旋转90o后得到△A2B2C,则点B2的坐标为___________
(3)把△ABC以点A为位似中心放大,使放大前后对应边长的比为1:2,则B3的坐标是_______
x
y
O
A
B
C
(五)布置作业
第11课时作业
