人教版数学九年级下册课件 27.2.1 相似三角形的判定(共21张ppt)
文档属性
| 名称 | 人教版数学九年级下册课件 27.2.1 相似三角形的判定(共21张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 823.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-03 09:26:37 | ||
图片预览




文档简介
第二十七章 相 似
27.2.1 相似三角形的判定
第2课时 三边成比例的两个三角形相似
1.复习已经学过的三角形相似的判定定理;
2.掌握利用三边来判定两个三角形相似的方法.(重点、难点)
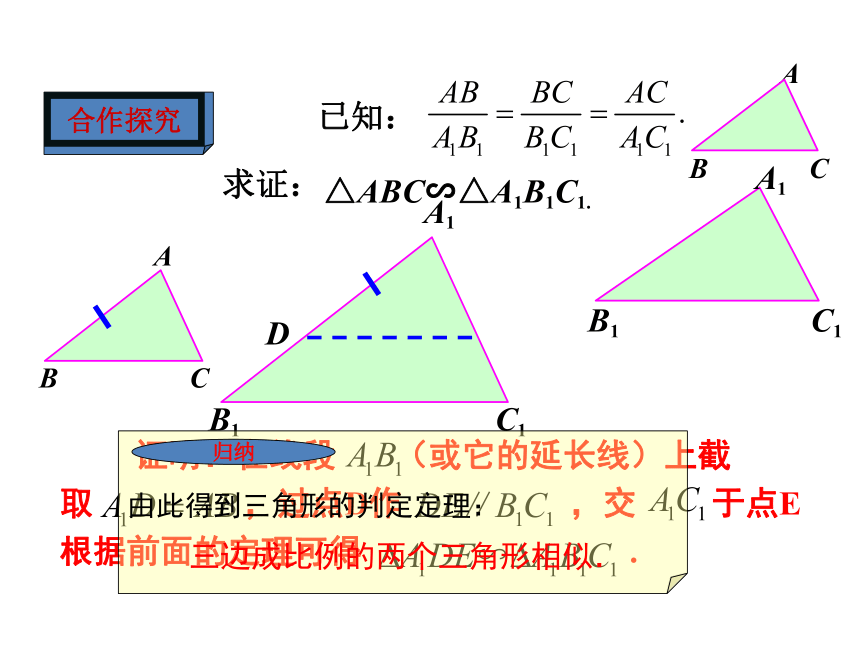
已知:
△ABC∽△A1B1C1.
A1
B1
C1
A
B
C
求证:
A
B
C
D
A1
B1
C1
证明:在线段 (或它的延长线)上截取 ,过点D作 ,交 于点E根据前面的定理可得 .
由此得到三角形的判定定理:
三边成比例的两个三角形相似.
归纳
合作探究
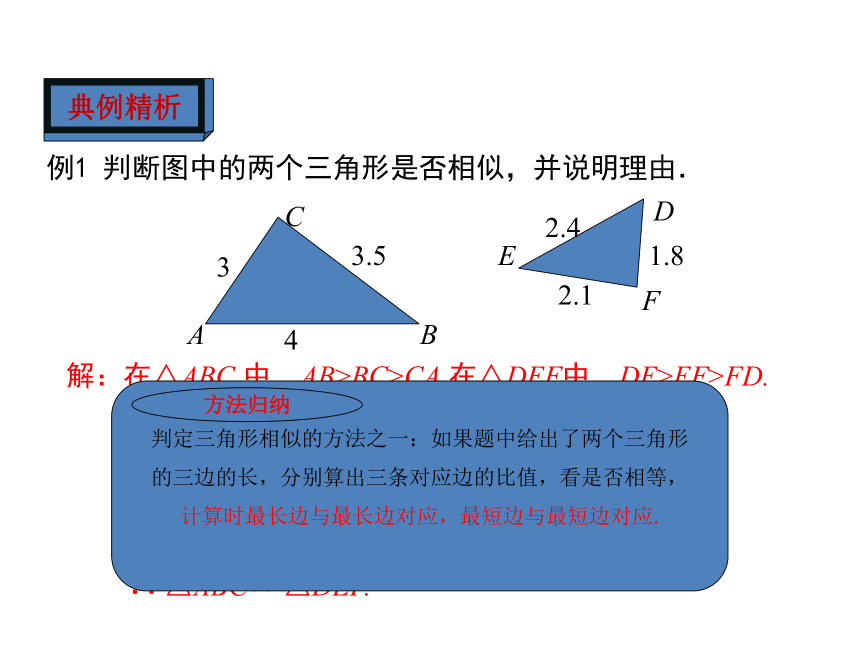
例1 判断图中的两个三角形是否相似,并说明理由.
解:在△ABC 中,AB>BC>CA,在△DEF中,DE>EF>FD.
∴ △ABC∽ △DEF.
A
B
C
D
F
E
3
1.8
3.5
2.1
4
2.4
判定三角形相似的方法之一:如果题中给出了两个三角形
的三边的长,分别算出三条对应边的比值,看是否相等,
计算时最长边与最长边对应,最短边与最短边对应.
方法归纳
典例精析
已知△ABC 和 △DEF,根据下列条件判断它们是否相似.
(3) AB=12, BC=15, AC=24.
DE=16, EF=20, DF=30.
(2)AB=4, BC=8, AC=10.
DE=20, EF=16, DF=8.
(1)AB=3, BC=4, AC=6.
DE=6, EF=8, DF=9.
是
否
否
(注意:大对大,小对小,中对中.)
练一练
例2 如图,在 Rt△ABC 与 Rt△A′B′C′中,
∠C =∠C ′= 90°,且
求证:△ A′B′C′∽△ABC.
证明:由已知条件得AB=2A′B′,AC=2A′C′
从而
BC2 = AB2-AC2 =(2A′B′)2-(2A′C′)2
= 4A′B′2 – 4A′C′2 =4(A′B′2-A′C′2)
= 4B′C′2 =(2B′C′)2.
从而
由此得出,BC=2B′C′,
因此△ A′B′C′∽△ABC.
(三边对应成比例的两个三角形相似)
1.根据下列条件,判断△ABC与△A?B?C?是否相似:
AB=4cm ,BC =6cm ,AC =8cm,A?B?=12cm ,
B?C?=18cm ,A?C?=21cm.
∴△ABC与△A?B?C?不相似.
当堂练习
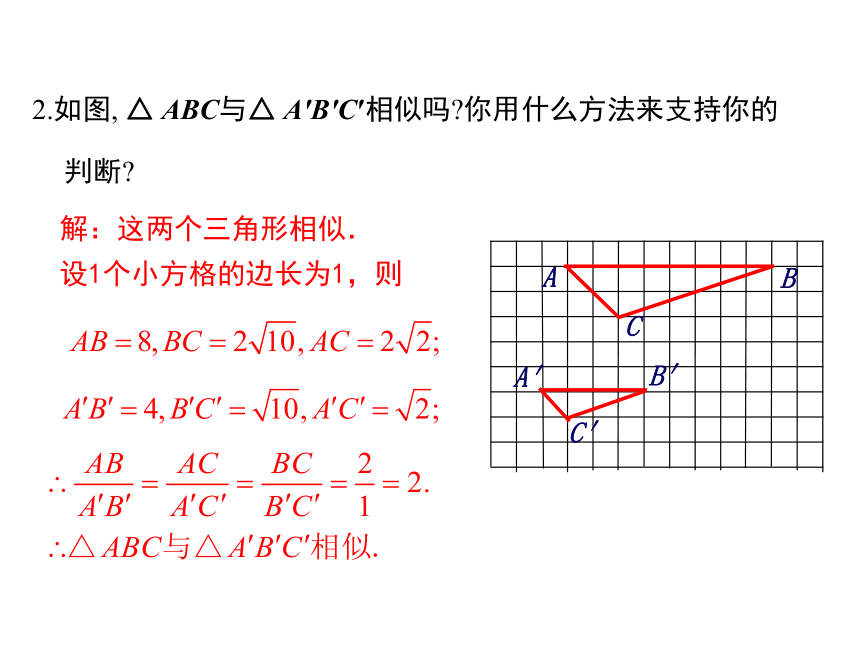
2.如图, △ ABC与△ A′B′C′相似吗?你用什么方法来支持你的判断?
C
B
A
A′
B′
C′
解:这两个三角形相似.
设1个小方格的边长为1,则
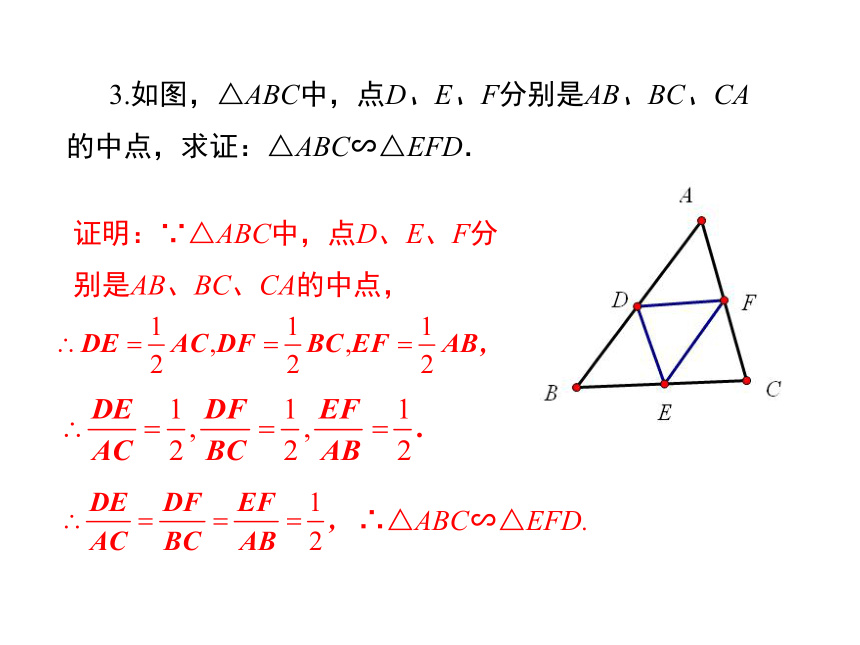
3.如图,△ABC中,点D、E、F分别是AB、BC、CA的中点,求证:△ABC∽△EFD.
∴△ABC∽△EFD.
证明:∵△ABC中,点D、E、F分别是AB、BC、CA的中点,
三边成比例的两个三角形相似
利用三边判定两个三角形相似
相似三角形的判定定理的运用
课堂小结
今日作业
课本第42页习题27.2第1,2(1),3(2)题
第二十七章 相 似
27.2.1 相似三角形的判定
第3课时 两边成比例且夹角相等的两个三角形相似
1.探索“两边成比例且夹角相等的两个角形相似”的判定定理;
2.会根据边和角的关系来判定两个三角形相似.(重点、难点)
问题1 我们学习过哪些判定三角形全等的方法?
问题2 我们目前知道的两个三角形相似有哪些判定方法?
回顾与思考
探 究 2
如图,在△ABC与△A′B′C′中,已知∠A= ∠A′
我们来证明一下前面得出的结论:
△A′B′C′∽△ABC.
B
A
C
D
E
B'
A'
C'
在△A′B′C′的边A′B′上截取点D,使A′D=AB.过点D作DE∥B′C′,交A′C′于点E.
∵DE∥B′C′,
∴△A′DE∽△A′B′C′.
∵A′D=AB,
∴A′E=AC. 又∠A′=∠A.
∴△A′DE≌△ABC,
∴△A′B′C′∽△ABC.
由此得到三角形的判定定理:
两边成比例且夹角相等的两个三角形相似.
归纳
例1 在△ABC和△DEF中,∠C=∠F=70°,AC=3.5cm,
BC=2.5 cm,DF=2.1 cm,EF=1.5 cm.求证:△DEF∽△ABC.
A
F
E
C
B
D
证明:
∵AC=3.5cm,BC=2.5cm,DF=2.1cm,EF=1.5cm,
又∵∠C=∠F=70°,
∴ △DEF∽△ABC(两边成比例且夹角相等的两个三角形相似)
典例精析
?如图,△ABC与△ADE都是等腰三角形,AD=AE,
AB=AC,∠DAB=∠CAE.求证:△ABC∽△ADE.
△ABC∽△ADE.
证明:
练一练
3.2
3.2
2
1.6
50°
)
如果两个三角形的两边成比例,但相等的角不是这两边的夹角,那么两个三角形是否相似呢?画一画,量一量.
探究归纳
两边成比例且夹角相等的两个三角形相似
利用两边及夹角判定三角形相似
相似三角形的判定定理的运用
课堂小结
今日作业
课本第42页习题27.2第2(2),3(2),4题
27.2.1 相似三角形的判定
第2课时 三边成比例的两个三角形相似
1.复习已经学过的三角形相似的判定定理;
2.掌握利用三边来判定两个三角形相似的方法.(重点、难点)
已知:
△ABC∽△A1B1C1.
A1
B1
C1
A
B
C
求证:
A
B
C
D
A1
B1
C1
证明:在线段 (或它的延长线)上截取 ,过点D作 ,交 于点E根据前面的定理可得 .
由此得到三角形的判定定理:
三边成比例的两个三角形相似.
归纳
合作探究
例1 判断图中的两个三角形是否相似,并说明理由.
解:在△ABC 中,AB>BC>CA,在△DEF中,DE>EF>FD.
∴ △ABC∽ △DEF.
A
B
C
D
F
E
3
1.8
3.5
2.1
4
2.4
判定三角形相似的方法之一:如果题中给出了两个三角形
的三边的长,分别算出三条对应边的比值,看是否相等,
计算时最长边与最长边对应,最短边与最短边对应.
方法归纳
典例精析
已知△ABC 和 △DEF,根据下列条件判断它们是否相似.
(3) AB=12, BC=15, AC=24.
DE=16, EF=20, DF=30.
(2)AB=4, BC=8, AC=10.
DE=20, EF=16, DF=8.
(1)AB=3, BC=4, AC=6.
DE=6, EF=8, DF=9.
是
否
否
(注意:大对大,小对小,中对中.)
练一练
例2 如图,在 Rt△ABC 与 Rt△A′B′C′中,
∠C =∠C ′= 90°,且
求证:△ A′B′C′∽△ABC.
证明:由已知条件得AB=2A′B′,AC=2A′C′
从而
BC2 = AB2-AC2 =(2A′B′)2-(2A′C′)2
= 4A′B′2 – 4A′C′2 =4(A′B′2-A′C′2)
= 4B′C′2 =(2B′C′)2.
从而
由此得出,BC=2B′C′,
因此△ A′B′C′∽△ABC.
(三边对应成比例的两个三角形相似)
1.根据下列条件,判断△ABC与△A?B?C?是否相似:
AB=4cm ,BC =6cm ,AC =8cm,A?B?=12cm ,
B?C?=18cm ,A?C?=21cm.
∴△ABC与△A?B?C?不相似.
当堂练习
2.如图, △ ABC与△ A′B′C′相似吗?你用什么方法来支持你的判断?
C
B
A
A′
B′
C′
解:这两个三角形相似.
设1个小方格的边长为1,则
3.如图,△ABC中,点D、E、F分别是AB、BC、CA的中点,求证:△ABC∽△EFD.
∴△ABC∽△EFD.
证明:∵△ABC中,点D、E、F分别是AB、BC、CA的中点,
三边成比例的两个三角形相似
利用三边判定两个三角形相似
相似三角形的判定定理的运用
课堂小结
今日作业
课本第42页习题27.2第1,2(1),3(2)题
第二十七章 相 似
27.2.1 相似三角形的判定
第3课时 两边成比例且夹角相等的两个三角形相似
1.探索“两边成比例且夹角相等的两个角形相似”的判定定理;
2.会根据边和角的关系来判定两个三角形相似.(重点、难点)
问题1 我们学习过哪些判定三角形全等的方法?
问题2 我们目前知道的两个三角形相似有哪些判定方法?
回顾与思考
探 究 2
如图,在△ABC与△A′B′C′中,已知∠A= ∠A′
我们来证明一下前面得出的结论:
△A′B′C′∽△ABC.
B
A
C
D
E
B'
A'
C'
在△A′B′C′的边A′B′上截取点D,使A′D=AB.过点D作DE∥B′C′,交A′C′于点E.
∵DE∥B′C′,
∴△A′DE∽△A′B′C′.
∵A′D=AB,
∴A′E=AC. 又∠A′=∠A.
∴△A′DE≌△ABC,
∴△A′B′C′∽△ABC.
由此得到三角形的判定定理:
两边成比例且夹角相等的两个三角形相似.
归纳
例1 在△ABC和△DEF中,∠C=∠F=70°,AC=3.5cm,
BC=2.5 cm,DF=2.1 cm,EF=1.5 cm.求证:△DEF∽△ABC.
A
F
E
C
B
D
证明:
∵AC=3.5cm,BC=2.5cm,DF=2.1cm,EF=1.5cm,
又∵∠C=∠F=70°,
∴ △DEF∽△ABC(两边成比例且夹角相等的两个三角形相似)
典例精析
?如图,△ABC与△ADE都是等腰三角形,AD=AE,
AB=AC,∠DAB=∠CAE.求证:△ABC∽△ADE.
△ABC∽△ADE.
证明:
练一练
3.2
3.2
2
1.6
50°
)
如果两个三角形的两边成比例,但相等的角不是这两边的夹角,那么两个三角形是否相似呢?画一画,量一量.
探究归纳
两边成比例且夹角相等的两个三角形相似
利用两边及夹角判定三角形相似
相似三角形的判定定理的运用
课堂小结
今日作业
课本第42页习题27.2第2(2),3(2),4题
