人教版数学七年级上册 4.2.3线段的性质课件(共18张ppt)
文档属性
| 名称 | 人教版数学七年级上册 4.2.3线段的性质课件(共18张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 292.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-03 09:30:41 | ||
图片预览


文档简介
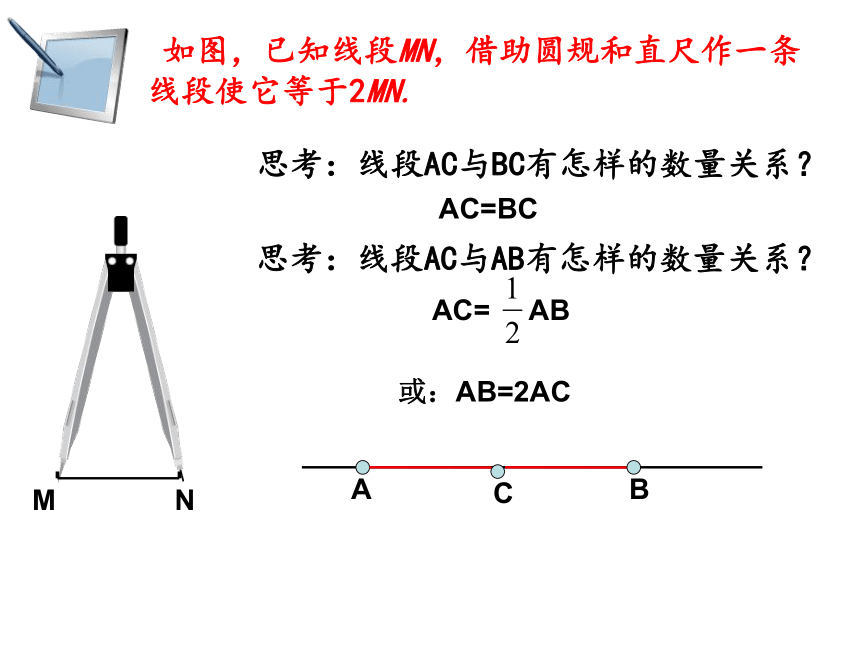
知识回顾
1、如图
AB= + ;
AC= - ;
2、如图
AC= + = - ;
BC= - = - ;
AC
BC
AB
BC
AB
BC
AD
CD
AC
AB
BD
CD
线段的中点
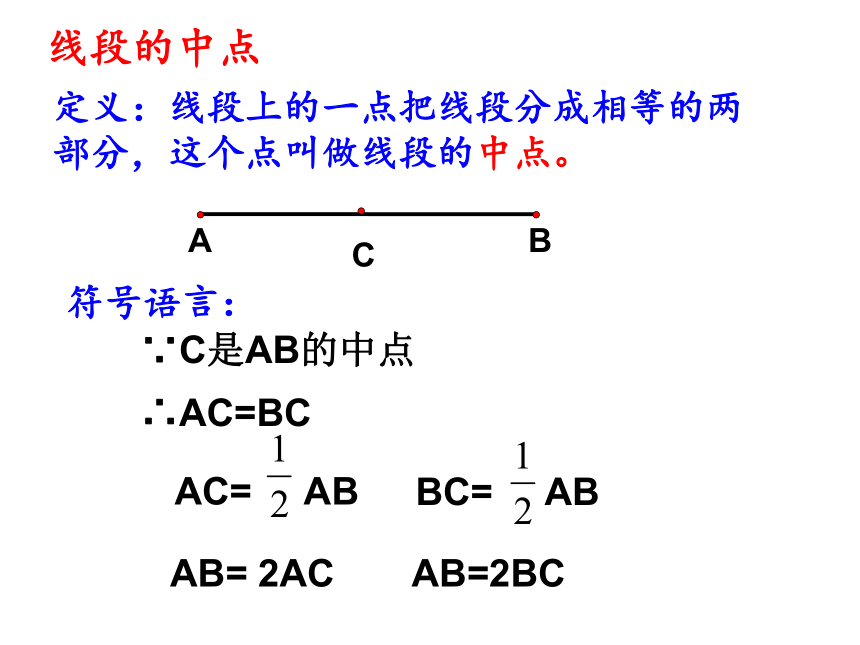
如图,已知线段MN,借助圆规和直尺作一条线段使它等于2MN.
A
C
B
思考:线段AC与BC有怎样的数量关系?
AC=BC
M
N
思考:线段AC与AB有怎样的数量关系?
AC= AB
或:AB=2AC
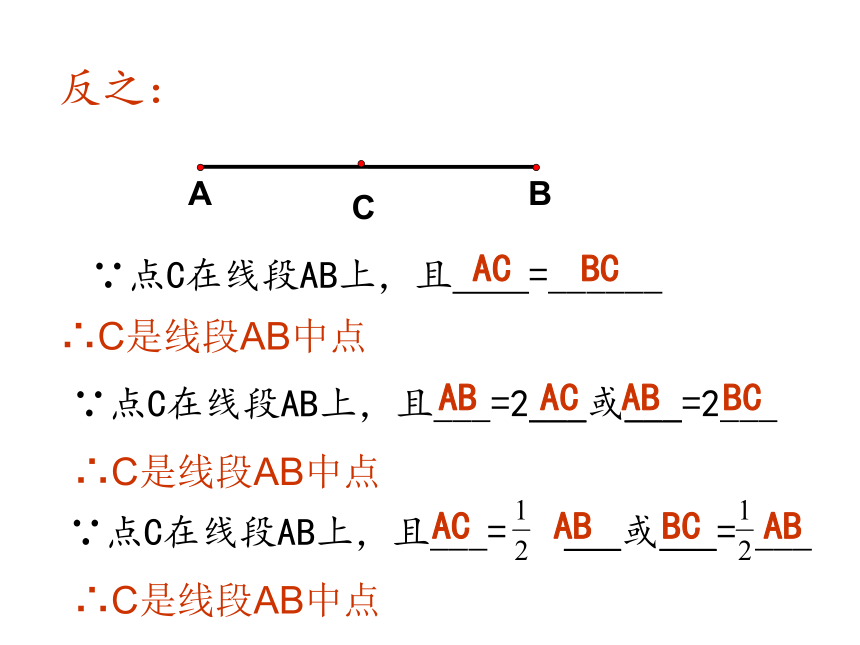
定义:
符号语言:
定义:线段上的一点把线段分成相等的两部分,这个点叫做线段的中点。
线段的中点
∴AC=BC
AC= AB
AB=2BC
C
A
B
BC= AB
AB= 2AC
∵C是AB的中点
∵点C在线段AB上,且 =______
定义:
C
A
B
反之:
AC
BC
∵点C在线段AB上,且___=2___或___=2___
AB
AB
AC
BC
∵点C在线段AB上,且___= ___或___= ___
AB
AB
AC
BC
∴C是线段AB中点
∴C是线段AB中点
∴C是线段AB中点
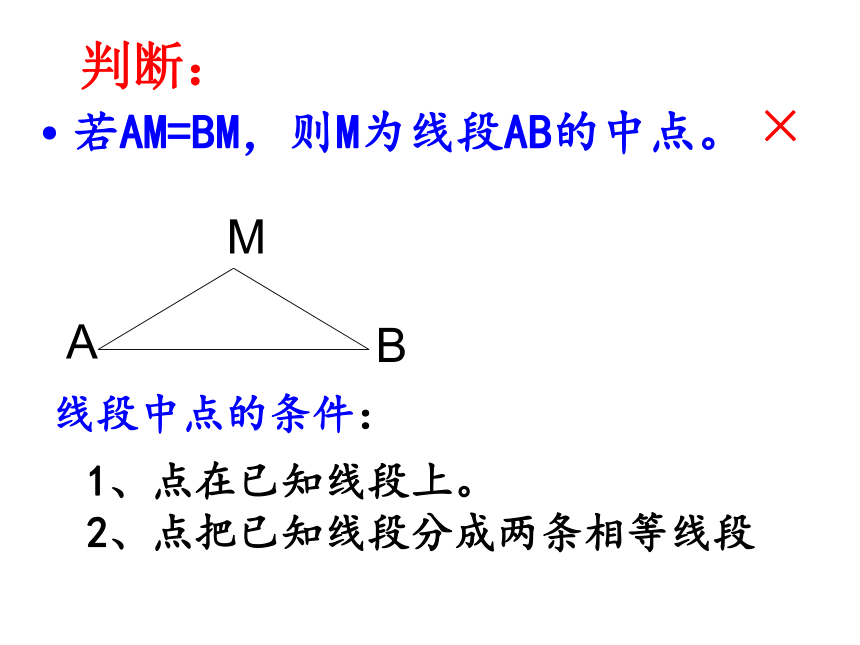
判断:
若AM=BM,则M为线段AB的中点。
线段中点的条件:
A
B
M
1、点在已知线段上。
2、点把已知线段分成两条相等线段
×
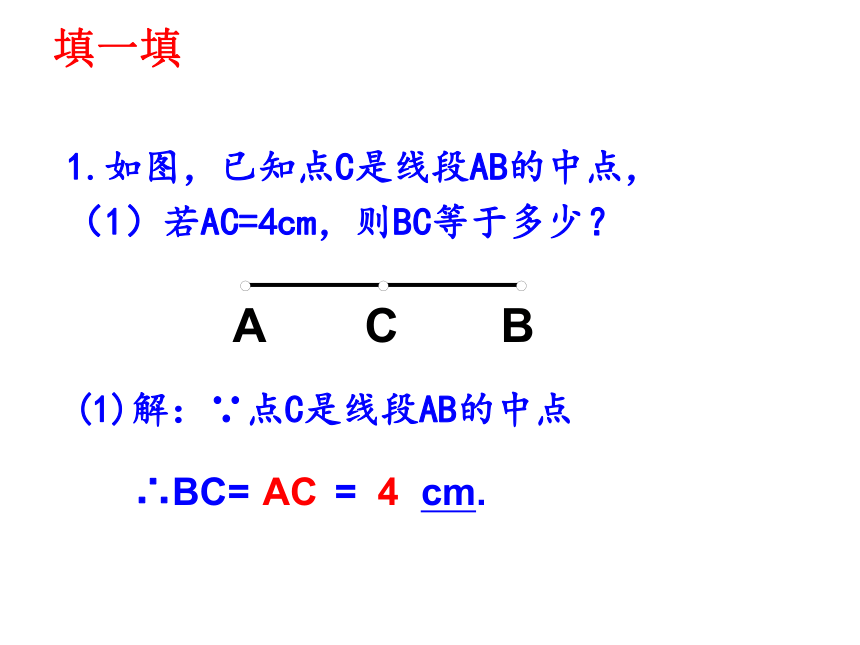
1.如图,已知点C是线段AB的中点,
(1)若AC=4cm,则BC等于多少?
填一填
(1)解:∵点C是线段AB的中点
∴BC= = cm.
AC
4
1.如图,已知点C是线段AB的中点,
(2)若AB=12cm,则BC等于多少?
填一填
(2)解∵点C是线段AB的中点
∴BC= AB.
∵AB=12cm
∴BC= .
1.如图,已知点C是线段AB的中点,
(3)若BC=3cm,则AB是多少?
填一填
(3)解∵点C是线段AB的中点
∴AB= BC
∵BC=3cm
∴AB= .
2
例、已知:AD=4cm,BD=2cm,点C是AB的中点,
求 ①BC长度.
② AC长度
③ CD长度
∵AB=AD+BD
又∵AD=4cm,BD=2cm
∴AB=4+2=6cm
∵C是AB的中点
∴
解:①
②
∵C是AB的中点
∴AC=BC=3cm
③
∵CD=BC- BD
∴CD=3 – 2=1cm
或∵CD=AD -AC
∴CD=4– 3=1cm
练习、已知AD=9cm,BD=3cm,C为AD的中点,E是BD的中点,求线段CE的长。
A
C
D
B
E
练习:点C是线段AB的中点,点D是线段AC的中点,若AB=4CM,求线段CD、DB的长度。
例:直线a上有A、B、C三点,且AB=8cm,BC=5cm,求线段AC的长。
C
a
(1)当C点在线段AB的延长线上时
(2)当C点在线段AB上时
a
A
B
C
例题讲解
B
A
例题:已知线段AB=12cm,直线AB上有一点C,且BC=6cm,M是线段AC的中点,求线段AM的长。
A
B
C
M
A
B
C
M
我有哪些收获呢?
与大家共分享!
回顾一下,我想说…
课堂小结
回顾一下,我想说…
? 线段的中点定义.
? 线段的符号语言.
? 线段中点的应用.
? 数形结合思想
数学知识:
数学思想:
学以致用
2.如图,已知点C是线段AB的中点,若AB=6cm,则BC= ,AC= .
1、如图,下列说法 ,不能判断点C是线段AB的中点的是( )
A、AC=CB B、AB=2AC
C、AC+CB=AB D、CB= AB
C
3cm
3cm
练习
3、已知线段AB = 4cm,延长AB到C,使BC = 2AB,若D为AB的中点,则线段DC 的长为 cm。
A
B
C
D
4cm
8cm
2cm
2cm + 8cm = 10cm
10
1、如图
AB= + ;
AC= - ;
2、如图
AC= + = - ;
BC= - = - ;
AC
BC
AB
BC
AB
BC
AD
CD
AC
AB
BD
CD
线段的中点
如图,已知线段MN,借助圆规和直尺作一条线段使它等于2MN.
A
C
B
思考:线段AC与BC有怎样的数量关系?
AC=BC
M
N
思考:线段AC与AB有怎样的数量关系?
AC= AB
或:AB=2AC
定义:
符号语言:
定义:线段上的一点把线段分成相等的两部分,这个点叫做线段的中点。
线段的中点
∴AC=BC
AC= AB
AB=2BC
C
A
B
BC= AB
AB= 2AC
∵C是AB的中点
∵点C在线段AB上,且 =______
定义:
C
A
B
反之:
AC
BC
∵点C在线段AB上,且___=2___或___=2___
AB
AB
AC
BC
∵点C在线段AB上,且___= ___或___= ___
AB
AB
AC
BC
∴C是线段AB中点
∴C是线段AB中点
∴C是线段AB中点
判断:
若AM=BM,则M为线段AB的中点。
线段中点的条件:
A
B
M
1、点在已知线段上。
2、点把已知线段分成两条相等线段
×
1.如图,已知点C是线段AB的中点,
(1)若AC=4cm,则BC等于多少?
填一填
(1)解:∵点C是线段AB的中点
∴BC= = cm.
AC
4
1.如图,已知点C是线段AB的中点,
(2)若AB=12cm,则BC等于多少?
填一填
(2)解∵点C是线段AB的中点
∴BC= AB.
∵AB=12cm
∴BC= .
1.如图,已知点C是线段AB的中点,
(3)若BC=3cm,则AB是多少?
填一填
(3)解∵点C是线段AB的中点
∴AB= BC
∵BC=3cm
∴AB= .
2
例、已知:AD=4cm,BD=2cm,点C是AB的中点,
求 ①BC长度.
② AC长度
③ CD长度
∵AB=AD+BD
又∵AD=4cm,BD=2cm
∴AB=4+2=6cm
∵C是AB的中点
∴
解:①
②
∵C是AB的中点
∴AC=BC=3cm
③
∵CD=BC- BD
∴CD=3 – 2=1cm
或∵CD=AD -AC
∴CD=4– 3=1cm
练习、已知AD=9cm,BD=3cm,C为AD的中点,E是BD的中点,求线段CE的长。
A
C
D
B
E
练习:点C是线段AB的中点,点D是线段AC的中点,若AB=4CM,求线段CD、DB的长度。
例:直线a上有A、B、C三点,且AB=8cm,BC=5cm,求线段AC的长。
C
a
(1)当C点在线段AB的延长线上时
(2)当C点在线段AB上时
a
A
B
C
例题讲解
B
A
例题:已知线段AB=12cm,直线AB上有一点C,且BC=6cm,M是线段AC的中点,求线段AM的长。
A
B
C
M
A
B
C
M
我有哪些收获呢?
与大家共分享!
回顾一下,我想说…
课堂小结
回顾一下,我想说…
? 线段的中点定义.
? 线段的符号语言.
? 线段中点的应用.
? 数形结合思想
数学知识:
数学思想:
学以致用
2.如图,已知点C是线段AB的中点,若AB=6cm,则BC= ,AC= .
1、如图,下列说法 ,不能判断点C是线段AB的中点的是( )
A、AC=CB B、AB=2AC
C、AC+CB=AB D、CB= AB
C
3cm
3cm
练习
3、已知线段AB = 4cm,延长AB到C,使BC = 2AB,若D为AB的中点,则线段DC 的长为 cm。
A
B
C
D
4cm
8cm
2cm
2cm + 8cm = 10cm
10
