人教版(五四制)七年级数学上册 第13章 实数 单元检测试题(Word版 含解析)
文档属性
| 名称 | 人教版(五四制)七年级数学上册 第13章 实数 单元检测试题(Word版 含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 33.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-03 00:00:00 | ||
图片预览



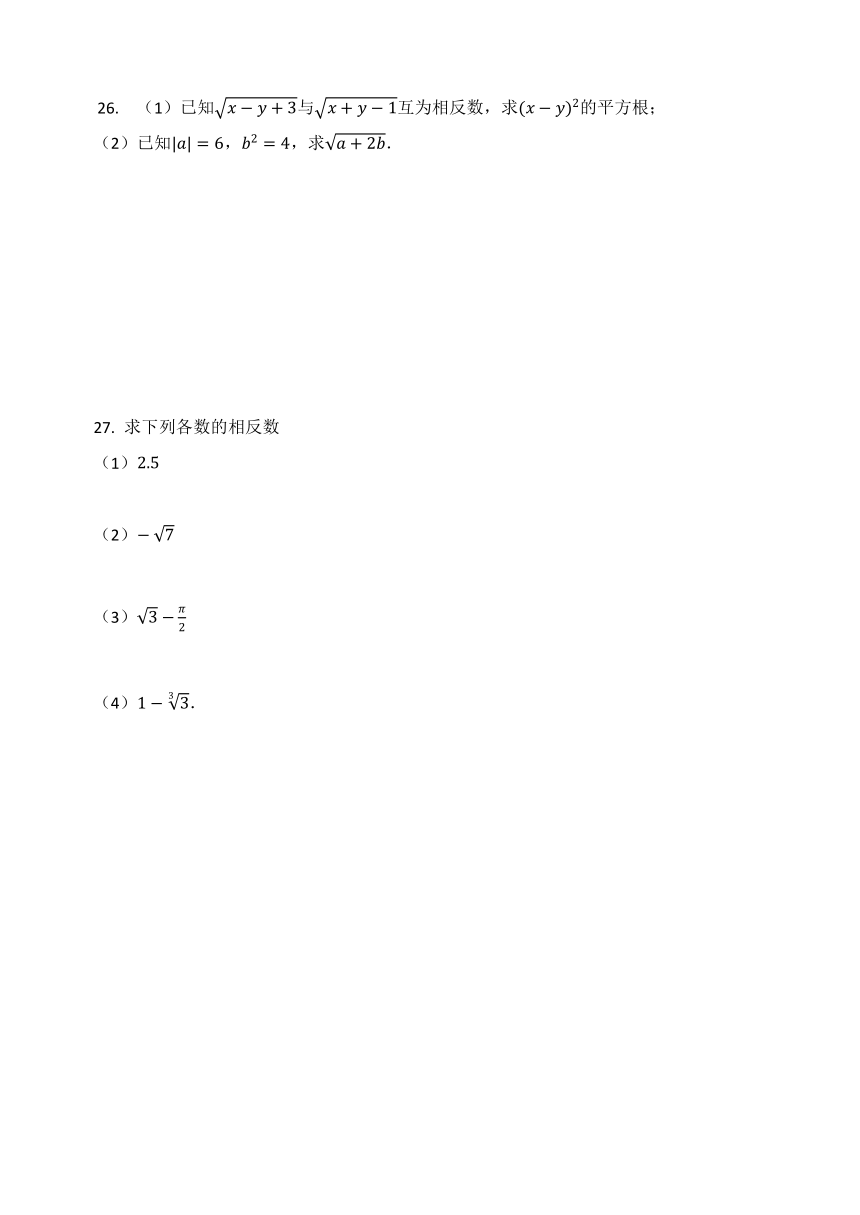

文档简介
第13章
实数
单元检测试题
(满分120分;时间:120分钟)
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?
1.
的平方根等于(?
?
?
?
)
A.
B.
C.
D.
?
2.
立方根等于本身的数是
A.,
B.
C.,
D.,
?
3.
计算的平方根为(
)
A.
B.
C.
D.
?
4.
下列各数中最小的是(
)
A.
B.
C.
D.
?
5.
已知,则的值为?
?
?
?
A.
B.
C.
D.
?
6.
下列各式中正确的是(
)
A.
B.
C.
D.
?
7.
已知,则
A.
B.
C.
D.
?
8.
估算的值(
)
A.在和之间
B.在和之间
C.在和之间
D.在和之间?
9.
的立方根与的平方根之和为(
)
A.
B.
C.或
D.或
?
10.
用“&”定义新运算:对于任意实数,都有&;,如果&&,那么等于(
)
A.
B.
C.
D.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?
11.
请写出一个负无理数________.
?
12.
比较大小________.
?
13.
若与是同一个数的平方根,则为________.
?
14.
若一正数的平方根分别是和,则这个正数是________.
?
15.
大于且小于的所有整数是_________.
?
16.
已知的算术平方根是,则的平方根是________.
?
17.
的相反数是________,的倒数是________.
?
18.
若,则在数轴上原点的________侧.
?
19.
若一个正数的两个平方根是和,则这个数是________.
?
20.
将,,按从小大的顺序排列________.
三、
解答题
(本题共计
7
小题,共计60分
,
)
?
21.
写出大于的所有负整数.
?
22.
已知,满足,求的值.
?
23.
估计的大小等于多少(误差小于).
?
24.
计算:.
?
25.
把下列数填入相应的集合中.
,.
整数集合(?
?
?
?
);
分数集合(?
?
?
?
);
有理数集合(?
?
?
?
);
无理数集合(?
?
?
?
);
实数集合(?
?
?
?
).
?26.
(1)已知与互为相反数,求的平方根;
(2)已知,,求.
27.
求下列各数的相反数
(1)???
(2)
(3)
(4).
参考答案
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
1.
【答案】
B
【解答】
解:∵
,,
∴
的平方根是.
故选.
2.
【答案】
A
【解答】
解:,,.
故选.
3.
【答案】
B
【解答】
解:∵
,
又∵
,
∴
的平方根是,即的平方根.
故选.
4.
【答案】
A
【解答】
解:根据实数比较大小的方法,可得
,
∴
各数中最小的是.
故选:.
5.
【答案】
A
【解答】
解:要使有意义,则
解得,
故,
∴
.
故选.
6.
【答案】
D
【解答】
.原式,不符合题意;
.原式,不符合题意;
.原式不能化简,不符合题意;
.原式,符合题意,
故选.
7.
【答案】
C
【解答】
解:∵
,
∴
.
故选.
8.
【答案】
C
【解答】
解:∵
,
∴
.
故选.
9.
【答案】
C
【解答】
解:∵
的立方根为,的平方根,
∴
的立方根与的平方根之和为或.
故选
10.
【答案】
C
【解答】
解:∵
&;,
∴
&&&&,
∴
.
故选.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
)
11.
【答案】
(答案不唯一)
【解答】
由无理数的定义可知,、是负无理数.
12.
【答案】
【解答】
解:∵
,
∴
,
故答案为:.
13.
【答案】
或
【解答】
解:依题意得:或,
解得或,
∴
的值为或.
故答案为:或.
14.
【答案】
【解答】
根据题意得:=,即=,
则这个正数为=.
15.
【答案】
【解答】
解:,,
,
符合题意得所有整数有.
故答案为:.
16.
【答案】
【解答】
由题意知=,
则=,
=,
=,
∴
==,
则,即的平方根是,
17.
【答案】
,
【解答】
的相反数是,倒数是.
18.
【答案】
左
【解答】
解:∵
,
∴
,
即在数轴上原点的左侧,
故答案为:左.
19.
【答案】
【解答】
解:∵
一个正数的两个平方根是和,
∴
.
解得:.
∴
.
∵
,
∴
这个正数为.
故答案为:.
20.
【答案】
【解答】
解:,,,
∵
,
∴
将,,按从小大的顺序排列.
故答案为:.
三、
解答题
(本题共计
7
小题
,每题
10
分
,共计70分
)
21.
【答案】
解:写出大于的所有负整数,,,.
【解答】
解:写出大于的所有负整数,,,.
22.
【答案】
解:由题意得,,,
则,
解得,,
则,
当,时,原式.
【解答】
解:由题意得,,,
则,
解得,,
则,
当,时,原式.
23.
【答案】
解:∵
,,
∴
.
【解答】
解:∵
,,
∴
.
24.
【答案】
解:原式
.
【解答】
解:原式
.
25.
【答案】
,.
,
【解答】
解:,
则是整数.
故答案为:.
是分数.
故答案为:.
∵
有理数就是有限的数,
,是有理数.
故答案为:,.
∵
无理数是无限的数,
是无理数.
故答案为:.
,是实数.
故答案为;,.
26.
【答案】
解:(1)∵
与互为相反数,
∴
,
解得:,
∴
的平方根是,
(2)∵
,,
∴
,,
∴
,或,
∵
,
∴
,或.
【解答】
解:(1)∵
与互为相反数,
∴
,
解得:,
∴
的平方根是,
(2)∵
,,
∴
,,
∴
,或,
∵
,
∴
,或.
27.
【答案】
解:(1)的相反数是;???
(2)的相反数是;
(3)的相反数是;
(4)的相反数是.
【解答】
解:(1)的相反数是;???
(2)的相反数是;
(3)的相反数是;
(4)的相反数是.
.
实数
单元检测试题
(满分120分;时间:120分钟)
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?
1.
的平方根等于(?
?
?
?
)
A.
B.
C.
D.
?
2.
立方根等于本身的数是
A.,
B.
C.,
D.,
?
3.
计算的平方根为(
)
A.
B.
C.
D.
?
4.
下列各数中最小的是(
)
A.
B.
C.
D.
?
5.
已知,则的值为?
?
?
?
A.
B.
C.
D.
?
6.
下列各式中正确的是(
)
A.
B.
C.
D.
?
7.
已知,则
A.
B.
C.
D.
?
8.
估算的值(
)
A.在和之间
B.在和之间
C.在和之间
D.在和之间?
9.
的立方根与的平方根之和为(
)
A.
B.
C.或
D.或
?
10.
用“&”定义新运算:对于任意实数,都有&;,如果&&,那么等于(
)
A.
B.
C.
D.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?
11.
请写出一个负无理数________.
?
12.
比较大小________.
?
13.
若与是同一个数的平方根,则为________.
?
14.
若一正数的平方根分别是和,则这个正数是________.
?
15.
大于且小于的所有整数是_________.
?
16.
已知的算术平方根是,则的平方根是________.
?
17.
的相反数是________,的倒数是________.
?
18.
若,则在数轴上原点的________侧.
?
19.
若一个正数的两个平方根是和,则这个数是________.
?
20.
将,,按从小大的顺序排列________.
三、
解答题
(本题共计
7
小题,共计60分
,
)
?
21.
写出大于的所有负整数.
?
22.
已知,满足,求的值.
?
23.
估计的大小等于多少(误差小于).
?
24.
计算:.
?
25.
把下列数填入相应的集合中.
,.
整数集合(?
?
?
?
);
分数集合(?
?
?
?
);
有理数集合(?
?
?
?
);
无理数集合(?
?
?
?
);
实数集合(?
?
?
?
).
?26.
(1)已知与互为相反数,求的平方根;
(2)已知,,求.
27.
求下列各数的相反数
(1)???
(2)
(3)
(4).
参考答案
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
1.
【答案】
B
【解答】
解:∵
,,
∴
的平方根是.
故选.
2.
【答案】
A
【解答】
解:,,.
故选.
3.
【答案】
B
【解答】
解:∵
,
又∵
,
∴
的平方根是,即的平方根.
故选.
4.
【答案】
A
【解答】
解:根据实数比较大小的方法,可得
,
∴
各数中最小的是.
故选:.
5.
【答案】
A
【解答】
解:要使有意义,则
解得,
故,
∴
.
故选.
6.
【答案】
D
【解答】
.原式,不符合题意;
.原式,不符合题意;
.原式不能化简,不符合题意;
.原式,符合题意,
故选.
7.
【答案】
C
【解答】
解:∵
,
∴
.
故选.
8.
【答案】
C
【解答】
解:∵
,
∴
.
故选.
9.
【答案】
C
【解答】
解:∵
的立方根为,的平方根,
∴
的立方根与的平方根之和为或.
故选
10.
【答案】
C
【解答】
解:∵
&;,
∴
&&&&,
∴
.
故选.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
)
11.
【答案】
(答案不唯一)
【解答】
由无理数的定义可知,、是负无理数.
12.
【答案】
【解答】
解:∵
,
∴
,
故答案为:.
13.
【答案】
或
【解答】
解:依题意得:或,
解得或,
∴
的值为或.
故答案为:或.
14.
【答案】
【解答】
根据题意得:=,即=,
则这个正数为=.
15.
【答案】
【解答】
解:,,
,
符合题意得所有整数有.
故答案为:.
16.
【答案】
【解答】
由题意知=,
则=,
=,
=,
∴
==,
则,即的平方根是,
17.
【答案】
,
【解答】
的相反数是,倒数是.
18.
【答案】
左
【解答】
解:∵
,
∴
,
即在数轴上原点的左侧,
故答案为:左.
19.
【答案】
【解答】
解:∵
一个正数的两个平方根是和,
∴
.
解得:.
∴
.
∵
,
∴
这个正数为.
故答案为:.
20.
【答案】
【解答】
解:,,,
∵
,
∴
将,,按从小大的顺序排列.
故答案为:.
三、
解答题
(本题共计
7
小题
,每题
10
分
,共计70分
)
21.
【答案】
解:写出大于的所有负整数,,,.
【解答】
解:写出大于的所有负整数,,,.
22.
【答案】
解:由题意得,,,
则,
解得,,
则,
当,时,原式.
【解答】
解:由题意得,,,
则,
解得,,
则,
当,时,原式.
23.
【答案】
解:∵
,,
∴
.
【解答】
解:∵
,,
∴
.
24.
【答案】
解:原式
.
【解答】
解:原式
.
25.
【答案】
,.
,
【解答】
解:,
则是整数.
故答案为:.
是分数.
故答案为:.
∵
有理数就是有限的数,
,是有理数.
故答案为:,.
∵
无理数是无限的数,
是无理数.
故答案为:.
,是实数.
故答案为;,.
26.
【答案】
解:(1)∵
与互为相反数,
∴
,
解得:,
∴
的平方根是,
(2)∵
,,
∴
,,
∴
,或,
∵
,
∴
,或.
【解答】
解:(1)∵
与互为相反数,
∴
,
解得:,
∴
的平方根是,
(2)∵
,,
∴
,,
∴
,或,
∵
,
∴
,或.
27.
【答案】
解:(1)的相反数是;???
(2)的相反数是;
(3)的相反数是;
(4)的相反数是.
【解答】
解:(1)的相反数是;???
(2)的相反数是;
(3)的相反数是;
(4)的相反数是.
.
