北师大版数学九年级上册课件:4.5 相似三角形判定定理的证明(共16张PPT)
文档属性
| 名称 | 北师大版数学九年级上册课件:4.5 相似三角形判定定理的证明(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 329.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-03 00:00:00 | ||
图片预览



文档简介
(共16张PPT)
相似三角形判定定理的证明
第四章
图形的相似
知识点1 相似三角形的判定定理
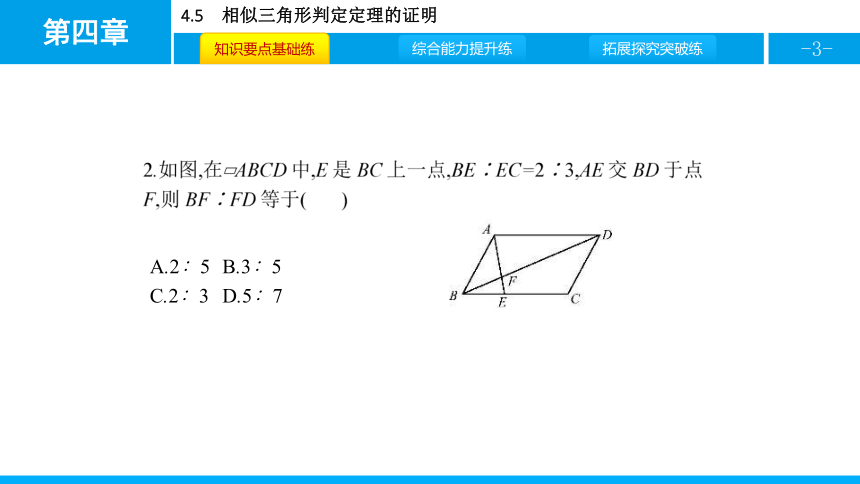
1.如图,在△ABC中,∠ACB=90°,如果CD⊥AB于点D,那么(
C
)
A.2∶5
B.3∶5
C.2∶3
D.5∶7
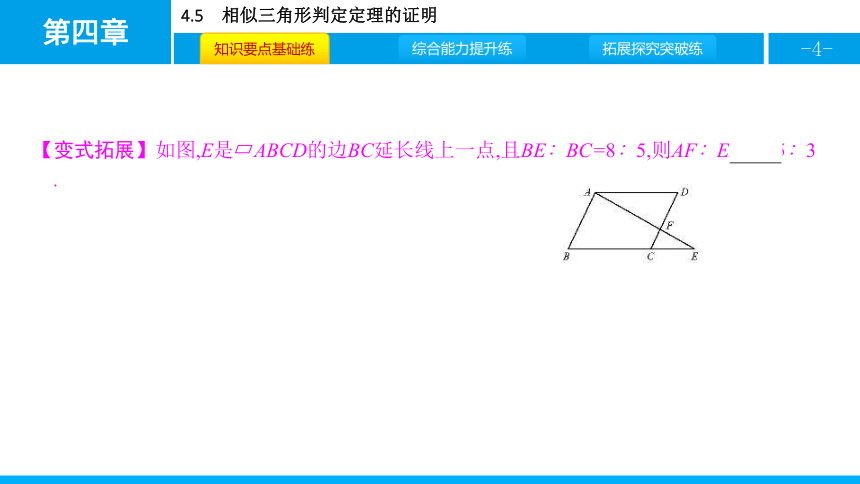
【变式拓展】如图,E是?ABCD的边BC延长线上一点,且BE∶BC=8∶5,则AF∶EF= 5∶3 .?
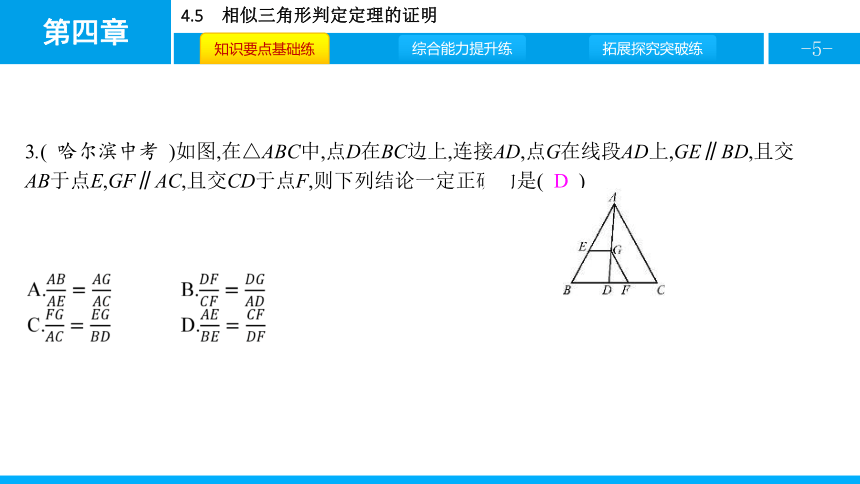
3.(
哈尔滨中考
)如图,在△ABC中,点D在BC边上,连接AD,点G在线段AD上,GE∥BD,且交AB于点E,GF∥AC,且交CD于点F,则下列结论一定正确的是(
D
)
知识点2 相似三角形判定定理的综合应用
4.如图,为了测量一池塘的宽DE,在岸边找到一点C,测得CD=30
m,在DC的延长线上找到一点A,测得AC=5
m,过点A作AB∥DE交EC的延长线于点B,测出AB=6
m,则池塘的宽DE为(
C
)
A.25
m
B.30
m
C.36
m
D.40
m
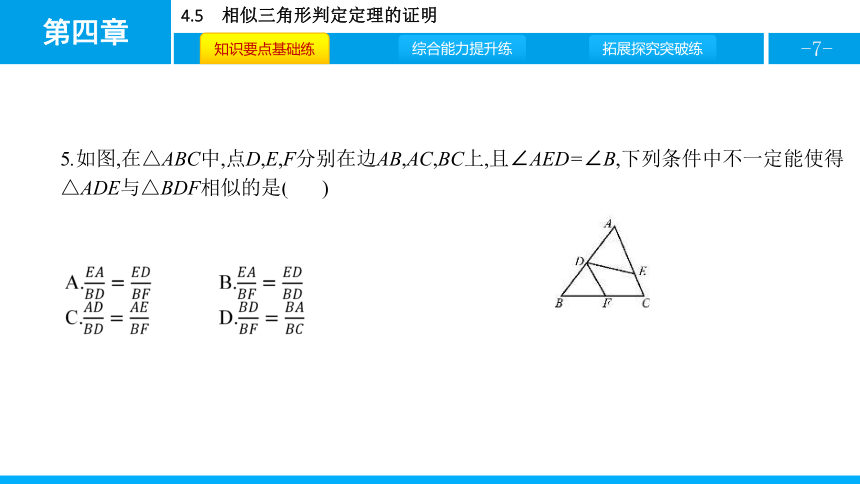
5.如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,且∠AED=∠B,下列条件中不一定能使得△ADE与△BDF相似的是(
C
)
6.(
教材母题变式
)在△ABC中,边BC=6,高AD=4,正方形EFGH的顶点E,F在边BC上,顶点H,G分别在边AB和AC上,求这个正方形的边长.
解:如图所示,∵四边形EFGH是正方形,
7.(
梧州中考
)如图,AG∶GD=4∶1,BD∶DC=2∶3,则AE∶EC的值是(
D
)
A.3∶2
B.4∶3
C.6∶5
D.8∶5
9.如图,在四边形ABCD中,对角线AC与BD相交于点O,AC平分∠DAB,且∠DAC=∠DBC,那么下列结论不一定正确的是(
D
)
A.△AOD∽△BOC
B.△AOB∽△DOC
C.CD=BC
D.BC·CD=AC·OA
10.如图,在方格纸中,△ABC和△EPD的顶点均在格点上,要使△ABC∽△EPD,则点P所在的格点为 P3 .?
11.如图,四边形ABCD是正方形,E是CD的中点,P是BC边上的一点,请你补充一个条件,当 BP=2PC(
答案不唯一
) 时,能够使△ABP与△ECP相似.?
12.如图,在边长为1的正方形ABCD中,E是AB的中点,CF⊥DE,F为垂足.
(
1
)△CDF与△DEA是否相似?请说明理由.
(
2
)求CF的长.
13.如图,已知△ABC,△DEF均为等边三角形,点D,E分别在AB,BC上.
(
1
)图中有哪些相似三角形?请把它们表示出来.
(
2
)请找一个与△BDE相似的三角形并说明理由.
解:(
1
)相似三角形有:△ABC∽△DEF,△AGD∽△BDE∽△CEH∽△FGH.
(
2
)△AGD∽△BDE.
理由:略.
14.如图,在菱形ABCD中,P是对角线AC上的一点,连接DP并延长交AB于点E,交CB的延长线于点F.若DP=3,EF=2,则PE的长是(
B
)
相似三角形判定定理的证明
第四章
图形的相似
知识点1 相似三角形的判定定理
1.如图,在△ABC中,∠ACB=90°,如果CD⊥AB于点D,那么(
C
)
A.2∶5
B.3∶5
C.2∶3
D.5∶7
【变式拓展】如图,E是?ABCD的边BC延长线上一点,且BE∶BC=8∶5,则AF∶EF= 5∶3 .?
3.(
哈尔滨中考
)如图,在△ABC中,点D在BC边上,连接AD,点G在线段AD上,GE∥BD,且交AB于点E,GF∥AC,且交CD于点F,则下列结论一定正确的是(
D
)
知识点2 相似三角形判定定理的综合应用
4.如图,为了测量一池塘的宽DE,在岸边找到一点C,测得CD=30
m,在DC的延长线上找到一点A,测得AC=5
m,过点A作AB∥DE交EC的延长线于点B,测出AB=6
m,则池塘的宽DE为(
C
)
A.25
m
B.30
m
C.36
m
D.40
m
5.如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,且∠AED=∠B,下列条件中不一定能使得△ADE与△BDF相似的是(
C
)
6.(
教材母题变式
)在△ABC中,边BC=6,高AD=4,正方形EFGH的顶点E,F在边BC上,顶点H,G分别在边AB和AC上,求这个正方形的边长.
解:如图所示,∵四边形EFGH是正方形,
7.(
梧州中考
)如图,AG∶GD=4∶1,BD∶DC=2∶3,则AE∶EC的值是(
D
)
A.3∶2
B.4∶3
C.6∶5
D.8∶5
9.如图,在四边形ABCD中,对角线AC与BD相交于点O,AC平分∠DAB,且∠DAC=∠DBC,那么下列结论不一定正确的是(
D
)
A.△AOD∽△BOC
B.△AOB∽△DOC
C.CD=BC
D.BC·CD=AC·OA
10.如图,在方格纸中,△ABC和△EPD的顶点均在格点上,要使△ABC∽△EPD,则点P所在的格点为 P3 .?
11.如图,四边形ABCD是正方形,E是CD的中点,P是BC边上的一点,请你补充一个条件,当 BP=2PC(
答案不唯一
) 时,能够使△ABP与△ECP相似.?
12.如图,在边长为1的正方形ABCD中,E是AB的中点,CF⊥DE,F为垂足.
(
1
)△CDF与△DEA是否相似?请说明理由.
(
2
)求CF的长.
13.如图,已知△ABC,△DEF均为等边三角形,点D,E分别在AB,BC上.
(
1
)图中有哪些相似三角形?请把它们表示出来.
(
2
)请找一个与△BDE相似的三角形并说明理由.
解:(
1
)相似三角形有:△ABC∽△DEF,△AGD∽△BDE∽△CEH∽△FGH.
(
2
)△AGD∽△BDE.
理由:略.
14.如图,在菱形ABCD中,P是对角线AC上的一点,连接DP并延长交AB于点E,交CB的延长线于点F.若DP=3,EF=2,则PE的长是(
B
)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
