华师大版 九年级下册数学 27.3圆中的计算问题 同步习题(Word版 含解析)
文档属性
| 名称 | 华师大版 九年级下册数学 27.3圆中的计算问题 同步习题(Word版 含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 287.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-03 08:59:58 | ||
图片预览



文档简介
27.3圆中的计算问题
同步习题
一.选择题
1.如图,从一块半径为20cm的圆形铁皮上剪出一个圆心角是60°的扇形ABC,则此扇形围成的圆锥的侧面积为( )
A.200πcm2
B.100πcm2
C.100πcm2
D.50πcm2
2.如图,在等腰直角三角形ABC中,∠C=90°,AB=4,以A为圆心,AC长为半径作弧,交AB于点D,则阴影部分的面积是( )
A.2π
B.8
C.8﹣2π
D.16﹣2π
3.如图,在Rt△ABC中,∠ABC=90°,以BC的中点O为圆心,OB的长为半径作半圆交AC于点D,若AD=1,DC=3,则图中阴影部分的面积为( )
A.
B.
C.
D.3π﹣2
4.将某圆锥形的冰淇淋纸套沿它的一条母线展开若不考虑接缝,它是一个半径为12cm,圆心角为120o的扇形,则( )
A.圆锥形冰淇淋纸套的底面半径为8cm
B.圆锥形冰淇淋纸套的底面半径为6cm
C.圆锥形冰淇淋纸套的高为
D.圆锥形冰淇淋纸套的高为
5.如图,边长为4的正方形ABCD外切于圆O,则阴影部分面积为( )
A.2π﹣4
B.2π+4
C.15
D.14
6.如图,正方形ABCD的边长为4,以点A为圆心,AD为半径,画圆弧DE得到扇形DAE(阴影部分,点E在对角线AC上).若扇形DAE正好是一个圆锥的侧面展开图,则该圆锥的底面圆的半径是( )
A.
B.1
C.
D.
7.如图,已知点C,D是以AB为直径的半圆的三等分点,弧CD的长为π,则图中阴影部分的面积为( )
A.π
B.π
C.π
D.π+
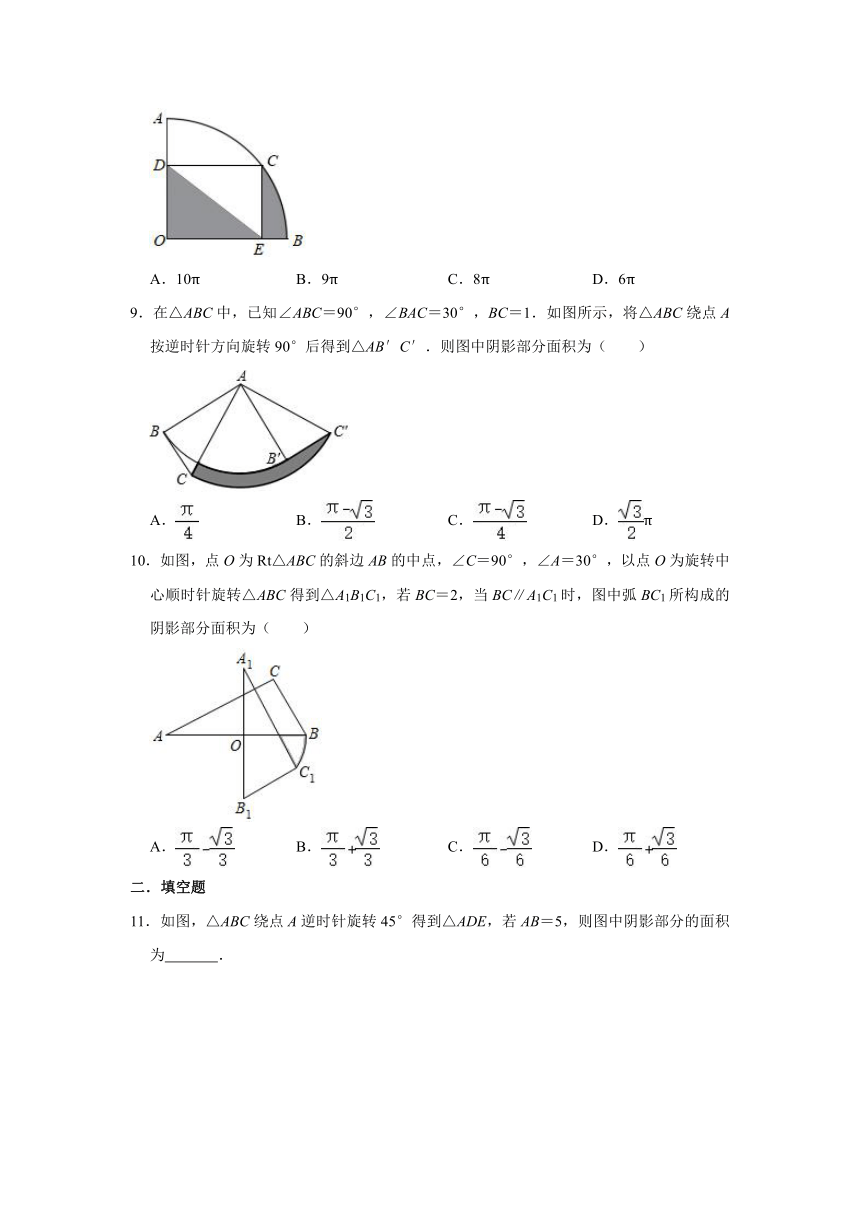
8.如图,半径为10的扇形AOB中,∠AOB=90°,C为上一点,CD⊥OA,CE⊥OB,垂足分别为D、E.若∠CDE为36°,则图中阴影部分的面积为( )
A.10π
B.9π
C.8π
D.6π
9.在△ABC中,已知∠ABC=90°,∠BAC=30°,BC=1.如图所示,将△ABC绕点A按逆时针方向旋转90°后得到△AB′C′.则图中阴影部分面积为( )
A.
B.
C.
D.π
10.如图,点O为Rt△ABC的斜边AB的中点,∠C=90°,∠A=30°,以点O为旋转中心顺时针旋转△ABC得到△A1B1C1,若BC=2,当BC∥A1C1时,图中弧BC1所构成的阴影部分面积为( )
A.
B.
C.
D.
二.填空题
11.如图,△ABC绕点A逆时针旋转45°得到△ADE,若AB=5,则图中阴影部分的面积为
.
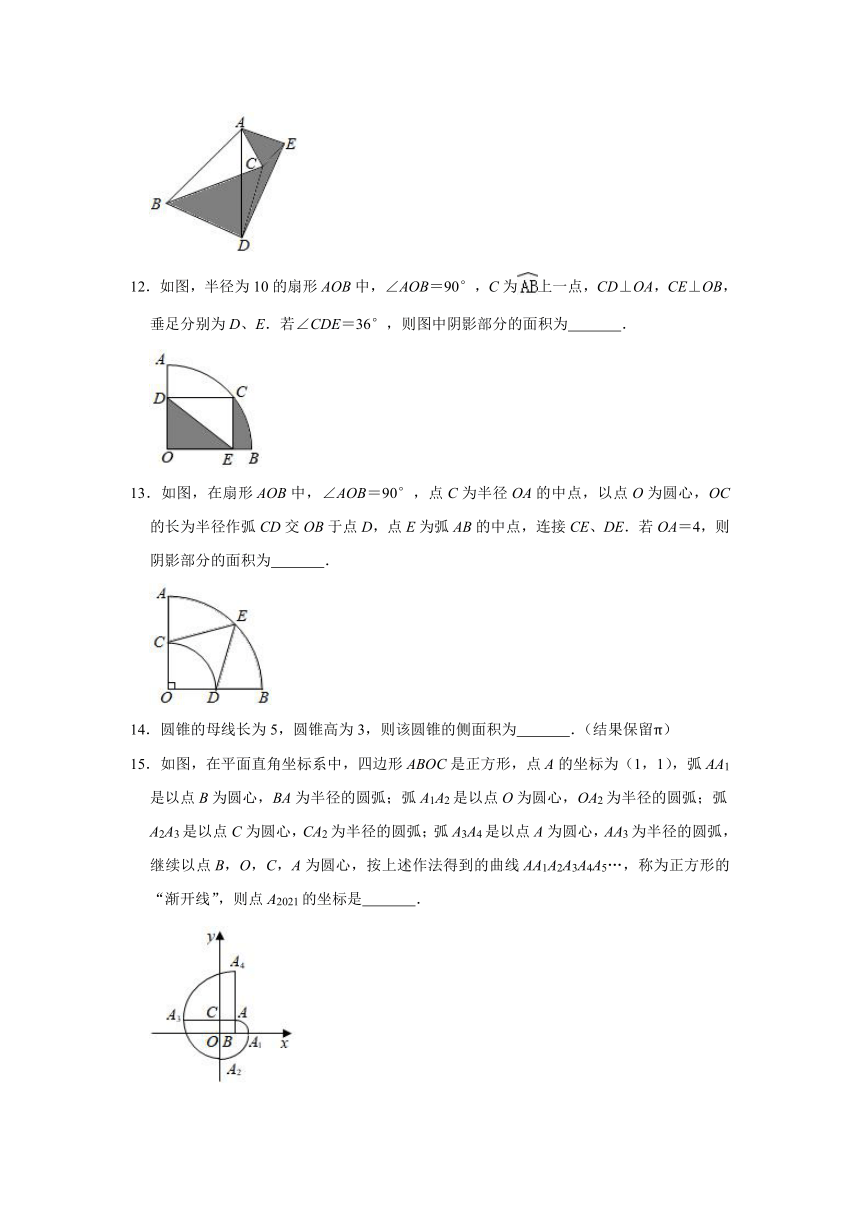
12.如图,半径为10的扇形AOB中,∠AOB=90°,C为上一点,CD⊥OA,CE⊥OB,垂足分别为D、E.若∠CDE=36°,则图中阴影部分的面积为
.
13.如图,在扇形AOB中,∠AOB=90°,点C为半径OA的中点,以点O为圆心,OC的长为半径作弧CD交OB于点D,点E为弧AB的中点,连接CE、DE.若OA=4,则阴影部分的面积为
.
14.圆锥的母线长为5,圆锥高为3,则该圆锥的侧面积为
.(结果保留π)
15.如图,在平面直角坐标系中,四边形ABOC是正方形,点A的坐标为(1,1),弧AA1是以点B为圆心,BA为半径的圆弧;弧A1A2是以点O为圆心,OA2为半径的圆弧;弧A2A3是以点C为圆心,CA2为半径的圆弧;弧A3A4是以点A为圆心,AA3为半径的圆弧,继续以点B,O,C,A为圆心,按上述作法得到的曲线AA1A2A3A4A5…,称为正方形的“渐开线”,则点A2021的坐标是
.
三.解答题
16.如图,扇形OAB的半径OA=4,圆心角∠AOB=90°,点C是弧AB上异于A、B的一点,过点C作CD⊥OA于点D,作CE⊥OB于点E,连结DE,过点C作弧AB所在圆的切线CG交OA的延长线于点G.
(1)求证:∠CGO=∠CDE;
(2)若∠CGD=60°,求图中阴影部分的面积.
17.如图,已知AB,CD为⊙O的直径,过点A作弦AE垂直于直径CD于F,点B恰好为的中点,连接BC,BE.
(1)求证:AE=BC;
(2)若AE=2,求⊙O的半径;
(3)在(2)的条件下,求阴影部分的面积.
18.矩形ABCD的一边长AB=4,且BC>AB,以边AB为直径的圆O交对角线AC于H,AH=2.如图,点K为优弧AKB上一点.
(Ⅰ)求∠HKA的度数;
(Ⅱ)求CH的长;
(Ⅲ)求图中阴影部分的面积;
(Ⅳ)设AK=m,若圆O的圆周上到直线AK的距离为1的点有且仅有三个,求实数m的值.
参考答案
一.选择题
1.解:作OD⊥AB于D,如图,则AD=BD,
∵∠OAD=∠BAC=30°,
∴OD=OA=10,AD=OD=10,
∴AB=2AD=20,
∴扇形围成的圆锥的侧面积==200π(cm2).
故选:A.
2.解:∵△ACB是等腰直角三角形,∠ACB=90°,
∴∠A=∠B=45°,
∵AB=4,
∴AC=BC=AB×sin45°=4,
∴S△ACB==8,S扇形ACD==2π,
∴图中阴影部分的面积是8﹣2π.
故选:C.
3.解:连接OD、BD、作DE⊥BC于点E,
∵BC是⊙O的直径,
∴∠BDC=90°,
∴∠DBC+∠BCD=90°,
∵∠ABC=90°,
∴∠A+∠BCD=90°,
∴∠A=∠DBC,
又∵∠ADB=∠BDC,
∴△ADB∽△BDC,
∴,
∵AD=1,DC=3,
∴,
∴BD=,
∴BC==2,
∴∠DCB=30°,OD=OC=,
∴∠DOC=120°,
∵DE⊥BC,
∴DE=1.5,
∴阴影部分的面积是:=π﹣=,
故选:A.
4.解:半径为12cm,圆心角为120°的扇形弧长是:(cm)
设圆锥的底面半径是r(cm)
则:2πr=8π,解得:r=4
即个圆淋的底面半径是4cm;
圆锥形冰淇淋纸套的高为=8(cm).
故选:C.
5.解:如图,连接HO,延长HO交BC于点P,
∵正方形ABCD外切于⊙O,
∴∠A=∠B=∠AHP=90°,
∴四边形AHPB为矩形,
∴∠OPB=90°,
又∠OFB=90°,
∴点P与点F重合
则HF为⊙O的直径,
同理EG为⊙O的直径,
由∠D=∠OGD=∠OHD=90°且OH=OG知,四边形BGOH为正方形,
同理四边形OGCF、四边形OFBE、四边形OEAH均为正方形,
∴DH=DG=GC=CF=2,∠HGO=∠FGO=45°,
∴∠HGF=90°,GH=GF===2,
则阴影部分面积=S⊙O+S△HGF
=?π?22+×2×2
=2π+4,
故选:B.
6.解:设圆锥的底面圆的半径为r,
根据题意可知:
AD=AE=4,∠DAE=45°,
底面圆的周长等于弧长:
∴2πr=,
解得r=.
答:该圆锥的底面圆的半径是.
故选:D.
7.解:连接CD、OC、OD.
∵C,D是以AB为直径的半圆的三等分点,
∴∠AOC=∠COD=∠DOB=60°,AC=CD,
又∵OA=OC=OD,
∴△OAC、△OCD是等边三角形,
∴∠AOC=∠OCD,
∴CD∥AB,
∴S△ACD=S△OCD,
∵弧CD的长为,
∴=,
解得:r=1,
∴S阴影=S扇形OCD==.
故选:A.
8.解:连接OC,
∵∠AOB=90°,CD⊥OA,CE⊥OB,
∴四边形CDOE是矩形,
∴CD∥OE,
∴∠DEO=∠CDE=36°,
由矩形CDOE易得到△DOE≌△CEO,
∴∠COB=∠DEO=36°
∴图中阴影部分的面积=扇形OBC的面积,
∵S扇形OBC==10π
∴图中阴影部分的面积=10π,
故选:A.
9.解:∵∠ABC=90°,∠BAC=30°,BC=1,
∴AB=BC=,AC=2BC=2,
∴图中阴影部分面积=﹣﹣=,
故选:B.
10.解:设A1C1与AB的交点为D,连接OC1,作DE⊥OC1于E,
∵在△ABC中,∠C=90°,∠A=30°,BC=2,
∴AB=2BC=4,∠ABC=60°,
∵点O为Rt△ABC的斜边AB的中点,
∴OC=AB=2,
∴OC1=OA1=2,
∴∠A1=∠A1C1O=30°,
∴∠A1OC1=120°,
∵BC∥A1C1,
∴∠ADA1=∠ABC=60°,
∵∠A1=∠A=30°,
∴∠A1OD=90°,
∴∠DOC1=30°,
∴∠DOC1=∠A1C1O,
∴OD=DC1,
∴OE=EC1=1,
∴DE=OE=,
∴S阴影=S扇形﹣S=﹣=﹣,
故选:A.
二.填空题
11.解:作DM⊥AB于M,
∵△ABC绕点A逆时针旋转45°得到△ADE,AB=5,
∴△AED的面积=△ABC的面积,∠BAD=45°,AB=AD=5,
∴DM=AD=,
∴S△ABD==×=,
∵图中阴影部分的面积=△AED的面积+△ADB的面积﹣△ABC的面积=△ADB的面积,
∴S阴影=,
故答案为:.
12.解:连接OC,
∵∠AOB=90°,CD⊥OA,CE⊥OB,
∴四边形CDOE是矩形,
∴CD∥OE,
∴∠DEO=∠CDE=36°,
由矩形CDOE易得到△DOE≌△CEO,
∴∠COB=∠DEO=36°
∴图中阴影部分的面积=扇形OBC的面积,
∵S扇形OBC==10π
∴图中阴影部分的面积=10π,
故答案为10π.
13.解:如图,连接AB,CD,OE,OE交CD于J.
∵OC=AC,OD=DB,
∴CD∥AB,
∵=,
∴OE⊥AB,
∴CD⊥OE,
∵OC=OD=2,
∴CJ=OJ,
∵∠COD=90°,
∴CD===2,
∴S四边形OCED=?CD?OE=4,
∴S阴=S扇形AOB﹣S四边形OCED=?π?42﹣4=4π﹣4,
故答案为:4π﹣4.
14.解:圆锥的底面圆的半径为=4,
所以该圆锥的侧面积=×2π×4×5=20π.
故答案为20π.
15.解:A(1,1),
由题意得,A1(2,0),A2(0,﹣2),A3(﹣3,1),A4(1,5),
A5(6,0),A6(0,﹣6),A7(﹣7,1),A8(1,9)…,
∴A4n(1,4n+1),A4n+1(4n+2,0),A4n+2(0,﹣(4n+2)),A4n+3(﹣(4n+3),1).
∵2021=505×4+1,
∴A2021的坐标为(2022,0).
故答案为:(2022,0).
三.解答题
16.解:(1)连接OC交DE于F,
∵CD⊥OA,CE⊥OB,
∴∠CEO=∠AOB=∠CDO=90°,
∴四边形CEOD是矩形,
∴CG=DF=EF=OF,∠ECD=90°,
∴∠FCD=∠CDF,∠ECF+∠FCD=90°,
∵CG是⊙O的切线,
∴∠OCG=90°,
∴∠OCD+∠GCD=90°,
∴∠ECF=∠GCD,
∵∠DCG+∠CGD=90°,
∴∠FCD=∠CGD,
∴∠CGO=∠CDE;
(2)由(1)知,∠CGD=∠CDE=60°,
∴∠DCO=60°,
∴∠COD=30°,
∵OC=OA=4,
∴CD=2,OD=2,
∴图中阴影部分的面积=﹣2×2=π﹣2.
17.(1)证明:连接BD,
∵AB,CD为⊙O的直径,
∴∠CBD=∠AEB=90°,
∵点B恰好为的中点,
∴=,
∴∠A=∠C,
∵∠ABE=90°﹣∠A,∠CDB=90°﹣∠C,
∴∠ABE=∠CDB,
∴=,
∴AE=BC;
(2)解:∵过点A作弦AE垂直于直径CD于F,
∴=,
∵=,
∴==,
∴∠A=∠ABE,
∴∠A=30°,
在Rt△ABE中,cos∠A=,
∴AB===4,
∴⊙O的半径为2.
(3)连接OE,
∵∠A=30°,
∴∠EOB=60°,
∴△EOB是等边三角形,
∵OB=OE=2,
∴S△EOB=×2×=,
∴S阴=S扇形﹣S△EOB=﹣=﹣.
18.解:(Ⅰ)连接BH,
∵AB为⊙O的直径,
∴∠AHB=90°,
∵AB=4,AH=2,
∴sin∠ABH===,
∴∠ABH=30°,
∴∠HKA=∠ABH=30°;
(Ⅱ)∵∠AHB=90°,∠ABH=30°,
∴∠BAH=60°,
∵四边形ABCD是矩形,
∴∠ABC=90°,
∴AC=2AB=8,
∴CH=AC﹣AH=6;
(Ⅲ)连接OH,则△AOH是等边三角形,
∴AO=AH=2,∠AOH=60°,
过H作HE⊥AO于E,则HE=,
∵AC=8,CD=AB=4,
∴AD=4,
∴图中阴影部分的面积=×44﹣(﹣×2×)=9﹣π;
(Ⅳ)过O作平行于AK的直线交⊙O于MN,过O作OP⊥AK于Q交⊙O于P,
∵⊙O的半径=2,则PQ=OQ=1,
∵OA=2,
∴AQ=,
∴AK=2AQ=2,
∴m=2.
同步习题
一.选择题
1.如图,从一块半径为20cm的圆形铁皮上剪出一个圆心角是60°的扇形ABC,则此扇形围成的圆锥的侧面积为( )
A.200πcm2
B.100πcm2
C.100πcm2
D.50πcm2
2.如图,在等腰直角三角形ABC中,∠C=90°,AB=4,以A为圆心,AC长为半径作弧,交AB于点D,则阴影部分的面积是( )
A.2π
B.8
C.8﹣2π
D.16﹣2π
3.如图,在Rt△ABC中,∠ABC=90°,以BC的中点O为圆心,OB的长为半径作半圆交AC于点D,若AD=1,DC=3,则图中阴影部分的面积为( )
A.
B.
C.
D.3π﹣2
4.将某圆锥形的冰淇淋纸套沿它的一条母线展开若不考虑接缝,它是一个半径为12cm,圆心角为120o的扇形,则( )
A.圆锥形冰淇淋纸套的底面半径为8cm
B.圆锥形冰淇淋纸套的底面半径为6cm
C.圆锥形冰淇淋纸套的高为
D.圆锥形冰淇淋纸套的高为
5.如图,边长为4的正方形ABCD外切于圆O,则阴影部分面积为( )
A.2π﹣4
B.2π+4
C.15
D.14
6.如图,正方形ABCD的边长为4,以点A为圆心,AD为半径,画圆弧DE得到扇形DAE(阴影部分,点E在对角线AC上).若扇形DAE正好是一个圆锥的侧面展开图,则该圆锥的底面圆的半径是( )
A.
B.1
C.
D.
7.如图,已知点C,D是以AB为直径的半圆的三等分点,弧CD的长为π,则图中阴影部分的面积为( )
A.π
B.π
C.π
D.π+
8.如图,半径为10的扇形AOB中,∠AOB=90°,C为上一点,CD⊥OA,CE⊥OB,垂足分别为D、E.若∠CDE为36°,则图中阴影部分的面积为( )
A.10π
B.9π
C.8π
D.6π
9.在△ABC中,已知∠ABC=90°,∠BAC=30°,BC=1.如图所示,将△ABC绕点A按逆时针方向旋转90°后得到△AB′C′.则图中阴影部分面积为( )
A.
B.
C.
D.π
10.如图,点O为Rt△ABC的斜边AB的中点,∠C=90°,∠A=30°,以点O为旋转中心顺时针旋转△ABC得到△A1B1C1,若BC=2,当BC∥A1C1时,图中弧BC1所构成的阴影部分面积为( )
A.
B.
C.
D.
二.填空题
11.如图,△ABC绕点A逆时针旋转45°得到△ADE,若AB=5,则图中阴影部分的面积为
.
12.如图,半径为10的扇形AOB中,∠AOB=90°,C为上一点,CD⊥OA,CE⊥OB,垂足分别为D、E.若∠CDE=36°,则图中阴影部分的面积为
.
13.如图,在扇形AOB中,∠AOB=90°,点C为半径OA的中点,以点O为圆心,OC的长为半径作弧CD交OB于点D,点E为弧AB的中点,连接CE、DE.若OA=4,则阴影部分的面积为
.
14.圆锥的母线长为5,圆锥高为3,则该圆锥的侧面积为
.(结果保留π)
15.如图,在平面直角坐标系中,四边形ABOC是正方形,点A的坐标为(1,1),弧AA1是以点B为圆心,BA为半径的圆弧;弧A1A2是以点O为圆心,OA2为半径的圆弧;弧A2A3是以点C为圆心,CA2为半径的圆弧;弧A3A4是以点A为圆心,AA3为半径的圆弧,继续以点B,O,C,A为圆心,按上述作法得到的曲线AA1A2A3A4A5…,称为正方形的“渐开线”,则点A2021的坐标是
.
三.解答题
16.如图,扇形OAB的半径OA=4,圆心角∠AOB=90°,点C是弧AB上异于A、B的一点,过点C作CD⊥OA于点D,作CE⊥OB于点E,连结DE,过点C作弧AB所在圆的切线CG交OA的延长线于点G.
(1)求证:∠CGO=∠CDE;
(2)若∠CGD=60°,求图中阴影部分的面积.
17.如图,已知AB,CD为⊙O的直径,过点A作弦AE垂直于直径CD于F,点B恰好为的中点,连接BC,BE.
(1)求证:AE=BC;
(2)若AE=2,求⊙O的半径;
(3)在(2)的条件下,求阴影部分的面积.
18.矩形ABCD的一边长AB=4,且BC>AB,以边AB为直径的圆O交对角线AC于H,AH=2.如图,点K为优弧AKB上一点.
(Ⅰ)求∠HKA的度数;
(Ⅱ)求CH的长;
(Ⅲ)求图中阴影部分的面积;
(Ⅳ)设AK=m,若圆O的圆周上到直线AK的距离为1的点有且仅有三个,求实数m的值.
参考答案
一.选择题
1.解:作OD⊥AB于D,如图,则AD=BD,
∵∠OAD=∠BAC=30°,
∴OD=OA=10,AD=OD=10,
∴AB=2AD=20,
∴扇形围成的圆锥的侧面积==200π(cm2).
故选:A.
2.解:∵△ACB是等腰直角三角形,∠ACB=90°,
∴∠A=∠B=45°,
∵AB=4,
∴AC=BC=AB×sin45°=4,
∴S△ACB==8,S扇形ACD==2π,
∴图中阴影部分的面积是8﹣2π.
故选:C.
3.解:连接OD、BD、作DE⊥BC于点E,
∵BC是⊙O的直径,
∴∠BDC=90°,
∴∠DBC+∠BCD=90°,
∵∠ABC=90°,
∴∠A+∠BCD=90°,
∴∠A=∠DBC,
又∵∠ADB=∠BDC,
∴△ADB∽△BDC,
∴,
∵AD=1,DC=3,
∴,
∴BD=,
∴BC==2,
∴∠DCB=30°,OD=OC=,
∴∠DOC=120°,
∵DE⊥BC,
∴DE=1.5,
∴阴影部分的面积是:=π﹣=,
故选:A.
4.解:半径为12cm,圆心角为120°的扇形弧长是:(cm)
设圆锥的底面半径是r(cm)
则:2πr=8π,解得:r=4
即个圆淋的底面半径是4cm;
圆锥形冰淇淋纸套的高为=8(cm).
故选:C.
5.解:如图,连接HO,延长HO交BC于点P,
∵正方形ABCD外切于⊙O,
∴∠A=∠B=∠AHP=90°,
∴四边形AHPB为矩形,
∴∠OPB=90°,
又∠OFB=90°,
∴点P与点F重合
则HF为⊙O的直径,
同理EG为⊙O的直径,
由∠D=∠OGD=∠OHD=90°且OH=OG知,四边形BGOH为正方形,
同理四边形OGCF、四边形OFBE、四边形OEAH均为正方形,
∴DH=DG=GC=CF=2,∠HGO=∠FGO=45°,
∴∠HGF=90°,GH=GF===2,
则阴影部分面积=S⊙O+S△HGF
=?π?22+×2×2
=2π+4,
故选:B.
6.解:设圆锥的底面圆的半径为r,
根据题意可知:
AD=AE=4,∠DAE=45°,
底面圆的周长等于弧长:
∴2πr=,
解得r=.
答:该圆锥的底面圆的半径是.
故选:D.
7.解:连接CD、OC、OD.
∵C,D是以AB为直径的半圆的三等分点,
∴∠AOC=∠COD=∠DOB=60°,AC=CD,
又∵OA=OC=OD,
∴△OAC、△OCD是等边三角形,
∴∠AOC=∠OCD,
∴CD∥AB,
∴S△ACD=S△OCD,
∵弧CD的长为,
∴=,
解得:r=1,
∴S阴影=S扇形OCD==.
故选:A.
8.解:连接OC,
∵∠AOB=90°,CD⊥OA,CE⊥OB,
∴四边形CDOE是矩形,
∴CD∥OE,
∴∠DEO=∠CDE=36°,
由矩形CDOE易得到△DOE≌△CEO,
∴∠COB=∠DEO=36°
∴图中阴影部分的面积=扇形OBC的面积,
∵S扇形OBC==10π
∴图中阴影部分的面积=10π,
故选:A.
9.解:∵∠ABC=90°,∠BAC=30°,BC=1,
∴AB=BC=,AC=2BC=2,
∴图中阴影部分面积=﹣﹣=,
故选:B.
10.解:设A1C1与AB的交点为D,连接OC1,作DE⊥OC1于E,
∵在△ABC中,∠C=90°,∠A=30°,BC=2,
∴AB=2BC=4,∠ABC=60°,
∵点O为Rt△ABC的斜边AB的中点,
∴OC=AB=2,
∴OC1=OA1=2,
∴∠A1=∠A1C1O=30°,
∴∠A1OC1=120°,
∵BC∥A1C1,
∴∠ADA1=∠ABC=60°,
∵∠A1=∠A=30°,
∴∠A1OD=90°,
∴∠DOC1=30°,
∴∠DOC1=∠A1C1O,
∴OD=DC1,
∴OE=EC1=1,
∴DE=OE=,
∴S阴影=S扇形﹣S=﹣=﹣,
故选:A.
二.填空题
11.解:作DM⊥AB于M,
∵△ABC绕点A逆时针旋转45°得到△ADE,AB=5,
∴△AED的面积=△ABC的面积,∠BAD=45°,AB=AD=5,
∴DM=AD=,
∴S△ABD==×=,
∵图中阴影部分的面积=△AED的面积+△ADB的面积﹣△ABC的面积=△ADB的面积,
∴S阴影=,
故答案为:.
12.解:连接OC,
∵∠AOB=90°,CD⊥OA,CE⊥OB,
∴四边形CDOE是矩形,
∴CD∥OE,
∴∠DEO=∠CDE=36°,
由矩形CDOE易得到△DOE≌△CEO,
∴∠COB=∠DEO=36°
∴图中阴影部分的面积=扇形OBC的面积,
∵S扇形OBC==10π
∴图中阴影部分的面积=10π,
故答案为10π.
13.解:如图,连接AB,CD,OE,OE交CD于J.
∵OC=AC,OD=DB,
∴CD∥AB,
∵=,
∴OE⊥AB,
∴CD⊥OE,
∵OC=OD=2,
∴CJ=OJ,
∵∠COD=90°,
∴CD===2,
∴S四边形OCED=?CD?OE=4,
∴S阴=S扇形AOB﹣S四边形OCED=?π?42﹣4=4π﹣4,
故答案为:4π﹣4.
14.解:圆锥的底面圆的半径为=4,
所以该圆锥的侧面积=×2π×4×5=20π.
故答案为20π.
15.解:A(1,1),
由题意得,A1(2,0),A2(0,﹣2),A3(﹣3,1),A4(1,5),
A5(6,0),A6(0,﹣6),A7(﹣7,1),A8(1,9)…,
∴A4n(1,4n+1),A4n+1(4n+2,0),A4n+2(0,﹣(4n+2)),A4n+3(﹣(4n+3),1).
∵2021=505×4+1,
∴A2021的坐标为(2022,0).
故答案为:(2022,0).
三.解答题
16.解:(1)连接OC交DE于F,
∵CD⊥OA,CE⊥OB,
∴∠CEO=∠AOB=∠CDO=90°,
∴四边形CEOD是矩形,
∴CG=DF=EF=OF,∠ECD=90°,
∴∠FCD=∠CDF,∠ECF+∠FCD=90°,
∵CG是⊙O的切线,
∴∠OCG=90°,
∴∠OCD+∠GCD=90°,
∴∠ECF=∠GCD,
∵∠DCG+∠CGD=90°,
∴∠FCD=∠CGD,
∴∠CGO=∠CDE;
(2)由(1)知,∠CGD=∠CDE=60°,
∴∠DCO=60°,
∴∠COD=30°,
∵OC=OA=4,
∴CD=2,OD=2,
∴图中阴影部分的面积=﹣2×2=π﹣2.
17.(1)证明:连接BD,
∵AB,CD为⊙O的直径,
∴∠CBD=∠AEB=90°,
∵点B恰好为的中点,
∴=,
∴∠A=∠C,
∵∠ABE=90°﹣∠A,∠CDB=90°﹣∠C,
∴∠ABE=∠CDB,
∴=,
∴AE=BC;
(2)解:∵过点A作弦AE垂直于直径CD于F,
∴=,
∵=,
∴==,
∴∠A=∠ABE,
∴∠A=30°,
在Rt△ABE中,cos∠A=,
∴AB===4,
∴⊙O的半径为2.
(3)连接OE,
∵∠A=30°,
∴∠EOB=60°,
∴△EOB是等边三角形,
∵OB=OE=2,
∴S△EOB=×2×=,
∴S阴=S扇形﹣S△EOB=﹣=﹣.
18.解:(Ⅰ)连接BH,
∵AB为⊙O的直径,
∴∠AHB=90°,
∵AB=4,AH=2,
∴sin∠ABH===,
∴∠ABH=30°,
∴∠HKA=∠ABH=30°;
(Ⅱ)∵∠AHB=90°,∠ABH=30°,
∴∠BAH=60°,
∵四边形ABCD是矩形,
∴∠ABC=90°,
∴AC=2AB=8,
∴CH=AC﹣AH=6;
(Ⅲ)连接OH,则△AOH是等边三角形,
∴AO=AH=2,∠AOH=60°,
过H作HE⊥AO于E,则HE=,
∵AC=8,CD=AB=4,
∴AD=4,
∴图中阴影部分的面积=×44﹣(﹣×2×)=9﹣π;
(Ⅳ)过O作平行于AK的直线交⊙O于MN,过O作OP⊥AK于Q交⊙O于P,
∵⊙O的半径=2,则PQ=OQ=1,
∵OA=2,
∴AQ=,
∴AK=2AQ=2,
∴m=2.
