人教版七年级数学上册4.3: 角 教学案
文档属性
| 名称 | 人教版七年级数学上册4.3: 角 教学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 357.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-03 21:14:52 | ||
图片预览




文档简介
4.3
角
教学重难点
角的概念与表示方法;
角的比较与角的平分线的概念;
认识角的互余、互补关系及其性质。
要点1
角的度量与计算
例1:下面一些角中,可以用一副三角板画出来的角是
。
;(2);(3);(4);(5)
变式1:=
。
变式2:化成用度表示的形式为
。
变式3:计算:
(1);
(2);
(3);
(4)
要点2
与角平分线有关的计算
例2:(1)如图所示,,OM平分,ON平分,求的度数.
(2)如果(1)中,其他条件不变,求的度数.
(3)如果(1)中为锐角),其他条件不变,求的度数.
(4)从(1)(2)(3)的结果你能看出什么规律?
变式1:如图所示,OB是的角平分线,的度数为
。
变式2:如图,已知OB,OC是内部的两条射线,OM平分.
若的大小。
若(用含的式子表示)
要点3
余角和补角的概念及计算
例1:(1)如图1,点A,O,B在一条直线上,,若,则图中互余的角有
对。
如图2,O是直线AB上的一点,于点O,OE平分,则图中互补的角共有
对。
变式1:若一个角的余角等于它的补角的,则这个角的度数为
。
变式2:如图,已知互为补角,OD是的角平分线,OE在内,的度数。
要点4
角度计算中的分类讨论
例4:已知,过点O作射线OC(不同于OA,OB),满足的大小(题目中所说的角都是小于平角的角)
变式1:已知Z则的度数为
。
变式2:水平线上依次三点有A,O,B,以点O为顶点,在直线上方作,OM,ON分别平分的度数。
要点5
与角度计算有关的探究型问题
例5:如图1,O为直线AB上一点,过点O作射线OC,,将以直角三角板()的直角顶点放在点O处,一边ON在射线OA上,另一边OM与OC都在直线AB的上方。
将图1中的三角板绕点O以每秒的速度沿顺时针方向旋转一周。如图2,经过t秒后,OM恰好平分,①求t的值;②此时ON是否平分?请说明理由。
在第(1)题的基础上,若三角板在转动的同时,射线OC也绕点O以每秒的速度沿顺时针方向旋转一周,如图3,那么经过多长时间OC平分?请说明理由。
在第(2)题的基础上,经过多长时间OC平分?请画图并说明理由。
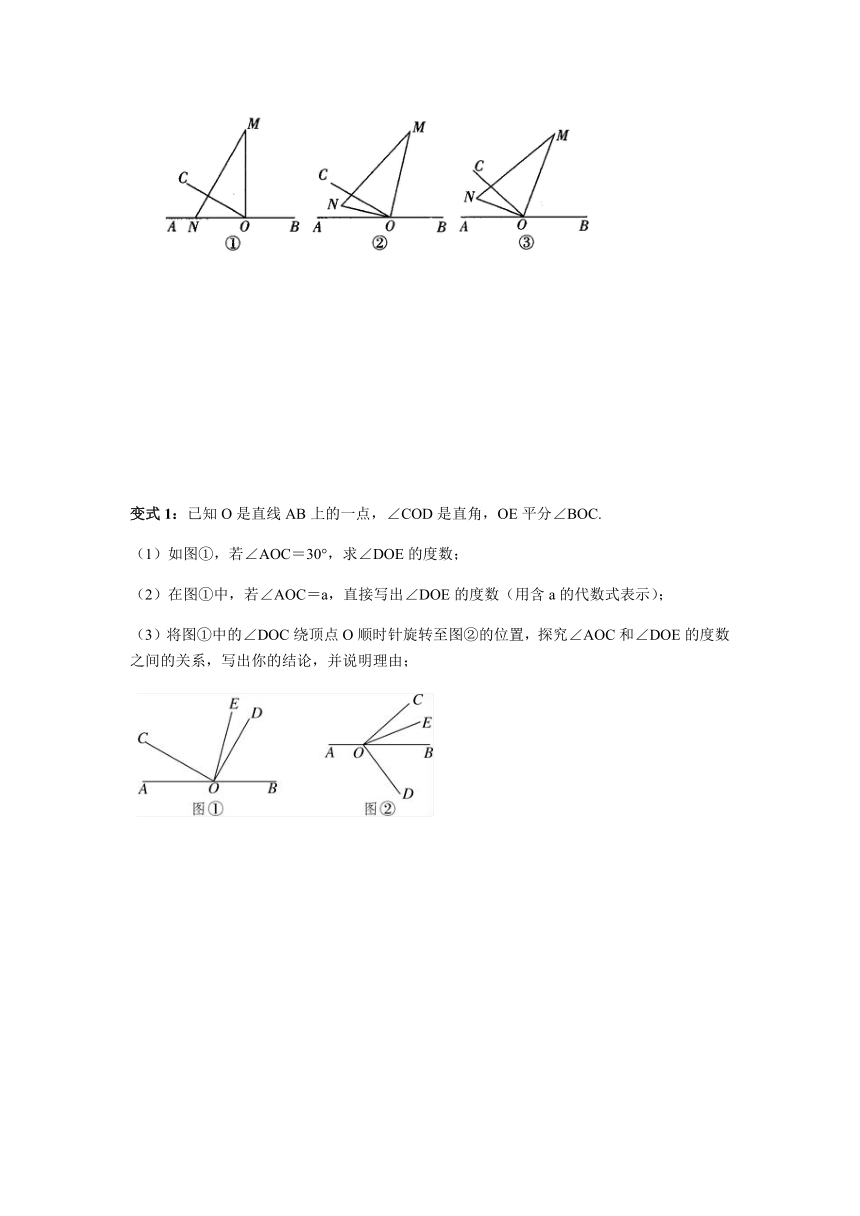
变式1:已知O是直线AB上的一点,∠COD是直角,OE平分∠BOC.
(1)如图①,若∠AOC=30°,求∠DOE的度数;
(2)在图①中,若∠AOC=a,直接写出∠DOE的度数(用含a的代数式表示);
(3)将图①中的∠DOC绕顶点O顺时针旋转至图②的位置,探究∠AOC和∠DOE的度数之间的关系,写出你的结论,并说明理由;
变式2:已知∠AOB=90°,∠COD=60°,OE平分∠AOC,OF平分∠BOD.
(1)如图1,当A、O、D三点共线时,则∠EOF=
;
(2)将∠COD绕点O顺时针方向旋转至如图2所示位置,∠COD的两边OC,OD都在∠AOB的内部,求∠EOF的度数;
(3)当∠COD旋转至如图3所示位置,作∠EOF的角平分线ON,求∠EON的度数。
要点6
有关钟表的角度问题
例6:在0时到12时之间,钟面上的时针与分针在什么时候成60
的角?试着尽可能多地找出答案.秒针与时针又共有多少次成的角?
变式1:钟表上12点15分时,时针和分针的夹角是
。
变式2:有一只手表每小时比准确时间慢3分钟,若在清晨4:30与准确时间对准,则当天上午手表指示的时间是10:50,准确时间应该是
。
变式3:某人下午6点多外出购物,表上的时针和分针的夹角恰为110°,下午近7点回家,发现表上的时针和分针的夹角又是110°,试算一算此人外出共用了多长时间?
变式4:时针在下午4点至5点的什么时刻:①分针和时针重合?②分针和时针成一条直线?③分针和时针成角?
巩
固
练
习
一、单选题
1.用两块角度分别为30°、60°、90°和45°、45°、90°的三角板画角,不可能画出的角是(
)
A.
125°
B.
105°
C.
75°
D.
15°
2.如图∠BCA=90,CD⊥AB,则图中互余的角有(
)对.
A.
1
B.
2
C.
3
D.
4
3.如图,一副三角尺按不同的位置摆放,摆放位置中的图形有
A.
1个
B.
2个
C.
3个
D.
4个
4.如右图所示正方形格中,连接,观测=(
)
A
.120°
B.
125°
C.130°
D.
135°
5.下列说法正确的是( )
A.
角的边越长,角度就越大
B.
周角就是一条射线
C.
一条直线可以看成平角
D.
平角的两边可以构成一条直线
6.将一副常规的三角尺按如图方式放置,则图中∠AOB的度数为(
)
A.
75?
B.
105?
C.
95?
D.
120?
7、如图,∠AOB是直角,OA平分∠COD,OE平分∠BOD,若∠BOE=23°,则∠BOC的度数是( )
A.113°
B.134°
C.136°
D.144°
8.一副三角板按如图所示的方式摆放,且∠1比∠2大50°,则∠2的度数为( )
A.
20°
B.
50°
C.
70°
D.
30°
9.∠AOB=45°,∠BOC=75°,OD平分∠AOB,OE平分∠BOC,则∠DOE=( )
A.
60°
B.
75°
C.
60°或15°
D.
70°或15°
10.已知:岛P位于岛Q的正西方,由岛P、Q分别测得船R位于南偏东30°和南偏西45°方向上,则符合条件的示意图是(
)
ABC.
D.
二、填空题
11.60.56°=______度_____分_____秒,28°28′12"=_________°;
12.一个锐角的余角是38°28′5′′,则这个角的补角是________.
13.八时三十分,时针与分针夹角度数是_______.
14.如图,点C在直线MN上,AC⊥BC于点C,∠1=65°,则∠2=____°源:
15.如图,O为直线AB上一点,OC平分∠AOD,∠AOC=53°17′,则∠BOD的度数为_____.
16.如图所示,O是直线AB上一点,OD平分∠BOC,
∠COE=90°,若∠AOC=40°,则∠DOE=_________.[]
三、解答题
17.计算:
(1)179°-72°18'54″;
(2)360°÷7(精确到秒).
18.已知一个角的补角比这个角的余角的4倍大15°,求这个角的度数。
19.如图,已知直线AB和CD相交于点O,∠COE=
90,
OF平分∠AOE,
∠COF=28.求∠AOC的度数.
20.如图,已知∠COB=3∠AOC,OD平分∠AOB,且∠AOB=120°,求∠COD的度数.
21.如图,将一副三角尺的直角顶点叠放在点C处,∠D=30°,∠B=45°,求:
(1)若∠DCE=35°,求∠ACB的度数;(2)若∠ACB=120°,求∠DCE的度数.
(3)猜想∠ACB和∠DCE的关系,并说明理由;
22.如图,∠AOB=115°,∠EOF
=155°,OA平分∠EOC,OB平分∠DOF,
(1)求∠AOE+∠FOB度数;
(2)求∠COD度数。
[]能力提升
23.点O为直线AB上一点,过点O作射线OC,使∠BOC=65°,将一直角三角板的直角顶点放在点O处.
[]
(1)如图1,将三角板MON的一边ON与射线OB重合时,则∠MOC=__________
(2)如图2,将三角板MON绕点O逆时针旋转一定角度,此时OC是∠MOB的平分线,求∠BON和∠CON的度数.
24.已知:如图,,.
(1)当时,=_________;[来源:学
科
网Z
X
X
K]
(2)当,时,_________;
(3)当,时,____________;
(4)猜想不论的度数是多少,的度数与的关系,并简述理由.
角
教学重难点
角的概念与表示方法;
角的比较与角的平分线的概念;
认识角的互余、互补关系及其性质。
要点1
角的度量与计算
例1:下面一些角中,可以用一副三角板画出来的角是
。
;(2);(3);(4);(5)
变式1:=
。
变式2:化成用度表示的形式为
。
变式3:计算:
(1);
(2);
(3);
(4)
要点2
与角平分线有关的计算
例2:(1)如图所示,,OM平分,ON平分,求的度数.
(2)如果(1)中,其他条件不变,求的度数.
(3)如果(1)中为锐角),其他条件不变,求的度数.
(4)从(1)(2)(3)的结果你能看出什么规律?
变式1:如图所示,OB是的角平分线,的度数为
。
变式2:如图,已知OB,OC是内部的两条射线,OM平分.
若的大小。
若(用含的式子表示)
要点3
余角和补角的概念及计算
例1:(1)如图1,点A,O,B在一条直线上,,若,则图中互余的角有
对。
如图2,O是直线AB上的一点,于点O,OE平分,则图中互补的角共有
对。
变式1:若一个角的余角等于它的补角的,则这个角的度数为
。
变式2:如图,已知互为补角,OD是的角平分线,OE在内,的度数。
要点4
角度计算中的分类讨论
例4:已知,过点O作射线OC(不同于OA,OB),满足的大小(题目中所说的角都是小于平角的角)
变式1:已知Z则的度数为
。
变式2:水平线上依次三点有A,O,B,以点O为顶点,在直线上方作,OM,ON分别平分的度数。
要点5
与角度计算有关的探究型问题
例5:如图1,O为直线AB上一点,过点O作射线OC,,将以直角三角板()的直角顶点放在点O处,一边ON在射线OA上,另一边OM与OC都在直线AB的上方。
将图1中的三角板绕点O以每秒的速度沿顺时针方向旋转一周。如图2,经过t秒后,OM恰好平分,①求t的值;②此时ON是否平分?请说明理由。
在第(1)题的基础上,若三角板在转动的同时,射线OC也绕点O以每秒的速度沿顺时针方向旋转一周,如图3,那么经过多长时间OC平分?请说明理由。
在第(2)题的基础上,经过多长时间OC平分?请画图并说明理由。
变式1:已知O是直线AB上的一点,∠COD是直角,OE平分∠BOC.
(1)如图①,若∠AOC=30°,求∠DOE的度数;
(2)在图①中,若∠AOC=a,直接写出∠DOE的度数(用含a的代数式表示);
(3)将图①中的∠DOC绕顶点O顺时针旋转至图②的位置,探究∠AOC和∠DOE的度数之间的关系,写出你的结论,并说明理由;
变式2:已知∠AOB=90°,∠COD=60°,OE平分∠AOC,OF平分∠BOD.
(1)如图1,当A、O、D三点共线时,则∠EOF=
;
(2)将∠COD绕点O顺时针方向旋转至如图2所示位置,∠COD的两边OC,OD都在∠AOB的内部,求∠EOF的度数;
(3)当∠COD旋转至如图3所示位置,作∠EOF的角平分线ON,求∠EON的度数。
要点6
有关钟表的角度问题
例6:在0时到12时之间,钟面上的时针与分针在什么时候成60
的角?试着尽可能多地找出答案.秒针与时针又共有多少次成的角?
变式1:钟表上12点15分时,时针和分针的夹角是
。
变式2:有一只手表每小时比准确时间慢3分钟,若在清晨4:30与准确时间对准,则当天上午手表指示的时间是10:50,准确时间应该是
。
变式3:某人下午6点多外出购物,表上的时针和分针的夹角恰为110°,下午近7点回家,发现表上的时针和分针的夹角又是110°,试算一算此人外出共用了多长时间?
变式4:时针在下午4点至5点的什么时刻:①分针和时针重合?②分针和时针成一条直线?③分针和时针成角?
巩
固
练
习
一、单选题
1.用两块角度分别为30°、60°、90°和45°、45°、90°的三角板画角,不可能画出的角是(
)
A.
125°
B.
105°
C.
75°
D.
15°
2.如图∠BCA=90,CD⊥AB,则图中互余的角有(
)对.
A.
1
B.
2
C.
3
D.
4
3.如图,一副三角尺按不同的位置摆放,摆放位置中的图形有
A.
1个
B.
2个
C.
3个
D.
4个
4.如右图所示正方形格中,连接,观测=(
)
A
.120°
B.
125°
C.130°
D.
135°
5.下列说法正确的是( )
A.
角的边越长,角度就越大
B.
周角就是一条射线
C.
一条直线可以看成平角
D.
平角的两边可以构成一条直线
6.将一副常规的三角尺按如图方式放置,则图中∠AOB的度数为(
)
A.
75?
B.
105?
C.
95?
D.
120?
7、如图,∠AOB是直角,OA平分∠COD,OE平分∠BOD,若∠BOE=23°,则∠BOC的度数是( )
A.113°
B.134°
C.136°
D.144°
8.一副三角板按如图所示的方式摆放,且∠1比∠2大50°,则∠2的度数为( )
A.
20°
B.
50°
C.
70°
D.
30°
9.∠AOB=45°,∠BOC=75°,OD平分∠AOB,OE平分∠BOC,则∠DOE=( )
A.
60°
B.
75°
C.
60°或15°
D.
70°或15°
10.已知:岛P位于岛Q的正西方,由岛P、Q分别测得船R位于南偏东30°和南偏西45°方向上,则符合条件的示意图是(
)
ABC.
D.
二、填空题
11.60.56°=______度_____分_____秒,28°28′12"=_________°;
12.一个锐角的余角是38°28′5′′,则这个角的补角是________.
13.八时三十分,时针与分针夹角度数是_______.
14.如图,点C在直线MN上,AC⊥BC于点C,∠1=65°,则∠2=____°源:
15.如图,O为直线AB上一点,OC平分∠AOD,∠AOC=53°17′,则∠BOD的度数为_____.
16.如图所示,O是直线AB上一点,OD平分∠BOC,
∠COE=90°,若∠AOC=40°,则∠DOE=_________.[]
三、解答题
17.计算:
(1)179°-72°18'54″;
(2)360°÷7(精确到秒).
18.已知一个角的补角比这个角的余角的4倍大15°,求这个角的度数。
19.如图,已知直线AB和CD相交于点O,∠COE=
90,
OF平分∠AOE,
∠COF=28.求∠AOC的度数.
20.如图,已知∠COB=3∠AOC,OD平分∠AOB,且∠AOB=120°,求∠COD的度数.
21.如图,将一副三角尺的直角顶点叠放在点C处,∠D=30°,∠B=45°,求:
(1)若∠DCE=35°,求∠ACB的度数;(2)若∠ACB=120°,求∠DCE的度数.
(3)猜想∠ACB和∠DCE的关系,并说明理由;
22.如图,∠AOB=115°,∠EOF
=155°,OA平分∠EOC,OB平分∠DOF,
(1)求∠AOE+∠FOB度数;
(2)求∠COD度数。
[]能力提升
23.点O为直线AB上一点,过点O作射线OC,使∠BOC=65°,将一直角三角板的直角顶点放在点O处.
[]
(1)如图1,将三角板MON的一边ON与射线OB重合时,则∠MOC=__________
(2)如图2,将三角板MON绕点O逆时针旋转一定角度,此时OC是∠MOB的平分线,求∠BON和∠CON的度数.
24.已知:如图,,.
(1)当时,=_________;[来源:学
科
网Z
X
X
K]
(2)当,时,_________;
(3)当,时,____________;
(4)猜想不论的度数是多少,的度数与的关系,并简述理由.
