人教版七年级数学上册3.1.2 等式的性质同步检测(word版含答案)
文档属性
| 名称 | 人教版七年级数学上册3.1.2 等式的性质同步检测(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 87.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-02 19:42:48 | ||
图片预览



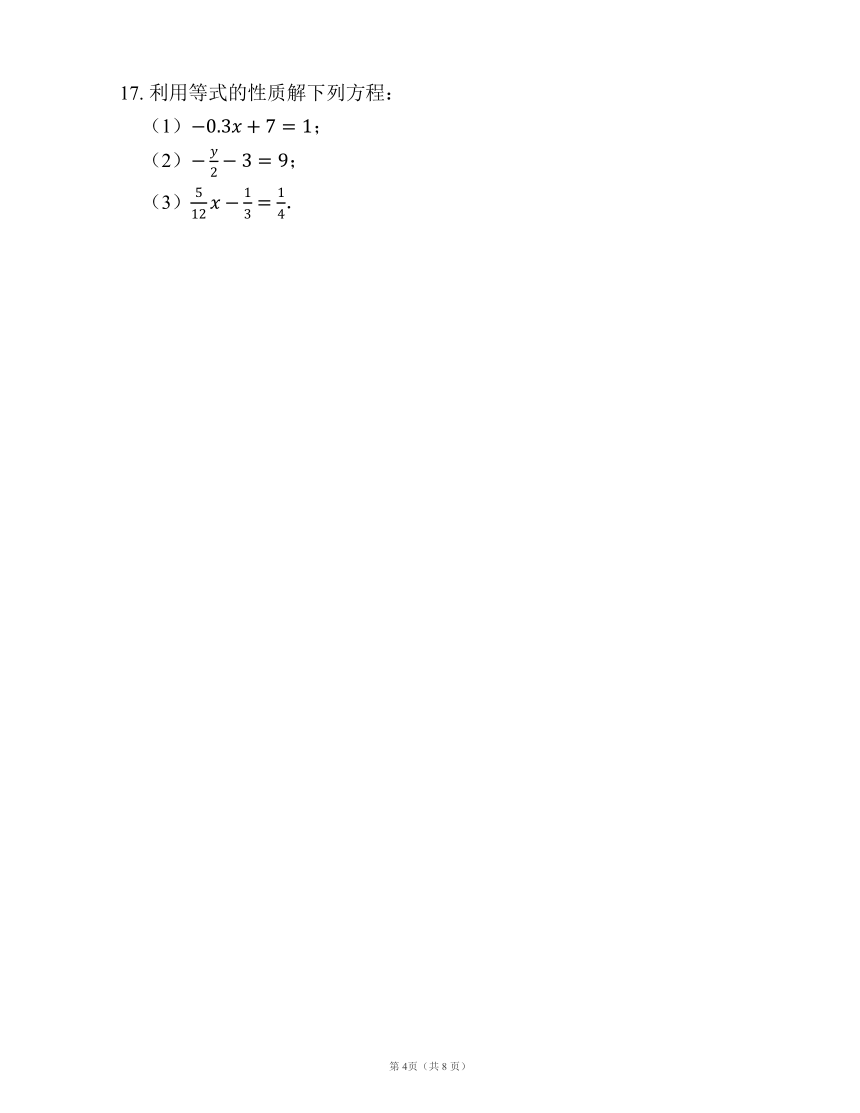
文档简介
3.1.2
等式的性质
一、选择题(共6小题;共30分)
1.
若
,且
,则下面各式中不一定正确的是
A.
B.
C.
D.
2.
已知
,根据等式性质变形为
,那么
,
必须符合的条件是
A.
B.
C.
D.
,
可以是任意有理数或整式
3.
把方程
变形为
,其依据是
A.
等式的性质
B.
等式的性质
C.
分式的基本性质
D.
不等式的性质
4.
下列结论正确的是
A.
若
,则
B.
若
,则
C.
若
,则
D.
若
,则
5.
下列是等式
的变形,其中是根据等式性质
变形的是
A.
B.
C.
D.
6.
下列说法正确的是
A.
在等式
的两边同时除以
,可得
B.
在等式
的两边同时除以
,可得
C.
在等式
的两边同时除以
,可得
D.
在等式
的两边同时加
,可得
二、填空题(共3小题;共18分)
7.
完成下列解方程:.
解:两边
?,根据
?
得
?.
于是
?.
两边
?,根据
?
得
?.
8.
如果
是关于
的一元一次方程,那么
?,此时方程的解是
?.
9.
“”“”“”分别表示三种不同的物体.如图所示,天平①②保持平衡,如果要使天平③也平衡,那么应在天平③的右端放
?
个“”.
三、解答题(共8小题;共104分)
10.
在下列各题的横线上填上适当的数或整式,使所得结果仍是等式,并说明是根据等式的哪一条性质以及是怎样变形的.
(1)如果
,那么
?
,根据
?;
(2)如果
,那么
?,根据
?;
(3)如果
,那么
?,根据
?.
11.
当
为何值时,式子
的值为
?
12.
已知方程
的解是
,试求
的值.
13.
将
的两边都除以
,得
,对其中错误的原因,四名同学归纳如下:甲说“方程本身是错误的.”乙说:“方程无解.”丙说:“方程两边不能除以
.”丁说:“
小于
.”请谈谈你的看法.
14.
已知
,你能求出
的值吗?说明过程.
15.
能不能从
得到
,为什么?反之,能不能从
得到等式
,为什么?
16.
运用等式的性质解下列方程并检验:
(1);
(2);
(3);
(4).
17.
利用等式的性质解下列方程:
(1);
(2);
(3).
答案
第一部分
1.
D
2.
C
3.
B
4.
D
5.
D
6.
B
第二部分
7.
都减去,等式的性质,,,都乘(或除以),等式的性质,
8.
,
9.
【解析】提示
,
.
第三部分
10.
(1)
;等式的性质
,两边都减去
.
??????(2)
;等式的性质
,两边都乘
.
??????(3)
;等式的性质
,两边都除以
.
11.
由题意,得
两边同时加上
,得
两边同时除以
,得
12.
因为
的解是
,
所以
,解得
.
所以
.
13.
我认为丙的说法是正确的,题中的做法不符合等式的性质.
当
时,.
14.
由
,得
所以
15.
不能从
得到
.
当
时,.
因为
不能做除数,
所以从
不能得到
.
而从
可以得到等式
,依据是等式的性质
.
16.
(1)
方程两边同时减去
,得
于是,得
检验:当
时,左边
右边.
所以
是原方程的解.
??????(2)
方程两边同时除以
,得
于是,得
检验:当
时,左边
右边.
所以
是原方程的解.
??????(3)
方程两边同时减去
,得
于是,得
检验:当
时,左边
,
右边
,
所以
左边
右边.
所以
是原方程的解.
??????(4)
方程两边同时减去
,得
于是,得
方程两边同时乘以
,得
检验:当
时,右边
,
所以
左边
右边.
所以
是原方程的解.
17.
(1)
方程两边同时减去
,得
于是,得
方程两边同时除以
,得
于是,得
??????(2)
方程两边同时加上
,得
于是,得
方程两边同时乘以
,得
??????(3)
方程两边同时乘以
,得
方程两边同时加上
,得
于是,得
方程两边同时除以
,得
第1页(共8
页)
等式的性质
一、选择题(共6小题;共30分)
1.
若
,且
,则下面各式中不一定正确的是
A.
B.
C.
D.
2.
已知
,根据等式性质变形为
,那么
,
必须符合的条件是
A.
B.
C.
D.
,
可以是任意有理数或整式
3.
把方程
变形为
,其依据是
A.
等式的性质
B.
等式的性质
C.
分式的基本性质
D.
不等式的性质
4.
下列结论正确的是
A.
若
,则
B.
若
,则
C.
若
,则
D.
若
,则
5.
下列是等式
的变形,其中是根据等式性质
变形的是
A.
B.
C.
D.
6.
下列说法正确的是
A.
在等式
的两边同时除以
,可得
B.
在等式
的两边同时除以
,可得
C.
在等式
的两边同时除以
,可得
D.
在等式
的两边同时加
,可得
二、填空题(共3小题;共18分)
7.
完成下列解方程:.
解:两边
?,根据
?
得
?.
于是
?.
两边
?,根据
?
得
?.
8.
如果
是关于
的一元一次方程,那么
?,此时方程的解是
?.
9.
“”“”“”分别表示三种不同的物体.如图所示,天平①②保持平衡,如果要使天平③也平衡,那么应在天平③的右端放
?
个“”.
三、解答题(共8小题;共104分)
10.
在下列各题的横线上填上适当的数或整式,使所得结果仍是等式,并说明是根据等式的哪一条性质以及是怎样变形的.
(1)如果
,那么
?
,根据
?;
(2)如果
,那么
?,根据
?;
(3)如果
,那么
?,根据
?.
11.
当
为何值时,式子
的值为
?
12.
已知方程
的解是
,试求
的值.
13.
将
的两边都除以
,得
,对其中错误的原因,四名同学归纳如下:甲说“方程本身是错误的.”乙说:“方程无解.”丙说:“方程两边不能除以
.”丁说:“
小于
.”请谈谈你的看法.
14.
已知
,你能求出
的值吗?说明过程.
15.
能不能从
得到
,为什么?反之,能不能从
得到等式
,为什么?
16.
运用等式的性质解下列方程并检验:
(1);
(2);
(3);
(4).
17.
利用等式的性质解下列方程:
(1);
(2);
(3).
答案
第一部分
1.
D
2.
C
3.
B
4.
D
5.
D
6.
B
第二部分
7.
都减去,等式的性质,,,都乘(或除以),等式的性质,
8.
,
9.
【解析】提示
,
.
第三部分
10.
(1)
;等式的性质
,两边都减去
.
??????(2)
;等式的性质
,两边都乘
.
??????(3)
;等式的性质
,两边都除以
.
11.
由题意,得
两边同时加上
,得
两边同时除以
,得
12.
因为
的解是
,
所以
,解得
.
所以
.
13.
我认为丙的说法是正确的,题中的做法不符合等式的性质.
当
时,.
14.
由
,得
所以
15.
不能从
得到
.
当
时,.
因为
不能做除数,
所以从
不能得到
.
而从
可以得到等式
,依据是等式的性质
.
16.
(1)
方程两边同时减去
,得
于是,得
检验:当
时,左边
右边.
所以
是原方程的解.
??????(2)
方程两边同时除以
,得
于是,得
检验:当
时,左边
右边.
所以
是原方程的解.
??????(3)
方程两边同时减去
,得
于是,得
检验:当
时,左边
,
右边
,
所以
左边
右边.
所以
是原方程的解.
??????(4)
方程两边同时减去
,得
于是,得
方程两边同时乘以
,得
检验:当
时,右边
,
所以
左边
右边.
所以
是原方程的解.
17.
(1)
方程两边同时减去
,得
于是,得
方程两边同时除以
,得
于是,得
??????(2)
方程两边同时加上
,得
于是,得
方程两边同时乘以
,得
??????(3)
方程两边同时乘以
,得
方程两边同时加上
,得
于是,得
方程两边同时除以
,得
第1页(共8
页)
