沪科版(2012)初中数学七年级下册 10.2.2 平行线的判定 教案
文档属性
| 名称 | 沪科版(2012)初中数学七年级下册 10.2.2 平行线的判定 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 69.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-03 00:00:00 | ||
图片预览



文档简介
《10.2平行线的判定3》教学设计
教学目标:
1、掌握三种平行线的判定方法,并会用所学的方法来判断两条直线是否平行。
2、会利用同位角相等判断两直线平行的方法来推导出另外两种判定方法(内错角、同旁内角)。
3、会根据平行线的判定方法进行简单的推理并学会用数学符号写出简单的推理过程。
4、体会数学中的转化思想。
教学重难点:
1、教学重点:对平行线判定方法的概括与推导。
2、教学难点:平行线判定方法的归纳与综合运用。
教学过程:
一、复习导入。
思考:两条直线被第三条直线所截,同时得到同位角、内错角和同旁内角,由同位角相等可以判定两直线平行,那么,能否利用内错角和同旁内角来判定两直线平行呢?
二、新授。
(一)探究1:如果
∠2
=
∠3,能否推出
a//b呢?
解:
∵
∠2
=
∠3
(已知)
∠
1=
∠
3
(对顶角相等)
∴
∠1=
∠2
(等量代换)
∴
a∥b
(同位角相等,两直线平行)
得出结论:平行线的判定方法2:两条直线被第三条直线所截,如果
内错角相等,那么这两条直线平行。
简单说成:内错角相等,两直线平行。
几何语言描述:∵
∠
1=
∠2
∴
a∥b
(内错角相等,两直线平行)
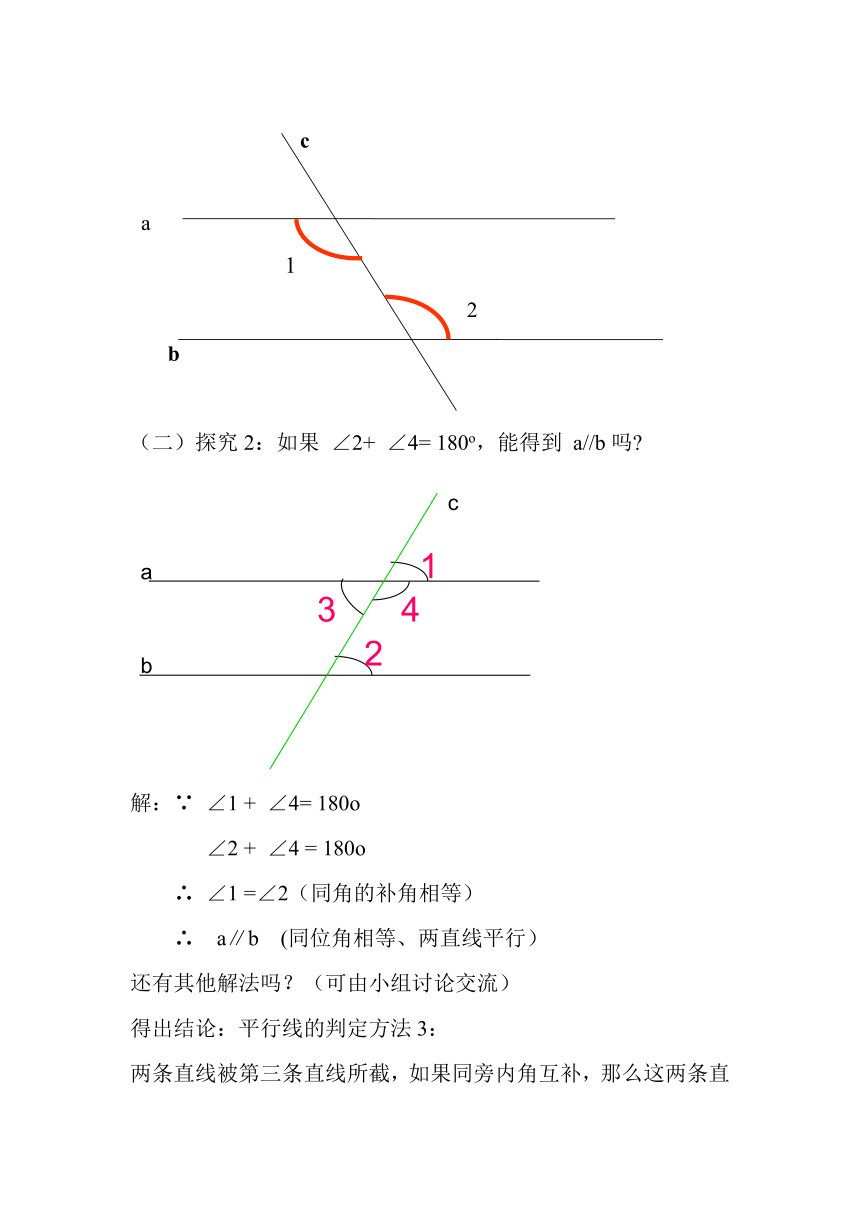
(二)探究2:如果
∠2+
∠4=
180o,能得到
a//b吗?
解:∵
∠1
+
∠4=
180o
∠2
+
∠4
=
180o
∴
∠1
=∠2(同角的补角相等)
∴
a∥b
(同位角相等、两直线平行)
还有其他解法吗?(可由小组讨论交流)
得出结论:平行线的判定方法3:
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行。
简单说成:同旁内角互补,两直线平行。
几何语言描述:
∵
∠1+∠2=180o
∴
a∥b
(同旁内角互补,两直线平行)
(三)例题讲解
已知∠3=45
°,∠1与∠2互余,你能得到AB//CD吗?
解:∵∠1与∠2互余(已知),
∠1=∠2(对顶角相等)
∴∠1=∠2=45°
∵
∠3=45°
∴∠
2=∠3
∴
AB∥CD(内错角相等,两直线平行)
三、试一试。
(1)∵∠1=∠B(已知)
∴__∥__
(
)
(2)∵∠1=∠D(已知)
∴
∥
(
)
(3)∵∠B+∠BAD=180°(已知)
∴
∥
(
)
(4)∵∠_
=
∠_(已知)
∴AB∥CD
(
)
四、巩固提高。
1、如果∠A
+∠B
=180°,那么根据同旁内
角互补,两直线平行,可得_____∥_____;
如果
+∠B
=180°,那么根据同旁内角
互补,两直线平行,可得AB∥EC。
3、如图,∠
C=61
。
当∠ABE=
度时,EF∥CN
当∠CBF=
度时,EF∥CN
五、小结。
平行线的判定示意图
同位角相等
内错角相等
两直线平行
同旁内角互补
位置关系
数量关系
六、作业。
七、板书设计。
平行线的判定示意图
同位角相等
内错角相等
两直线平行
同旁内角互补
位置关系
数量关系
a
b
c
1
2
3
a
b
c
1
2
a
b
c
1
2
3
4
a
b
c
2
1
1
2
3
A
B
C
D
2、直线a、b与直线c相交,给出下列条件:
①∠1=
∠2②∠3=
∠6③∠4+∠7=1800
④∠3+
∠5=1800,其中能判断a//b的是
(
)
A
①②③④
B
①③④
C
①③
D
④
A
B
C
E
6
4
1
5
7
3
2
8
a
b
A
B
C
N
E
F
教学目标:
1、掌握三种平行线的判定方法,并会用所学的方法来判断两条直线是否平行。
2、会利用同位角相等判断两直线平行的方法来推导出另外两种判定方法(内错角、同旁内角)。
3、会根据平行线的判定方法进行简单的推理并学会用数学符号写出简单的推理过程。
4、体会数学中的转化思想。
教学重难点:
1、教学重点:对平行线判定方法的概括与推导。
2、教学难点:平行线判定方法的归纳与综合运用。
教学过程:
一、复习导入。
思考:两条直线被第三条直线所截,同时得到同位角、内错角和同旁内角,由同位角相等可以判定两直线平行,那么,能否利用内错角和同旁内角来判定两直线平行呢?
二、新授。
(一)探究1:如果
∠2
=
∠3,能否推出
a//b呢?
解:
∵
∠2
=
∠3
(已知)
∠
1=
∠
3
(对顶角相等)
∴
∠1=
∠2
(等量代换)
∴
a∥b
(同位角相等,两直线平行)
得出结论:平行线的判定方法2:两条直线被第三条直线所截,如果
内错角相等,那么这两条直线平行。
简单说成:内错角相等,两直线平行。
几何语言描述:∵
∠
1=
∠2
∴
a∥b
(内错角相等,两直线平行)
(二)探究2:如果
∠2+
∠4=
180o,能得到
a//b吗?
解:∵
∠1
+
∠4=
180o
∠2
+
∠4
=
180o
∴
∠1
=∠2(同角的补角相等)
∴
a∥b
(同位角相等、两直线平行)
还有其他解法吗?(可由小组讨论交流)
得出结论:平行线的判定方法3:
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行。
简单说成:同旁内角互补,两直线平行。
几何语言描述:
∵
∠1+∠2=180o
∴
a∥b
(同旁内角互补,两直线平行)
(三)例题讲解
已知∠3=45
°,∠1与∠2互余,你能得到AB//CD吗?
解:∵∠1与∠2互余(已知),
∠1=∠2(对顶角相等)
∴∠1=∠2=45°
∵
∠3=45°
∴∠
2=∠3
∴
AB∥CD(内错角相等,两直线平行)
三、试一试。
(1)∵∠1=∠B(已知)
∴__∥__
(
)
(2)∵∠1=∠D(已知)
∴
∥
(
)
(3)∵∠B+∠BAD=180°(已知)
∴
∥
(
)
(4)∵∠_
=
∠_(已知)
∴AB∥CD
(
)
四、巩固提高。
1、如果∠A
+∠B
=180°,那么根据同旁内
角互补,两直线平行,可得_____∥_____;
如果
+∠B
=180°,那么根据同旁内角
互补,两直线平行,可得AB∥EC。
3、如图,∠
C=61
。
当∠ABE=
度时,EF∥CN
当∠CBF=
度时,EF∥CN
五、小结。
平行线的判定示意图
同位角相等
内错角相等
两直线平行
同旁内角互补
位置关系
数量关系
六、作业。
七、板书设计。
平行线的判定示意图
同位角相等
内错角相等
两直线平行
同旁内角互补
位置关系
数量关系
a
b
c
1
2
3
a
b
c
1
2
a
b
c
1
2
3
4
a
b
c
2
1
1
2
3
A
B
C
D
2、直线a、b与直线c相交,给出下列条件:
①∠1=
∠2②∠3=
∠6③∠4+∠7=1800
④∠3+
∠5=1800,其中能判断a//b的是
(
)
A
①②③④
B
①③④
C
①③
D
④
A
B
C
E
6
4
1
5
7
3
2
8
a
b
A
B
C
N
E
F
