第6章平面图形的认识(一) 单元复习二(提升卷)-苏科版七年级数学上册期末复习(word版含答案)
文档属性
| 名称 | 第6章平面图形的认识(一) 单元复习二(提升卷)-苏科版七年级数学上册期末复习(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 184.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-03 09:00:47 | ||
图片预览


文档简介
第六章《平面图形的认识(一)》单元复习二(提优卷)
一、选择题
1.给出下列说法:①过两点有且只有一条直线;②连接两点的线段叫作两点间的距离;③两点之间,线段最短;④若AB=BC,则点B是线段AC的中点;⑤射线AB和射线BA是同一条射线;⑥直线有无数个端点.其中正确的个数是 ( )
A.2 B.3 C.4 D.5
2.面上有三点,经过每两点作一条直线,则能作出的直线的条数是 ( )
A.1条 B.3条 C.1条或3条 D.以上都不对
3.在下面各图中,么1与么2是对顶角是 ( )
4.如图,两条直线AB,CD交于点O,射线OM是∠AOC的平分线,若∠BOD=80°,则∠BOM等于 ( )
A.40° B.120° C.140° D.100°
5.如图,C岛在A岛的北偏东50°方向,C岛在B岛的北偏西40°方向,则从C岛看A,B两岛的视角∠ACB等于 ( )
A.90° B.80° C.70° D.60°
6.如图,把水渠中的水引到水池C,先过C点向渠岸AB画垂线,垂足为点D,再沿垂线CD开沟才能使沟最短,其依据是 ( )
A.垂线最短 B.过一点确定一条直线与已知直线垂直
C.垂线段最短 D.以上说法都不对
7.观察图形,下列说法正确的个数有 ( )
(1)直线BA和直线AB是同一条直线;
(2)射线AC和射线AD是同一条射线;
(3)AB+BD>AD;
(4)三条直线两两相交时,一定有三个交点.
A.1个 B.2个 C.3个 D.4个
8.若∠1和∠2互余,∠1与∠3互补,∠2与∠3的和等于周角的,则∠1、∠2、∠3这三个角分别是 ( )
A.50°,30°,130° B.70°,20°,110°
C.75°,15°,105° D.60°,30°,120°
9.如图,∠1=15°,∠AOC=90°,点B、O、D在同一直线上,则∠2的度数为 ( )
A.75°
B.15°
C.105°
D.165°
10.下列说法正确的个数是 ( )
①过直线上或直线外一点,能且只能画这条直线的一条垂线;②过直线l上一点A和直线l外一点B,都能画这条直线l的垂线;③从直线外一点作这条直线的垂线段,叫做这个点到这条直线的距离;④过直线外一点画这条直线的垂线,垂线的长度叫做这点到这条直线的距离.
A.1个 B.2个 C.3个 D.4个
二、填空题(每小题3分,共24分)
11.已知线段AB=10 cm,BC=5 cm,A、B、C三点在同一条直线上,则
AC=_ _.
12.已知线段AB=1 996 cm,P、Q是线段AB上的两个点,线段AQ=
1 200 cm,线段BP=1 050 cm,则线段PQ=___________.
13.如图,OM平分∠AOB,ON平分∠COD.若∠MON=50°,∠BOC=10°,则∠AOD= __________.
14.如图,线段AB=BC=CD=DE=1 cm,那么图中所有线段的长度之和等于________cm.
15.一条直线上距离相等的立有10根标杆,一名学生匀速地从第1根标杆向第10根标杆行走,当他走到第6根标杆时用了6.5 s,则当他走到第10根标杆时所用时间是_________.
16.平面内三条直线两两相交,最多有a个交点,最少有b个交点,则a+b=___________.
17.上午九点时分针与时针互相垂直,再经过 分钟后分针与时针第一次成一条直线.
18. 如图,点O是直线AD上一点,射线OC、OE分别是∠AOB、∠BOD的平分线,若∠AOC=28°,则∠COD=_________,∠BOE=__________.
19.已知∠AOB=50°,∠AOC=110°,分别作∠AOB和∠AOC的平分线OM、ON,∠MON=_____.
20.从4点15分到4点40分,时钟的时针转了_______°,分针转了_______°;4点40分时,时针和分针的夹角是_______°.
三、解答题
21.如图,已知B,C是线段AD上的两点,且AB:BC:CD=2:4:3,M是AD的中点,CD=6 cm,求线段MC的长.
22. 已知∠α与∠β互为补角,且∠α比∠β大42°,求这两个角.
23. 已知线段AB=10 cm,试探讨下列问题:
(1) 是否存在一点C,使它到A,B两点的距离之和等于8 cm?
(2) 是否存在一点C,使它到A,B两点的距离之和等手10 cm? 若存在,它的位置唯一吗?
(3) 当点C到A,B两点的距离之和等于20 cm时,点C一定在直线AB外吗? 举例说明.
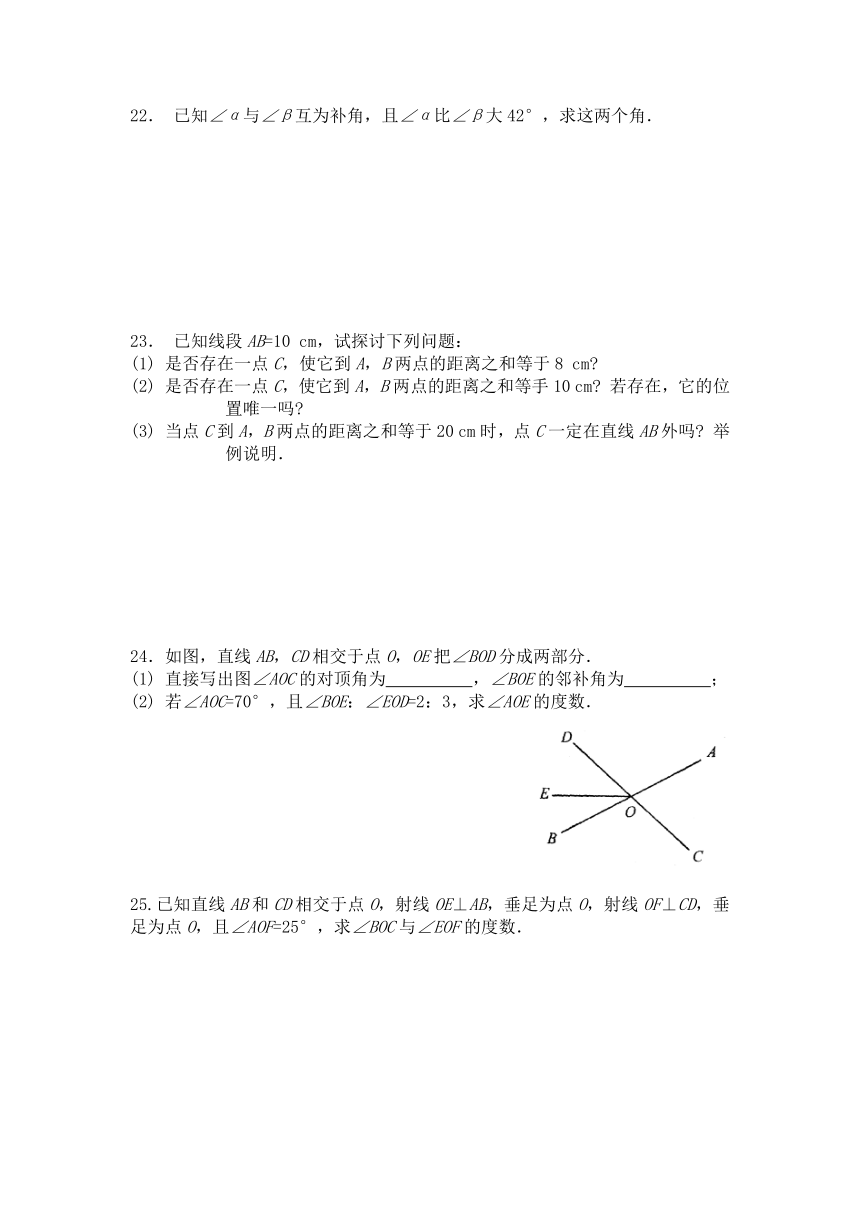
24.如图,直线AB,CD相交于点O,OE把∠BOD分成两部分.
(1) 直接写出图∠AOC的对顶角为 ,∠BOE的邻补角为 ;
(2) 若∠AOC=70°,且∠BOE:∠EOD=2:3,求∠AOE的度数.
25.已知直线AB和CD相交于点O,射线OE⊥AB,垂足为点O,射线OF⊥CD,垂足为点O,且∠AOF=25°,求∠BOC与∠EOF的度数.
26.如图,点D在∠BAC的内部,请根据下列要求画图,并回答问题:
(1) 过点D画直线DE∥AB,交AC于点E;
(2) 过点D画直线DF∥AC,交AB于点F;
(3) 通过测量判断AE与DF的大小关系以及∠A与∠EDF的大小关系.
27.已知∠AOB是一个直角,作射线OC,再分别作∠AOC和∠BOC的平分线OD,OE.
(1) 如图1,当∠BOC=70°时,求∠DOE的度数.
(2) 如图2,当射线OC在∠AOB内绕点O旋转时,∠DOE的大小是否发生变化?说明理由.
(3) 当射线OC在∠AOB外绕点O旋转且∠AOC为钝角时,画出图形,直接写出相应的∠DOE的度数.(不必写出过程)
第六章《平面图形的认识(一)》单元复习二(提优卷)
参考答案
一、选择题
1.A 2.C 3.B 4.C 5.A 6.C 7.C 8.C 9.C 10.B
二、填空题
11.5 cm或15 cm 12. 254 cm 13. 90° 14.20 15.11.7 s 16.4 17.
18.152° 62° 19.30°或80° 20.12.5 150 100
三、解答题
21.由AB:BC:CD=2:4:3,设AB=2x cm,BC=4x cm,CD=3x cm,则CD=3x=6,解得x=2.因此,AD=AB+BC+CD=2x+4x+3x=18 (cm).因为点M是AD的中点,所以DM=AD=×18=9 (cm),MC=DM-CD=9-6=3(cm)
22.设∠α的度数为x,则∠β的度数为180°-x,因此,有x-(180°-x)=42°,解得x=111°,则180°-x=69°,即∠α的度数为111°,∠β的度数为69°
23.(1) 不存在 (2) 存在,位置不唯一 (3) 不一定,也可在直线AB上,如图,线段AB=10 cm,AC=5 cm
24.(1) ∠BOD ∠AOE (2) 因为∠DOB=∠AOC=70°,∠DOB=∠BOE+∠EOD,因为∠BOE:∠EOD=2:3,所以得∠EOD=∠BOE,所以∠BOE+∠BOE=70°,所以∠BOE=28°,所以∠AOE=180°-∠BOE=152°
25.因为OF⊥CD,所以∠FOD=90°,所以∠AOD=∠AOF+∠FOD=25°+90°=115°,所以∠BOC=115°.因为OE⊥AB,所以∠AOE=90°,所以∠EOF=90°-25°=65°
26.(1)、(2) 图略 (3) AE=DF ∠A=∠EDF
27.(1) 根据题意得∠AOC=90°-∠BOC=20°.因为OD,OE分别平分∠AOC和∠BOC,所以∠COD=∠AOC=10°,∠COE=∠BOC=35°,所以∠DOE=∠COD+∠COE=45° (2) ∠DOE的大小不变,理由:∠DOE=∠COD+∠COE=∠AOC+∠COB=(∠AOC+∠COB)=∠AOB=45° (3) ∠DOE的大小发生变化.如图3,则∠DOE为45°;如图4,则∠DOE为135°
一、选择题
1.给出下列说法:①过两点有且只有一条直线;②连接两点的线段叫作两点间的距离;③两点之间,线段最短;④若AB=BC,则点B是线段AC的中点;⑤射线AB和射线BA是同一条射线;⑥直线有无数个端点.其中正确的个数是 ( )
A.2 B.3 C.4 D.5
2.面上有三点,经过每两点作一条直线,则能作出的直线的条数是 ( )
A.1条 B.3条 C.1条或3条 D.以上都不对
3.在下面各图中,么1与么2是对顶角是 ( )
4.如图,两条直线AB,CD交于点O,射线OM是∠AOC的平分线,若∠BOD=80°,则∠BOM等于 ( )
A.40° B.120° C.140° D.100°
5.如图,C岛在A岛的北偏东50°方向,C岛在B岛的北偏西40°方向,则从C岛看A,B两岛的视角∠ACB等于 ( )
A.90° B.80° C.70° D.60°
6.如图,把水渠中的水引到水池C,先过C点向渠岸AB画垂线,垂足为点D,再沿垂线CD开沟才能使沟最短,其依据是 ( )
A.垂线最短 B.过一点确定一条直线与已知直线垂直
C.垂线段最短 D.以上说法都不对
7.观察图形,下列说法正确的个数有 ( )
(1)直线BA和直线AB是同一条直线;
(2)射线AC和射线AD是同一条射线;
(3)AB+BD>AD;
(4)三条直线两两相交时,一定有三个交点.
A.1个 B.2个 C.3个 D.4个
8.若∠1和∠2互余,∠1与∠3互补,∠2与∠3的和等于周角的,则∠1、∠2、∠3这三个角分别是 ( )
A.50°,30°,130° B.70°,20°,110°
C.75°,15°,105° D.60°,30°,120°
9.如图,∠1=15°,∠AOC=90°,点B、O、D在同一直线上,则∠2的度数为 ( )
A.75°
B.15°
C.105°
D.165°
10.下列说法正确的个数是 ( )
①过直线上或直线外一点,能且只能画这条直线的一条垂线;②过直线l上一点A和直线l外一点B,都能画这条直线l的垂线;③从直线外一点作这条直线的垂线段,叫做这个点到这条直线的距离;④过直线外一点画这条直线的垂线,垂线的长度叫做这点到这条直线的距离.
A.1个 B.2个 C.3个 D.4个
二、填空题(每小题3分,共24分)
11.已知线段AB=10 cm,BC=5 cm,A、B、C三点在同一条直线上,则
AC=_ _.
12.已知线段AB=1 996 cm,P、Q是线段AB上的两个点,线段AQ=
1 200 cm,线段BP=1 050 cm,则线段PQ=___________.
13.如图,OM平分∠AOB,ON平分∠COD.若∠MON=50°,∠BOC=10°,则∠AOD= __________.
14.如图,线段AB=BC=CD=DE=1 cm,那么图中所有线段的长度之和等于________cm.
15.一条直线上距离相等的立有10根标杆,一名学生匀速地从第1根标杆向第10根标杆行走,当他走到第6根标杆时用了6.5 s,则当他走到第10根标杆时所用时间是_________.
16.平面内三条直线两两相交,最多有a个交点,最少有b个交点,则a+b=___________.
17.上午九点时分针与时针互相垂直,再经过 分钟后分针与时针第一次成一条直线.
18. 如图,点O是直线AD上一点,射线OC、OE分别是∠AOB、∠BOD的平分线,若∠AOC=28°,则∠COD=_________,∠BOE=__________.
19.已知∠AOB=50°,∠AOC=110°,分别作∠AOB和∠AOC的平分线OM、ON,∠MON=_____.
20.从4点15分到4点40分,时钟的时针转了_______°,分针转了_______°;4点40分时,时针和分针的夹角是_______°.
三、解答题
21.如图,已知B,C是线段AD上的两点,且AB:BC:CD=2:4:3,M是AD的中点,CD=6 cm,求线段MC的长.
22. 已知∠α与∠β互为补角,且∠α比∠β大42°,求这两个角.
23. 已知线段AB=10 cm,试探讨下列问题:
(1) 是否存在一点C,使它到A,B两点的距离之和等于8 cm?
(2) 是否存在一点C,使它到A,B两点的距离之和等手10 cm? 若存在,它的位置唯一吗?
(3) 当点C到A,B两点的距离之和等于20 cm时,点C一定在直线AB外吗? 举例说明.
24.如图,直线AB,CD相交于点O,OE把∠BOD分成两部分.
(1) 直接写出图∠AOC的对顶角为 ,∠BOE的邻补角为 ;
(2) 若∠AOC=70°,且∠BOE:∠EOD=2:3,求∠AOE的度数.
25.已知直线AB和CD相交于点O,射线OE⊥AB,垂足为点O,射线OF⊥CD,垂足为点O,且∠AOF=25°,求∠BOC与∠EOF的度数.
26.如图,点D在∠BAC的内部,请根据下列要求画图,并回答问题:
(1) 过点D画直线DE∥AB,交AC于点E;
(2) 过点D画直线DF∥AC,交AB于点F;
(3) 通过测量判断AE与DF的大小关系以及∠A与∠EDF的大小关系.
27.已知∠AOB是一个直角,作射线OC,再分别作∠AOC和∠BOC的平分线OD,OE.
(1) 如图1,当∠BOC=70°时,求∠DOE的度数.
(2) 如图2,当射线OC在∠AOB内绕点O旋转时,∠DOE的大小是否发生变化?说明理由.
(3) 当射线OC在∠AOB外绕点O旋转且∠AOC为钝角时,画出图形,直接写出相应的∠DOE的度数.(不必写出过程)
第六章《平面图形的认识(一)》单元复习二(提优卷)
参考答案
一、选择题
1.A 2.C 3.B 4.C 5.A 6.C 7.C 8.C 9.C 10.B
二、填空题
11.5 cm或15 cm 12. 254 cm 13. 90° 14.20 15.11.7 s 16.4 17.
18.152° 62° 19.30°或80° 20.12.5 150 100
三、解答题
21.由AB:BC:CD=2:4:3,设AB=2x cm,BC=4x cm,CD=3x cm,则CD=3x=6,解得x=2.因此,AD=AB+BC+CD=2x+4x+3x=18 (cm).因为点M是AD的中点,所以DM=AD=×18=9 (cm),MC=DM-CD=9-6=3(cm)
22.设∠α的度数为x,则∠β的度数为180°-x,因此,有x-(180°-x)=42°,解得x=111°,则180°-x=69°,即∠α的度数为111°,∠β的度数为69°
23.(1) 不存在 (2) 存在,位置不唯一 (3) 不一定,也可在直线AB上,如图,线段AB=10 cm,AC=5 cm
24.(1) ∠BOD ∠AOE (2) 因为∠DOB=∠AOC=70°,∠DOB=∠BOE+∠EOD,因为∠BOE:∠EOD=2:3,所以得∠EOD=∠BOE,所以∠BOE+∠BOE=70°,所以∠BOE=28°,所以∠AOE=180°-∠BOE=152°
25.因为OF⊥CD,所以∠FOD=90°,所以∠AOD=∠AOF+∠FOD=25°+90°=115°,所以∠BOC=115°.因为OE⊥AB,所以∠AOE=90°,所以∠EOF=90°-25°=65°
26.(1)、(2) 图略 (3) AE=DF ∠A=∠EDF
27.(1) 根据题意得∠AOC=90°-∠BOC=20°.因为OD,OE分别平分∠AOC和∠BOC,所以∠COD=∠AOC=10°,∠COE=∠BOC=35°,所以∠DOE=∠COD+∠COE=45° (2) ∠DOE的大小不变,理由:∠DOE=∠COD+∠COE=∠AOC+∠COB=(∠AOC+∠COB)=∠AOB=45° (3) ∠DOE的大小发生变化.如图3,则∠DOE为45°;如图4,则∠DOE为135°
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
