第2章有理数 单元复习二(提优卷)-苏科版七年级数学上册期末复习(word版含答案)
文档属性
| 名称 | 第2章有理数 单元复习二(提优卷)-苏科版七年级数学上册期末复习(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 339.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-03 09:18:30 | ||
图片预览



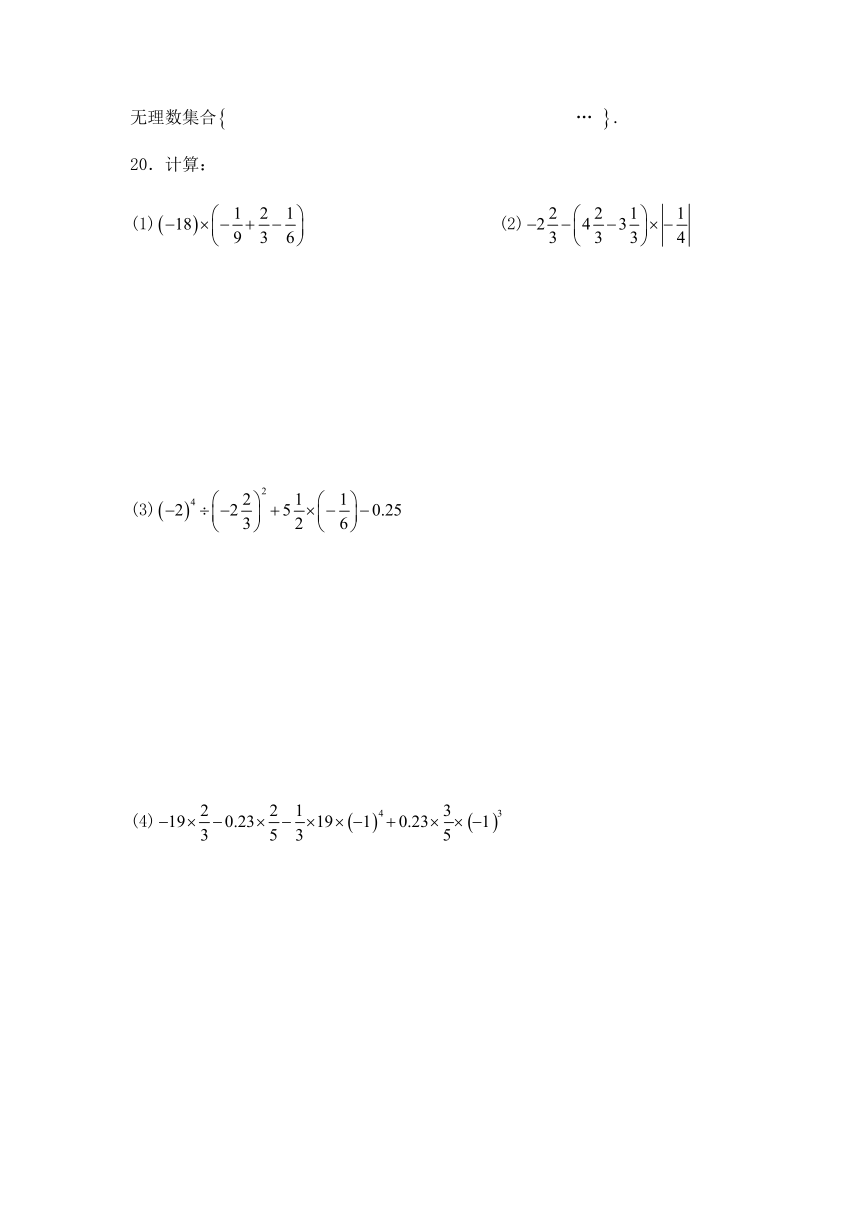
文档简介
第二章《有理数》单元复习二(提优卷)
选择题
的相反数是 ( )
A. B. C. D.
下列说法正确的个数是 ( )
①一个有理数不是整数就是分数;②无限循环小数是无理数;
③一个整数不是正的,就是负的;④一个分数不是正的,就是负的.
A.1 B.2 C. 3 D. 4
下列等式成立的是 ( )
A. B. C. D.
4.(-5)6表示的意义是 ( )
A.-5乘以6的积 B.6个-5相乘的积
C.5个-6相乘的积 D.6个-5相加的和
5.下面说法:①-a一定是负数;②若|a|=|b|,则a=b;③一个有理数中不是整数就是分数;④一个有理数不是正数就是负数.其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
6.北京故宫的面积约为720 000 m2,用科学记数法表示为 ( )
A.0.72×106m2 B.7.2×106m2 C.0.72×105m2 D.7.2×105m2
7.观察下列等式,7 1=7,7 2=49,7 3=343,。74=2 401,…,由此可以判断7100的个位数字是 ( )
A.1 B.7 C.9 D.3
8.若规定“!”是一种数学运算符号,且则的值为 ( )
A. B.99! C.9 900 D.2!
9.数学家发明了一个魔术盒,当任意有理数对进入其中时,会得到一个新的有理数:+ b -.例如,把放入其中,就会得到.现将有理数对放入其中,得到有理数,再将有理数对放入其中后,得到的有理数是 ( )
A.3 B.6 C.9 D.12
10.小王用计算机设计一个程序,输入和输出的数据如下表:
输入 ··· 1 2 3 4 5 6 ···
输出 ···
···
那么输入8时,输出的数据是 ( )
A. B. C. D.
二、填空题
11.若规定,则的值为 .
12.已知|a|=1,|b|=2,|c|=3,且a>b>c,那么a+b﹣c=________.?
13.观察下面一列数:-1,2,-3,4,-5,6,-7,…,将这列数排成图2的形式,按照上述规律排下去,那么第10行从左边数第9个数是________.
某次数学测验共20道选择题,规则是:选对一道得5分,选错一道得-1分,不选得零分,王明同学的卷面成绩是:选对16道题,选错2道题,有2道题未做,他的得分是 .
15.若数轴上的点A所表示的有理数是-2,则与点A相距5个单位长度的点所表示的有理数是____________.
16.若|a﹣1|=4,则a=________.
17.股民李金上星期六买进某公司的股票,每股27元,下表为本周内该股票涨跌情况(单位:元)
星期 一 二 三 四 五 六
每股涨跌 (与前一天相比) -1.5 -1 +6.5 +3.5 +1 -4
星期三收盘时.每股是 元;本周内最高价是每股 元;最低价是每股 元.
18. 已知|a-3|+=0,则= .
三、解答题
19. 将下列各数填入相应的括号里:
,,,8,,,,,…,,.
正数集合 …;
负数集合 …;
整数集合 …;
有理数集合 …;
无理数集合 ….
20.计算:
(1) (2)
(3)
(4)
(5)
21.阅读材料:对于任何实数,我们规定符号的意义是=ad-bc.
例如:=1×4-2×3=-2,=(-2)×5-4×3=-22.
(1)按照这个规定请你计算的值;
(2)按照这个规定请你计算:当|x-2|=0时,的值.
22.小明在复习归纳时发现初中阶段学习了三个非负数,分别是:①a2;②a;③|a|(a是任意实数).于是他结合所学习的三个非负数的知识,自己编了一道题:已知(x+2)2+|x+y﹣1|=0,求xy的值.请你利用三个非负数的知识解答这个问题
23.某自行车厂7天计划生产1400辆自行车,平均每天生产200辆,由于各种原因,无法按计划生产,下表是这7天的生产情况(超产为正,减产为负,单位:辆):
第1天 第2天 第3天 第4天 第5天 第6天 第7天
+5 -2 -6 +15 -9 -13 +8
(1)根据记录可知前4天共生产自行车______辆;
(2)自行车产量最多的一天比产量最少的一天多生产________辆;
(3)该厂实行日计件工资制,每生产一辆自行车,厂方付给工人工资60元,超额完成计划任务的,每超产一辆奖励15元,没有完成计划任务的,每减产一辆扣15元,则该厂工人这7天的工资总额是多少?
24.将图①中的正方形剪开得到图②,图②中共有个正方形;将图②中一个正方形剪开得到图③,图③中共有个正方形;将图③中一个正方形剪开得到图④;;如此下去.
()按图示规律填写下表:
图 ① ② ③ ④ ⑤
正方形个数
()按照这种方式剪下去,求第个图中有多少个正方形.
()按照这种方式剪下去,求第个图中有多少个正方形.
()按照这种方式剪下去,求第几个图中有个正方形.
25若点A、B在数轴上分别表示实数a、b,则我们可以定义|a-b|为A、B两点之间的距离,表示为|AB|=|a-b|.根据这个定义回答下列问题:
(1)数轴上表示2和5的两点之间的距离是______ ,表示-2和-5的两点之间的距离是______ ;表示1和-3的两点之间的距离是______ ;表示x和-1的两点A和B之间的距离是_____ ;
(2)如果|x+3|=2,求的值;
(3)代数式|x+3|+|x-2|最小值是______ ;方程|x+3|+|x-2|=7的解为 。
第二章《有理数》单元复习二(提优卷)
参考答案
一、选择题
A2.B3.A4.B5.A6.D7.A8.C9.C10.C
二、填空题
11.1 2.2或0 13.90 14.78分 15. -7或2 16.5或﹣3 17.31,35.5,24.5 18.-1;
三、解答题
19.正数集合,8, , , , …;
负数集合, , , , …;
整数集合 0 ,8 -2 …;
有理数集合,,,8,,,,,…;
无理数集合 , ….
20.(1)-7 (2) 一3 (3) (4) 一19.23 (5)
21.(1)=5×(-2)-(-3)×(-4)=-22.
(2)因为|x-2|=0,
所以x-2=0,即x=2.
所以==3×(-2)-2×14=-34.
解:∵(x+2)2+|x+y﹣1|=0,
∴x+2=0x+y-1=0,
解得x=-2y=3,
∴xy=(﹣2)3=﹣8,
即xy的值是﹣8.
23.解:(1)812 (2)28
(3)5-2-6+15-9-13+8=-2,
2×60+2×15=150(元),
1400×60-150=83850(元).
答:该厂工人这一周的工资总额是83850元.
24.(1)3n+2,602,n=673
25.28. (1)3;3;4 ;
(2) ∵|x+3|=2
∴x+3=2;3+3=-2
∴x=-1或x=-5
(3)代数式|x+3|+|x-2|最小值是 ___5_____,.
选择题
的相反数是 ( )
A. B. C. D.
下列说法正确的个数是 ( )
①一个有理数不是整数就是分数;②无限循环小数是无理数;
③一个整数不是正的,就是负的;④一个分数不是正的,就是负的.
A.1 B.2 C. 3 D. 4
下列等式成立的是 ( )
A. B. C. D.
4.(-5)6表示的意义是 ( )
A.-5乘以6的积 B.6个-5相乘的积
C.5个-6相乘的积 D.6个-5相加的和
5.下面说法:①-a一定是负数;②若|a|=|b|,则a=b;③一个有理数中不是整数就是分数;④一个有理数不是正数就是负数.其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
6.北京故宫的面积约为720 000 m2,用科学记数法表示为 ( )
A.0.72×106m2 B.7.2×106m2 C.0.72×105m2 D.7.2×105m2
7.观察下列等式,7 1=7,7 2=49,7 3=343,。74=2 401,…,由此可以判断7100的个位数字是 ( )
A.1 B.7 C.9 D.3
8.若规定“!”是一种数学运算符号,且则的值为 ( )
A. B.99! C.9 900 D.2!
9.数学家发明了一个魔术盒,当任意有理数对进入其中时,会得到一个新的有理数:+ b -.例如,把放入其中,就会得到.现将有理数对放入其中,得到有理数,再将有理数对放入其中后,得到的有理数是 ( )
A.3 B.6 C.9 D.12
10.小王用计算机设计一个程序,输入和输出的数据如下表:
输入 ··· 1 2 3 4 5 6 ···
输出 ···
···
那么输入8时,输出的数据是 ( )
A. B. C. D.
二、填空题
11.若规定,则的值为 .
12.已知|a|=1,|b|=2,|c|=3,且a>b>c,那么a+b﹣c=________.?
13.观察下面一列数:-1,2,-3,4,-5,6,-7,…,将这列数排成图2的形式,按照上述规律排下去,那么第10行从左边数第9个数是________.
某次数学测验共20道选择题,规则是:选对一道得5分,选错一道得-1分,不选得零分,王明同学的卷面成绩是:选对16道题,选错2道题,有2道题未做,他的得分是 .
15.若数轴上的点A所表示的有理数是-2,则与点A相距5个单位长度的点所表示的有理数是____________.
16.若|a﹣1|=4,则a=________.
17.股民李金上星期六买进某公司的股票,每股27元,下表为本周内该股票涨跌情况(单位:元)
星期 一 二 三 四 五 六
每股涨跌 (与前一天相比) -1.5 -1 +6.5 +3.5 +1 -4
星期三收盘时.每股是 元;本周内最高价是每股 元;最低价是每股 元.
18. 已知|a-3|+=0,则= .
三、解答题
19. 将下列各数填入相应的括号里:
,,,8,,,,,…,,.
正数集合 …;
负数集合 …;
整数集合 …;
有理数集合 …;
无理数集合 ….
20.计算:
(1) (2)
(3)
(4)
(5)
21.阅读材料:对于任何实数,我们规定符号的意义是=ad-bc.
例如:=1×4-2×3=-2,=(-2)×5-4×3=-22.
(1)按照这个规定请你计算的值;
(2)按照这个规定请你计算:当|x-2|=0时,的值.
22.小明在复习归纳时发现初中阶段学习了三个非负数,分别是:①a2;②a;③|a|(a是任意实数).于是他结合所学习的三个非负数的知识,自己编了一道题:已知(x+2)2+|x+y﹣1|=0,求xy的值.请你利用三个非负数的知识解答这个问题
23.某自行车厂7天计划生产1400辆自行车,平均每天生产200辆,由于各种原因,无法按计划生产,下表是这7天的生产情况(超产为正,减产为负,单位:辆):
第1天 第2天 第3天 第4天 第5天 第6天 第7天
+5 -2 -6 +15 -9 -13 +8
(1)根据记录可知前4天共生产自行车______辆;
(2)自行车产量最多的一天比产量最少的一天多生产________辆;
(3)该厂实行日计件工资制,每生产一辆自行车,厂方付给工人工资60元,超额完成计划任务的,每超产一辆奖励15元,没有完成计划任务的,每减产一辆扣15元,则该厂工人这7天的工资总额是多少?
24.将图①中的正方形剪开得到图②,图②中共有个正方形;将图②中一个正方形剪开得到图③,图③中共有个正方形;将图③中一个正方形剪开得到图④;;如此下去.
()按图示规律填写下表:
图 ① ② ③ ④ ⑤
正方形个数
()按照这种方式剪下去,求第个图中有多少个正方形.
()按照这种方式剪下去,求第个图中有多少个正方形.
()按照这种方式剪下去,求第几个图中有个正方形.
25若点A、B在数轴上分别表示实数a、b,则我们可以定义|a-b|为A、B两点之间的距离,表示为|AB|=|a-b|.根据这个定义回答下列问题:
(1)数轴上表示2和5的两点之间的距离是______ ,表示-2和-5的两点之间的距离是______ ;表示1和-3的两点之间的距离是______ ;表示x和-1的两点A和B之间的距离是_____ ;
(2)如果|x+3|=2,求的值;
(3)代数式|x+3|+|x-2|最小值是______ ;方程|x+3|+|x-2|=7的解为 。
第二章《有理数》单元复习二(提优卷)
参考答案
一、选择题
A2.B3.A4.B5.A6.D7.A8.C9.C10.C
二、填空题
11.1 2.2或0 13.90 14.78分 15. -7或2 16.5或﹣3 17.31,35.5,24.5 18.-1;
三、解答题
19.正数集合,8, , , , …;
负数集合, , , , …;
整数集合 0 ,8 -2 …;
有理数集合,,,8,,,,,…;
无理数集合 , ….
20.(1)-7 (2) 一3 (3) (4) 一19.23 (5)
21.(1)=5×(-2)-(-3)×(-4)=-22.
(2)因为|x-2|=0,
所以x-2=0,即x=2.
所以==3×(-2)-2×14=-34.
解:∵(x+2)2+|x+y﹣1|=0,
∴x+2=0x+y-1=0,
解得x=-2y=3,
∴xy=(﹣2)3=﹣8,
即xy的值是﹣8.
23.解:(1)812 (2)28
(3)5-2-6+15-9-13+8=-2,
2×60+2×15=150(元),
1400×60-150=83850(元).
答:该厂工人这一周的工资总额是83850元.
24.(1)3n+2,602,n=673
25.28. (1)3;3;4 ;
(2) ∵|x+3|=2
∴x+3=2;3+3=-2
∴x=-1或x=-5
(3)代数式|x+3|+|x-2|最小值是 ___5_____,.
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
