人教版数学八年级下册 第18章 平行四边形单元测试试题(一)(word版含解析)
文档属性
| 名称 | 人教版数学八年级下册 第18章 平行四边形单元测试试题(一)(word版含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 286.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-03 00:00:00 | ||
图片预览


文档简介
平行四边形单元测试试题(一)
一.选择题
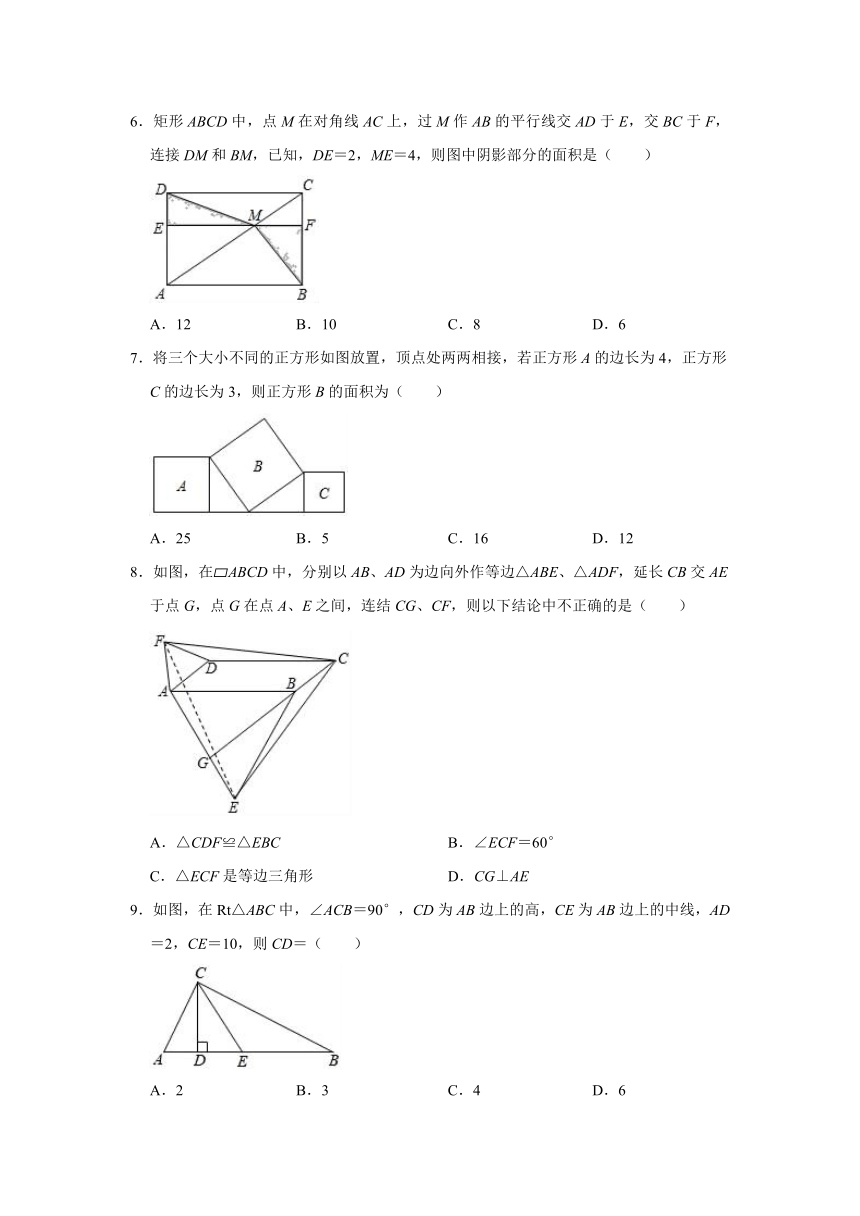
1.在平行四边形ABCD中,若∠A=60°,则∠B的度数是( )
A.30°
B.60°
C.90°
D.120°
2.如图,在菱形ABCD中,AB的垂直平分线交对角线AC于点F,垂足为E,连结DF,若∠BAD=70°,则∠CFD等于( )
A.50°
B.60°
C.70°
D.80°
3.如图,菱形ABCD的边长为,对角线AC,BD交于点O,OA=1,则菱形ABCD的面积为( )
A.
B.2
C.2
D.4
4.下列说法中错误的是( )
A.对角线互相平分的四边形是菱形
B.对角线相等的平行四边形是矩形
C.菱形的对角线互相垂直
D.对角线长为a的正方形的面积是
5.如图,两个全等的矩形纸片重叠在一起,矩形的长和宽分别是8和6,则重叠部分的四边形周长是( )
A.10
B.15
C.20
D.25
6.矩形ABCD中,点M在对角线AC上,过M作AB的平行线交AD于E,交BC于F,连接DM和BM,已知,DE=2,ME=4,则图中阴影部分的面积是( )
A.12
B.10
C.8
D.6
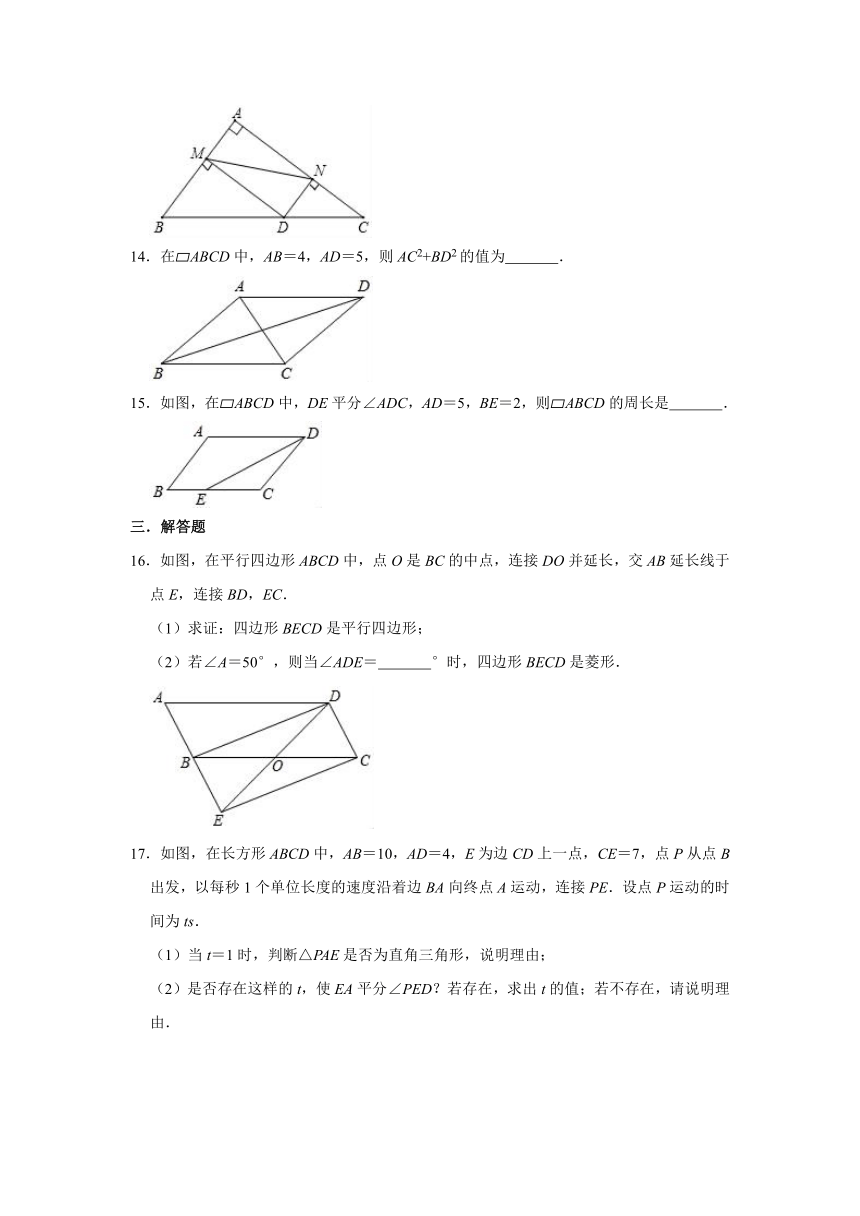
7.将三个大小不同的正方形如图放置,顶点处两两相接,若正方形A的边长为4,正方形C的边长为3,则正方形B的面积为( )
A.25
B.5
C.16
D.12
8.如图,在?ABCD中,分别以AB、AD为边向外作等边△ABE、△ADF,延长CB交AE于点G,点G在点A、E之间,连结CG、CF,则以下结论中不正确的是( )
A.△CDF≌△EBC
B.∠ECF=60°
C.△ECF是等边三角形
D.CG⊥AE
9.如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的高,CE为AB边上的中线,AD=2,CE=10,则CD=( )
A.2
B.3
C.4
D.6
10.如图,在△ABC中,∠C=90°,点D在斜边AB上,且AD=CD,则下列结论中错误的结论是( )
A.∠DCB=∠B
B.BC=BD
C.AD=BD
D.∠ACD=∠BDC
二.填空题
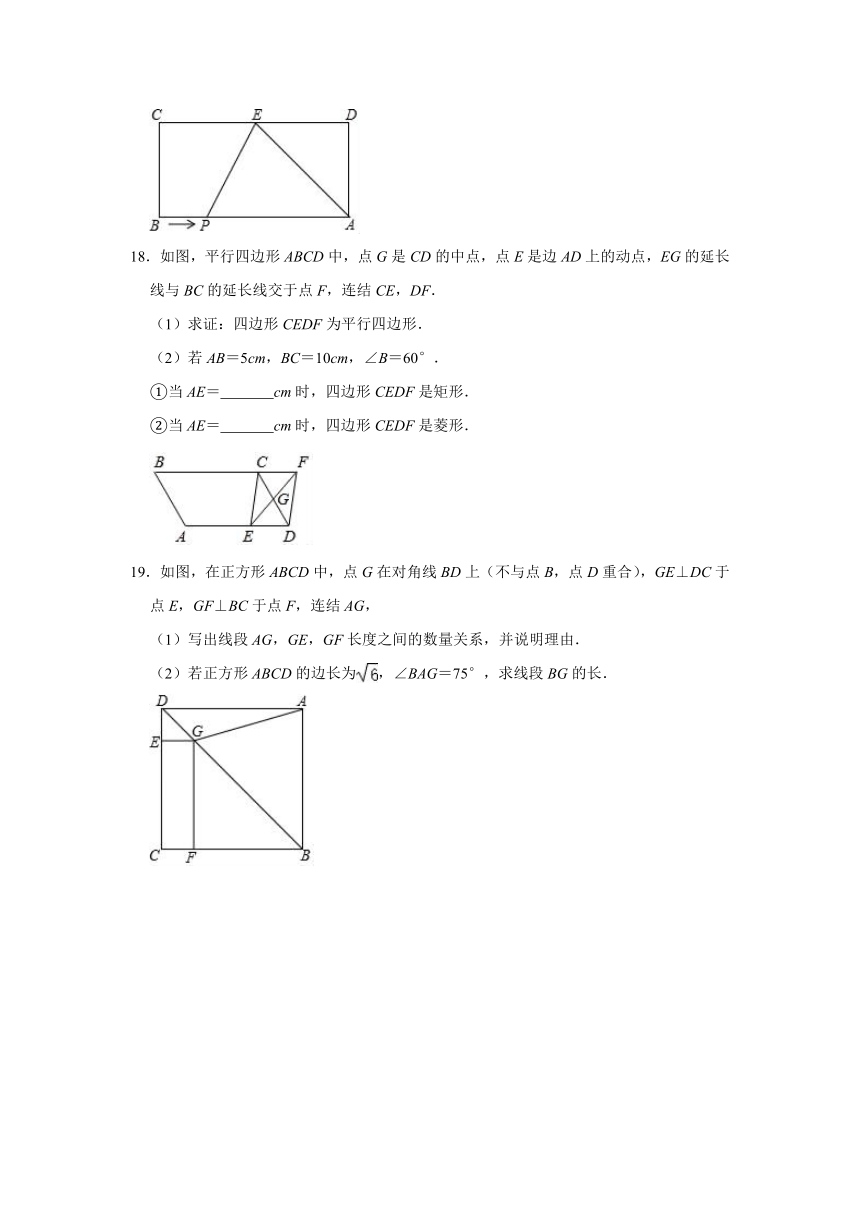
11.如图,在菱形ABCD中,对角线AC,BD相交于点O,H为BC中点,AC=6,BD=8,则线段OH的长为
.
12.如图,F是菱形ABCD的边AD的中点,AC与BF相交于E,EG⊥AB于G,已知∠1=∠2,则下列结论:①AE=BE;②BF⊥AD;③AC=2BF;④CE=BF+BG.其中正确的结论是
.
13.如图,在Rt△ABC中,∠BAC=90°,BA=5,AC=8,D是斜边BC上的一个动点,过点D分别作DM⊥AB于点M,DN⊥AC于点N,连接MN,则线段MN长的最小值为
.
14.在?ABCD中,AB=4,AD=5,则AC2+BD2的值为
.
15.如图,在?ABCD中,DE平分∠ADC,AD=5,BE=2,则?ABCD的周长是
.
三.解答题
16.如图,在平行四边形ABCD中,点O是BC的中点,连接DO并延长,交AB延长线于点E,连接BD,EC.
(1)求证:四边形BECD是平行四边形;
(2)若∠A=50°,则当∠ADE=
°时,四边形BECD是菱形.
17.如图,在长方形ABCD中,AB=10,AD=4,E为边CD上一点,CE=7,点P从点B出发,以每秒1个单位长度的速度沿着边BA向终点A运动,连接PE.设点P运动的时间为ts.
(1)当t=1时,判断△PAE是否为直角三角形,说明理由;
(2)是否存在这样的t,使EA平分∠PED?若存在,求出t的值;若不存在,请说明理由.
18.如图,平行四边形ABCD中,点G是CD的中点,点E是边AD上的动点,EG的延长线与BC的延长线交于点F,连结CE,DF.
(1)求证:四边形CEDF为平行四边形.
(2)若AB=5cm,BC=10cm,∠B=60°.
①当AE=
cm时,四边形CEDF是矩形.
②当AE=
cm时,四边形CEDF是菱形.
19.如图,在正方形ABCD中,点G在对角线BD上(不与点B,点D重合),GE⊥DC于点E,GF⊥BC于点F,连结AG,
(1)写出线段AG,GE,GF长度之间的数量关系,并说明理由.
(2)若正方形ABCD的边长为,∠BAG=75°,求线段BG的长.
参考答案与试题解析
一.选择题
1.【解答】解:如图,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠A+∠B=180°,
∴∠B=180°﹣60°=120°.
故选:D.
2.【解答】解:连接BF,如图所示:
∵四边形ABCD是菱形,
∴∠BAC=∠BAD=×70°=35°,∠BCF=∠DCF=∠BAC,BC=DC,∠ABC=180°﹣∠BAD=180°﹣70°=110°,
∵EF是线段AB的垂直平分线,
∴AF=BF,
∴∠DCF=∠ABF=∠BAC=35°,
∴∠CBF=∠ABC﹣∠ABF=110°﹣35°=75°,
在△BCF和△DCF中,
,
∴△BCF≌△DCF(SAS),
∴∠CDF=∠CBF=75°,
∴∠CFD=180°﹣∠CDF﹣∠DCF=180°﹣75°﹣35°=70°,
故选:C.
3.【解答】解:∵对角线AC,BD交于点O,OA=1,
∴AC=2AO=2,
∵菱形ABCD的边长为,
∴AB=,
∴BO===2,
∴BD=2BO=4,
∴菱形ABCD的面积=BD×AC==4,
故选:D.
4.【解答】解:因为对角线互相平分的四边形是平行四边形,所以A选项错误,符合题意;
因为对角线相等的平行四边形是矩形,所以B选项正确,不符合题意;
因为菱形的对角线互相垂直,所以C选项正确,不符合题意;
因为对角线长为a的正方形的面积是:
a×a=a2.所以D选项正确,不符合题意.
故选:A.
5.【解答】解:如图所示:
由题意得:矩形BFDE≌矩形BHDG,
∴∠G=90°,DG=DE=6,BG∥DH,BE∥DF,BG=8,
∴四边形ABCD平行四边形,
∴平行四边形ABCD的面积=AD×DG=CD×DE,
∴AD=CD,
∴四边形ABCD是菱形,
∴CD=BC=AB=AD,
设CD=BC=x,则CG=8﹣x,
在Rt△CDG中,由勾股定理得:62+(8﹣x)2=x2,
解得:x=,
∴CD=,
∴四边形ABCD的周长=4CD=25;
故选:D.
6.【解答】解:过M作MP⊥AB于P,交DC于Q,如图所示:
则四边形DEMQ,四边形QMFC,四边形AEMP,四边形MPBF都是矩形,
∴S△DEM=S△DQM,S△QCM=S△MFC,S△AEM=S△APM,S△MPB=S△MFB,S△ABC=S△ADC,
∴S△ABC﹣S△AMP﹣S△MCF=S△ADC﹣S△AEM﹣S△MQC,
∴S四边形DEMQ=S四边形MPBF,
∵DE=CF=2,
∴S△DEM=S△MFB=×2×4=4,
∴S阴=4+4=8,
故选:C.
7.【解答】解:如图,
∵根据正方形的性质得:DF=FG,∠DEF=∠GHF=∠DFG=90°,
∴∠EDF+∠DFE=90°,∠DFE+∠GFH=90°,
∴∠EDF=∠GFH,
在△DEF和△FHG中,
,
∴△DEF≌△FHG(AAS),
∴DE=FH=4,
∵GH=3,
在Rt△GHF中,由勾股定理得:FG2=32+42=25,
则正方形B的面积为25.
故选:A.
8.【解答】解:∵△ABE、△ADF是等边三角形,
∴FD=AD,BE=AB,
∵AD=BC,AB=DC,
∴FD=BC,BE=DC,
∵∠CBE=∠FDC,∠FDA=∠ABE,
∴∠CDF=∠EB,
∴△CDF≌△EBC(SAS),故A正确;
∵∠FAE=∠FAD+∠EAB+∠BAD=60°+60°+(180°﹣∠CDA)=300°﹣∠CDA,
∠FDC=360°﹣∠FDA﹣∠ADC=300°﹣∠CDA,
∴∠CDF=∠EAF,
同理可得:∠CBE=∠EAF=∠CDF,
∵BC=AD=AF,BE=AE,
∴△EAF≌△EBC(SAS),
∴∠AEF=∠BEC,
∵∠AEF+∠FEB=∠BEC+∠FEB=∠AEB=60°,
∴∠FEC=60°,
∵CF=CE,
∴△ECF是等边三角形,故C正确;
∴∠ECF=60°,故B正确;
在等边三角形ABE中,
∵等边三角形顶角平分线、底边上的中线、高和垂直平分线是同一条线段,
∴如果CG⊥AE,则G是AE的中点,
∴∠ABG=30°,∠ABC=150°,
而题目缺少这个条件,
∴CG⊥AE不能求证,故D错误.
故选:D.
9.【解答】解:在Rt△ABC中,∠ACB=90°,CE为AB边上的中线,CE=10,
∴AE=CE=10,
∵AD=4,
∴DE=6,
∵CD为AB边上的高,
在Rt△CDE中,CD===6,
故选:D.
10.【解答】解:∵∠C=90°,
∴∠A+∠B=90°,∠ACD+∠BCD=90°,
∵AD=CD,
∴∠A=∠ACD,
∴∠B=∠BCD,A选项结论正确,不符合题意;
BC与BD不一定相等,B选项结论错误,符合题意;
∵∠B=∠BCD,
∴BD=CD,
∵AD=CD,
∴AD=BD,C选项结论正确,不符合题意;
∵∠A=∠ACD,
∴∠BDC=∠A=∠ACD=2∠ACD,
∴∠ACD=∠BDC,D选项结论正确,不符合题意;
故选:B.
二.填空题(共5小题)
11.【解答】解:∵四边形ABCD为菱形,
∴AC⊥BD,OB=OD=BD=4,OC=OA=AC=3,
在Rt△BOC中,BC==5,
∵H为BC中点,
∴OH=BC=2.5.
故答案为:2.5.
12.【解答】解:连接DB交AC于O,
∵四边形ABCD为菱形,
∴AD∥CB,AD=AB,AC⊥BD,AO=CO,∠DAC=∠CAB,
∴∠1=∠DAC,∠1=∠2,
∴∠CAB=∠2,
∴AE=BE,
故①正确;
∵AE=BE,EG⊥AB,
∴AG=GB=AB,
∵F是AD中点,
∴AF=AD,
∴AF=AG,
在△AEF与△AEG中,
,
∴△AEF≌△AEG(SAS),
∴∠AFE=∠AEG=90°,
∴BF⊥AD,
故②正确;
在△AFB与△ABO中,
,
∴△AFB≌△ABO(AAS),
∴BF=AO=AC,
∴AC=2BF,
故③正确;
∵∠2+∠CAB+∠CAD=90°,∠2=∠CAB=∠CAD,
∴∠2=∠CAB=∠CAD=30°,
∴BO=AB=BG,
在Rt△EGB与Rt△EOB中,
,
∴Rt△EGB≌Rt△EOB(HL),
∴EG=EO,
∴CE=CO+EO=BF+EG,
故④错误.
故答案为:①②③.
13.【解答】解:∵∠BAC=90°,且BA=5,AC=8,
∴BC===,
∵DM⊥AB,DN⊥AC,
∴∠DMA=∠DNA=∠BAC=90°,
∴四边形DMAN是矩形,
∴MN=AD,
∴当AD⊥BC时,AD的值最小,
此时,△ABC的面积=AB×AC=BC×AD,
∴AD===,
∴MN的最小值为,
故答案为:.
14.【解答】解:过点A作AE⊥BC于E,过点D作DF⊥BC于F,
设BE=CF=x,AE=DF=y,
则
AC2+BD2
=(5﹣x)2+y2+(5+x)2+y2
=50+2x2+2y2
=50+2×42
=82.
故答案为:82.
15.【解答】解:∵DE平分∠ADC,
∴∠ADE=∠CDE,
∵?ABCD中,
∴AD∥BC,
∴∠ADE=∠CED,
∴∠CDE=∠CED,
∴CE=CD,
在?ABCD中,AD=5,BE=2,
∴AD=BC=5,
∴CE=BC﹣BE=5﹣2=5,
∴CD=AB=5,
∴?ABCD的周长=5+5+3+3=16,
故答案为:16.
三.解答题(共4小题)
16.【解答】(1)证明:∵四边形ABCD为平行四边形,
∴AB∥DC,AB=CD,
∴∠OEB=∠ODC,
又∵O为BC的中点,
∴BO=CO,
在△BOE和△COD中,
,
∴△BOE≌△COD(AAS);
∴OE=OD,
∴四边形BECD是平行四边形;
(2)解:当∠ADE=90°时,四边形BECD是菱形,理由如下:
∵∠A=50°,∠ADE=90°,
∴∠AED=40°,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠CBE=∠A=50°,
∴∠BOE=90°,
∴BC⊥DE,
∴四边形BECD是菱形,
故答案为:90.
17.【解答】解:(1)过点P作PF⊥CD于点F,如图:
由题意得BP=t,AP=10﹣t,PF=4,EF=7﹣t.
当t=1时,△PAE不是直角三角形,理由如下:
当t=1时,
PE2=PF2+EF2=42+(7﹣t)2=16+36=52,AP2=(10﹣t)2=81,
∵在长方形ABCD中,AB=10,CE=7,
∴DC=AB=10,
∴DE=DC﹣CE=10﹣7=3,
又AD=4,
∴AE2=32+42=25,
∵81≠52+25,
∴AP2≠PE2+EA2,
∴△PAE不是直角三角形;
(2)存在这样的t,使EA平分∠PED,理由如下:
若EA平分∠PED,则∠AED=∠PEA,
∵四边形ABCD为长方形,
∴CD∥AB,
∴∠AED=∠EAP,
∴∠PEA=∠EAP,
∴PE=PA=10﹣t,
∵PF⊥CD,
∴∠PFD=90°,
又∵在长方形ABCD中,∠D=∠DAB=90°,
∴四边形PADF为长方形,
∴PF=AD=4,
在Rt△PEF中,EP2=EF2+PF2,
∴(10﹣t)2=42+(7﹣t)2,
解得:t=.
18.【解答】(1)证明:∵四边形ABCD是平行四边形
∴AD∥BF,
∴∠DEG=∠CFG,
∵G是CD的中点,
∴GD=GC,
在△GED和△GFC中,
,
∴△GED≌△GFC(AAS),
∴DE=CF,
又∵DE∥CF,
∴四边形CEDF是平行四边形,
(2)解:①当AE=7.5cm时,四边形CEDF是矩形;理由如下:
作AP⊥BC于P,如图所示:
∵AB=6cm,∠B=60°,
∴∠BAP=30°,
∴BP=AB=2.5cm,
∵四边形ABCD是平行四边形,
∴∠CDE=∠B=60°,DC=AB=5cm,AD=BC=10cm,
∵AE=7.5cm,
∴DE=AD﹣AE=2.5cm=BP,
在△ABP和△CDE中,
,
∴△ABP≌△CDE(SAS),
∴∠CED=∠APB=90°,
∴平行四边形CEDF是矩形,
故答案为:7.5;
②当AE=5cm时,四边形CEDF是菱形,理由如下:
∵AE=5cm,AD=10cm,
∴DE=AD﹣AE=5(cm),
∵DC=5cm,∠CDE=∠B=60°,
∴△CDE是等边三角形,
∴DE=CE,
∴平行四边形CEDF是菱形,
故答案为:2cm.
19.【解答】解:(1)结论:AG2=GE2+GF2.
理由:连接CG.
∵四边形ABCD是正方形,
∴A、C关于对角线BD对称,
∵点G在BD上,
∴GA=GC,
∵GE⊥DC于点E,GF⊥BC于点F,
∴∠GEC=∠ECF=∠CFG=90°,
∴四边形EGFC是矩形,
∴CF=GE,
在Rt△GFC中,∵CG2=GF2+CF2,
∴AG2=GF2+GE2;
(2)过点A作AH⊥BG于H,
∵四边形ABCD是正方形,
∴∠ABD=∠GBF=45°,
∵GF⊥BC,
∴∠BGF=45°,
∵∠BAG=75°,
∴∠AGB=180°﹣∠ABD﹣∠BAG=60°,
∴∠GAH=30°,
在Rt△ABH中,∵AB=,
∴AH2=BH2==3,
∴AH=BH=,
在Rt△AGH中,∵AH=,∠GAH=30°,
∴AG=2HG,
∵AG2=HG2+AH2,
∴(2HG)2=HG2+()2,
解得:HG=1,
∴BG=BH+HG=+1.
一.选择题
1.在平行四边形ABCD中,若∠A=60°,则∠B的度数是( )
A.30°
B.60°
C.90°
D.120°
2.如图,在菱形ABCD中,AB的垂直平分线交对角线AC于点F,垂足为E,连结DF,若∠BAD=70°,则∠CFD等于( )
A.50°
B.60°
C.70°
D.80°
3.如图,菱形ABCD的边长为,对角线AC,BD交于点O,OA=1,则菱形ABCD的面积为( )
A.
B.2
C.2
D.4
4.下列说法中错误的是( )
A.对角线互相平分的四边形是菱形
B.对角线相等的平行四边形是矩形
C.菱形的对角线互相垂直
D.对角线长为a的正方形的面积是
5.如图,两个全等的矩形纸片重叠在一起,矩形的长和宽分别是8和6,则重叠部分的四边形周长是( )
A.10
B.15
C.20
D.25
6.矩形ABCD中,点M在对角线AC上,过M作AB的平行线交AD于E,交BC于F,连接DM和BM,已知,DE=2,ME=4,则图中阴影部分的面积是( )
A.12
B.10
C.8
D.6
7.将三个大小不同的正方形如图放置,顶点处两两相接,若正方形A的边长为4,正方形C的边长为3,则正方形B的面积为( )
A.25
B.5
C.16
D.12
8.如图,在?ABCD中,分别以AB、AD为边向外作等边△ABE、△ADF,延长CB交AE于点G,点G在点A、E之间,连结CG、CF,则以下结论中不正确的是( )
A.△CDF≌△EBC
B.∠ECF=60°
C.△ECF是等边三角形
D.CG⊥AE
9.如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的高,CE为AB边上的中线,AD=2,CE=10,则CD=( )
A.2
B.3
C.4
D.6
10.如图,在△ABC中,∠C=90°,点D在斜边AB上,且AD=CD,则下列结论中错误的结论是( )
A.∠DCB=∠B
B.BC=BD
C.AD=BD
D.∠ACD=∠BDC
二.填空题
11.如图,在菱形ABCD中,对角线AC,BD相交于点O,H为BC中点,AC=6,BD=8,则线段OH的长为
.
12.如图,F是菱形ABCD的边AD的中点,AC与BF相交于E,EG⊥AB于G,已知∠1=∠2,则下列结论:①AE=BE;②BF⊥AD;③AC=2BF;④CE=BF+BG.其中正确的结论是
.
13.如图,在Rt△ABC中,∠BAC=90°,BA=5,AC=8,D是斜边BC上的一个动点,过点D分别作DM⊥AB于点M,DN⊥AC于点N,连接MN,则线段MN长的最小值为
.
14.在?ABCD中,AB=4,AD=5,则AC2+BD2的值为
.
15.如图,在?ABCD中,DE平分∠ADC,AD=5,BE=2,则?ABCD的周长是
.
三.解答题
16.如图,在平行四边形ABCD中,点O是BC的中点,连接DO并延长,交AB延长线于点E,连接BD,EC.
(1)求证:四边形BECD是平行四边形;
(2)若∠A=50°,则当∠ADE=
°时,四边形BECD是菱形.
17.如图,在长方形ABCD中,AB=10,AD=4,E为边CD上一点,CE=7,点P从点B出发,以每秒1个单位长度的速度沿着边BA向终点A运动,连接PE.设点P运动的时间为ts.
(1)当t=1时,判断△PAE是否为直角三角形,说明理由;
(2)是否存在这样的t,使EA平分∠PED?若存在,求出t的值;若不存在,请说明理由.
18.如图,平行四边形ABCD中,点G是CD的中点,点E是边AD上的动点,EG的延长线与BC的延长线交于点F,连结CE,DF.
(1)求证:四边形CEDF为平行四边形.
(2)若AB=5cm,BC=10cm,∠B=60°.
①当AE=
cm时,四边形CEDF是矩形.
②当AE=
cm时,四边形CEDF是菱形.
19.如图,在正方形ABCD中,点G在对角线BD上(不与点B,点D重合),GE⊥DC于点E,GF⊥BC于点F,连结AG,
(1)写出线段AG,GE,GF长度之间的数量关系,并说明理由.
(2)若正方形ABCD的边长为,∠BAG=75°,求线段BG的长.
参考答案与试题解析
一.选择题
1.【解答】解:如图,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠A+∠B=180°,
∴∠B=180°﹣60°=120°.
故选:D.
2.【解答】解:连接BF,如图所示:
∵四边形ABCD是菱形,
∴∠BAC=∠BAD=×70°=35°,∠BCF=∠DCF=∠BAC,BC=DC,∠ABC=180°﹣∠BAD=180°﹣70°=110°,
∵EF是线段AB的垂直平分线,
∴AF=BF,
∴∠DCF=∠ABF=∠BAC=35°,
∴∠CBF=∠ABC﹣∠ABF=110°﹣35°=75°,
在△BCF和△DCF中,
,
∴△BCF≌△DCF(SAS),
∴∠CDF=∠CBF=75°,
∴∠CFD=180°﹣∠CDF﹣∠DCF=180°﹣75°﹣35°=70°,
故选:C.
3.【解答】解:∵对角线AC,BD交于点O,OA=1,
∴AC=2AO=2,
∵菱形ABCD的边长为,
∴AB=,
∴BO===2,
∴BD=2BO=4,
∴菱形ABCD的面积=BD×AC==4,
故选:D.
4.【解答】解:因为对角线互相平分的四边形是平行四边形,所以A选项错误,符合题意;
因为对角线相等的平行四边形是矩形,所以B选项正确,不符合题意;
因为菱形的对角线互相垂直,所以C选项正确,不符合题意;
因为对角线长为a的正方形的面积是:
a×a=a2.所以D选项正确,不符合题意.
故选:A.
5.【解答】解:如图所示:
由题意得:矩形BFDE≌矩形BHDG,
∴∠G=90°,DG=DE=6,BG∥DH,BE∥DF,BG=8,
∴四边形ABCD平行四边形,
∴平行四边形ABCD的面积=AD×DG=CD×DE,
∴AD=CD,
∴四边形ABCD是菱形,
∴CD=BC=AB=AD,
设CD=BC=x,则CG=8﹣x,
在Rt△CDG中,由勾股定理得:62+(8﹣x)2=x2,
解得:x=,
∴CD=,
∴四边形ABCD的周长=4CD=25;
故选:D.
6.【解答】解:过M作MP⊥AB于P,交DC于Q,如图所示:
则四边形DEMQ,四边形QMFC,四边形AEMP,四边形MPBF都是矩形,
∴S△DEM=S△DQM,S△QCM=S△MFC,S△AEM=S△APM,S△MPB=S△MFB,S△ABC=S△ADC,
∴S△ABC﹣S△AMP﹣S△MCF=S△ADC﹣S△AEM﹣S△MQC,
∴S四边形DEMQ=S四边形MPBF,
∵DE=CF=2,
∴S△DEM=S△MFB=×2×4=4,
∴S阴=4+4=8,
故选:C.
7.【解答】解:如图,
∵根据正方形的性质得:DF=FG,∠DEF=∠GHF=∠DFG=90°,
∴∠EDF+∠DFE=90°,∠DFE+∠GFH=90°,
∴∠EDF=∠GFH,
在△DEF和△FHG中,
,
∴△DEF≌△FHG(AAS),
∴DE=FH=4,
∵GH=3,
在Rt△GHF中,由勾股定理得:FG2=32+42=25,
则正方形B的面积为25.
故选:A.
8.【解答】解:∵△ABE、△ADF是等边三角形,
∴FD=AD,BE=AB,
∵AD=BC,AB=DC,
∴FD=BC,BE=DC,
∵∠CBE=∠FDC,∠FDA=∠ABE,
∴∠CDF=∠EB,
∴△CDF≌△EBC(SAS),故A正确;
∵∠FAE=∠FAD+∠EAB+∠BAD=60°+60°+(180°﹣∠CDA)=300°﹣∠CDA,
∠FDC=360°﹣∠FDA﹣∠ADC=300°﹣∠CDA,
∴∠CDF=∠EAF,
同理可得:∠CBE=∠EAF=∠CDF,
∵BC=AD=AF,BE=AE,
∴△EAF≌△EBC(SAS),
∴∠AEF=∠BEC,
∵∠AEF+∠FEB=∠BEC+∠FEB=∠AEB=60°,
∴∠FEC=60°,
∵CF=CE,
∴△ECF是等边三角形,故C正确;
∴∠ECF=60°,故B正确;
在等边三角形ABE中,
∵等边三角形顶角平分线、底边上的中线、高和垂直平分线是同一条线段,
∴如果CG⊥AE,则G是AE的中点,
∴∠ABG=30°,∠ABC=150°,
而题目缺少这个条件,
∴CG⊥AE不能求证,故D错误.
故选:D.
9.【解答】解:在Rt△ABC中,∠ACB=90°,CE为AB边上的中线,CE=10,
∴AE=CE=10,
∵AD=4,
∴DE=6,
∵CD为AB边上的高,
在Rt△CDE中,CD===6,
故选:D.
10.【解答】解:∵∠C=90°,
∴∠A+∠B=90°,∠ACD+∠BCD=90°,
∵AD=CD,
∴∠A=∠ACD,
∴∠B=∠BCD,A选项结论正确,不符合题意;
BC与BD不一定相等,B选项结论错误,符合题意;
∵∠B=∠BCD,
∴BD=CD,
∵AD=CD,
∴AD=BD,C选项结论正确,不符合题意;
∵∠A=∠ACD,
∴∠BDC=∠A=∠ACD=2∠ACD,
∴∠ACD=∠BDC,D选项结论正确,不符合题意;
故选:B.
二.填空题(共5小题)
11.【解答】解:∵四边形ABCD为菱形,
∴AC⊥BD,OB=OD=BD=4,OC=OA=AC=3,
在Rt△BOC中,BC==5,
∵H为BC中点,
∴OH=BC=2.5.
故答案为:2.5.
12.【解答】解:连接DB交AC于O,
∵四边形ABCD为菱形,
∴AD∥CB,AD=AB,AC⊥BD,AO=CO,∠DAC=∠CAB,
∴∠1=∠DAC,∠1=∠2,
∴∠CAB=∠2,
∴AE=BE,
故①正确;
∵AE=BE,EG⊥AB,
∴AG=GB=AB,
∵F是AD中点,
∴AF=AD,
∴AF=AG,
在△AEF与△AEG中,
,
∴△AEF≌△AEG(SAS),
∴∠AFE=∠AEG=90°,
∴BF⊥AD,
故②正确;
在△AFB与△ABO中,
,
∴△AFB≌△ABO(AAS),
∴BF=AO=AC,
∴AC=2BF,
故③正确;
∵∠2+∠CAB+∠CAD=90°,∠2=∠CAB=∠CAD,
∴∠2=∠CAB=∠CAD=30°,
∴BO=AB=BG,
在Rt△EGB与Rt△EOB中,
,
∴Rt△EGB≌Rt△EOB(HL),
∴EG=EO,
∴CE=CO+EO=BF+EG,
故④错误.
故答案为:①②③.
13.【解答】解:∵∠BAC=90°,且BA=5,AC=8,
∴BC===,
∵DM⊥AB,DN⊥AC,
∴∠DMA=∠DNA=∠BAC=90°,
∴四边形DMAN是矩形,
∴MN=AD,
∴当AD⊥BC时,AD的值最小,
此时,△ABC的面积=AB×AC=BC×AD,
∴AD===,
∴MN的最小值为,
故答案为:.
14.【解答】解:过点A作AE⊥BC于E,过点D作DF⊥BC于F,
设BE=CF=x,AE=DF=y,
则
AC2+BD2
=(5﹣x)2+y2+(5+x)2+y2
=50+2x2+2y2
=50+2×42
=82.
故答案为:82.
15.【解答】解:∵DE平分∠ADC,
∴∠ADE=∠CDE,
∵?ABCD中,
∴AD∥BC,
∴∠ADE=∠CED,
∴∠CDE=∠CED,
∴CE=CD,
在?ABCD中,AD=5,BE=2,
∴AD=BC=5,
∴CE=BC﹣BE=5﹣2=5,
∴CD=AB=5,
∴?ABCD的周长=5+5+3+3=16,
故答案为:16.
三.解答题(共4小题)
16.【解答】(1)证明:∵四边形ABCD为平行四边形,
∴AB∥DC,AB=CD,
∴∠OEB=∠ODC,
又∵O为BC的中点,
∴BO=CO,
在△BOE和△COD中,
,
∴△BOE≌△COD(AAS);
∴OE=OD,
∴四边形BECD是平行四边形;
(2)解:当∠ADE=90°时,四边形BECD是菱形,理由如下:
∵∠A=50°,∠ADE=90°,
∴∠AED=40°,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠CBE=∠A=50°,
∴∠BOE=90°,
∴BC⊥DE,
∴四边形BECD是菱形,
故答案为:90.
17.【解答】解:(1)过点P作PF⊥CD于点F,如图:
由题意得BP=t,AP=10﹣t,PF=4,EF=7﹣t.
当t=1时,△PAE不是直角三角形,理由如下:
当t=1时,
PE2=PF2+EF2=42+(7﹣t)2=16+36=52,AP2=(10﹣t)2=81,
∵在长方形ABCD中,AB=10,CE=7,
∴DC=AB=10,
∴DE=DC﹣CE=10﹣7=3,
又AD=4,
∴AE2=32+42=25,
∵81≠52+25,
∴AP2≠PE2+EA2,
∴△PAE不是直角三角形;
(2)存在这样的t,使EA平分∠PED,理由如下:
若EA平分∠PED,则∠AED=∠PEA,
∵四边形ABCD为长方形,
∴CD∥AB,
∴∠AED=∠EAP,
∴∠PEA=∠EAP,
∴PE=PA=10﹣t,
∵PF⊥CD,
∴∠PFD=90°,
又∵在长方形ABCD中,∠D=∠DAB=90°,
∴四边形PADF为长方形,
∴PF=AD=4,
在Rt△PEF中,EP2=EF2+PF2,
∴(10﹣t)2=42+(7﹣t)2,
解得:t=.
18.【解答】(1)证明:∵四边形ABCD是平行四边形
∴AD∥BF,
∴∠DEG=∠CFG,
∵G是CD的中点,
∴GD=GC,
在△GED和△GFC中,
,
∴△GED≌△GFC(AAS),
∴DE=CF,
又∵DE∥CF,
∴四边形CEDF是平行四边形,
(2)解:①当AE=7.5cm时,四边形CEDF是矩形;理由如下:
作AP⊥BC于P,如图所示:
∵AB=6cm,∠B=60°,
∴∠BAP=30°,
∴BP=AB=2.5cm,
∵四边形ABCD是平行四边形,
∴∠CDE=∠B=60°,DC=AB=5cm,AD=BC=10cm,
∵AE=7.5cm,
∴DE=AD﹣AE=2.5cm=BP,
在△ABP和△CDE中,
,
∴△ABP≌△CDE(SAS),
∴∠CED=∠APB=90°,
∴平行四边形CEDF是矩形,
故答案为:7.5;
②当AE=5cm时,四边形CEDF是菱形,理由如下:
∵AE=5cm,AD=10cm,
∴DE=AD﹣AE=5(cm),
∵DC=5cm,∠CDE=∠B=60°,
∴△CDE是等边三角形,
∴DE=CE,
∴平行四边形CEDF是菱形,
故答案为:2cm.
19.【解答】解:(1)结论:AG2=GE2+GF2.
理由:连接CG.
∵四边形ABCD是正方形,
∴A、C关于对角线BD对称,
∵点G在BD上,
∴GA=GC,
∵GE⊥DC于点E,GF⊥BC于点F,
∴∠GEC=∠ECF=∠CFG=90°,
∴四边形EGFC是矩形,
∴CF=GE,
在Rt△GFC中,∵CG2=GF2+CF2,
∴AG2=GF2+GE2;
(2)过点A作AH⊥BG于H,
∵四边形ABCD是正方形,
∴∠ABD=∠GBF=45°,
∵GF⊥BC,
∴∠BGF=45°,
∵∠BAG=75°,
∴∠AGB=180°﹣∠ABD﹣∠BAG=60°,
∴∠GAH=30°,
在Rt△ABH中,∵AB=,
∴AH2=BH2==3,
∴AH=BH=,
在Rt△AGH中,∵AH=,∠GAH=30°,
∴AG=2HG,
∵AG2=HG2+AH2,
∴(2HG)2=HG2+()2,
解得:HG=1,
∴BG=BH+HG=+1.
