人教版八年级数学上册 课件12.2三角形全等的判定 全等三角形的判定SAS(共21张ppt)
文档属性
| 名称 | 人教版八年级数学上册 课件12.2三角形全等的判定 全等三角形的判定SAS(共21张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 233.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-03 20:57:35 | ||
图片预览



文档简介
(共21张PPT)
全等三角形的判定2
边角边公理
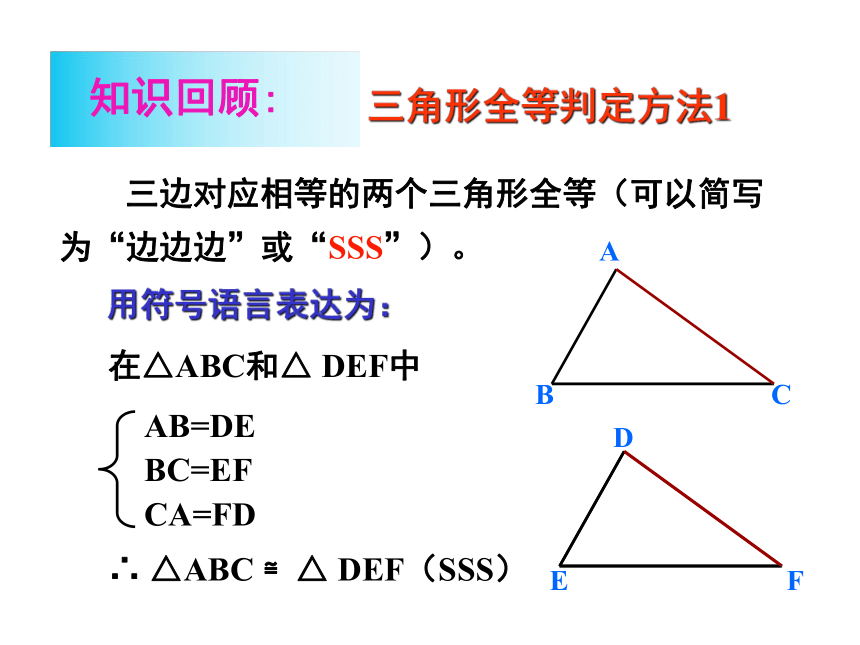
三边对应相等的两个三角形全等(可以简写为“边边边”或“SSS”)。
A
B
C
D
E
F
在△ABC和△
DEF中
∴
△ABC
≌△
DEF(SSS)
AB=DE
BC=EF
CA=FD
用符号语言表达为:
三角形全等判定方法1
知识回顾:
除了SSS外,还有其他情况吗?继续探索三角形全等的条件.
思考
(2)
三条边
(1)
三个角
(3)
两边一角
(4)
两角一边
当两个三角形满足六个条件中的三个时,有四种情况:
SSS
不能!
?
继续探讨三角形全等的条件:
两边一角
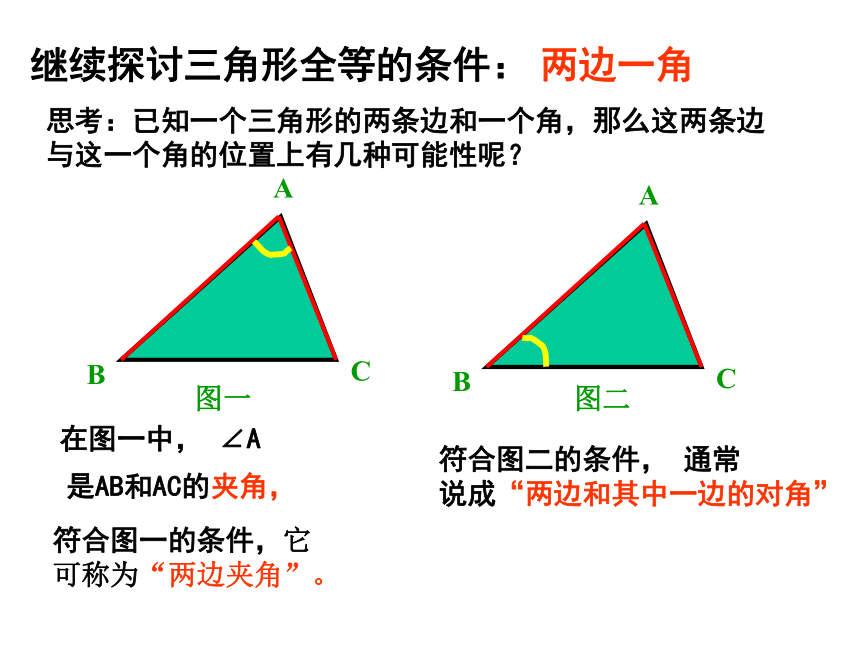
思考:已知一个三角形的两条边和一个角,那么这两条边
与这一个角的位置上有几种可能性呢?
A
B
C
A
B
C
图一
图二
在图一中,
∠A
是AB和AC的夹角,
符合图一的条件,它可称为“两边夹角”。
符合图二的条件,
通常
说成“两边和其中一边的对角”
(二)操作交流,初获结论
(第一组完成)
①画一个45°角
②以角的顶点为端点,
在角的两条边上分别
截取2cm、3cm
③得到三角形
④剪下这个三角形
(第二组完成)
①画一个60°角
②以角的顶点为端点,
在角的两条边上分别
截取5cm、6cm
③得到三角形
④剪下这个三角形
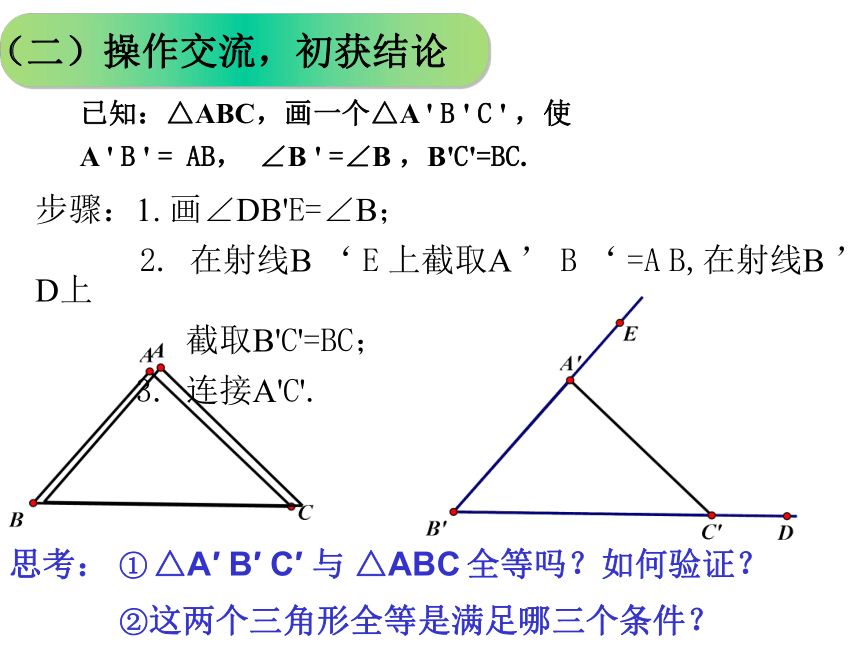
已知:△ABC,画一个△A
'
B
'
C
'
,使
A
'
B
'
=
AB,
∠B
'
=∠B
,B'C'=BC.
(二)操作交流,初获结论
步骤:1.
画∠DB'E=∠B;
2.
在射线B
‘
E
上截取A
’
B
‘
=A
B,在射线B
’
D上
截取B'C'=BC;
3.
连接A'C'.
思考:
①
△A′
B′
C′
与
△ABC
全等吗?如何验证?
②这两个三角形全等是满足哪三个条件?
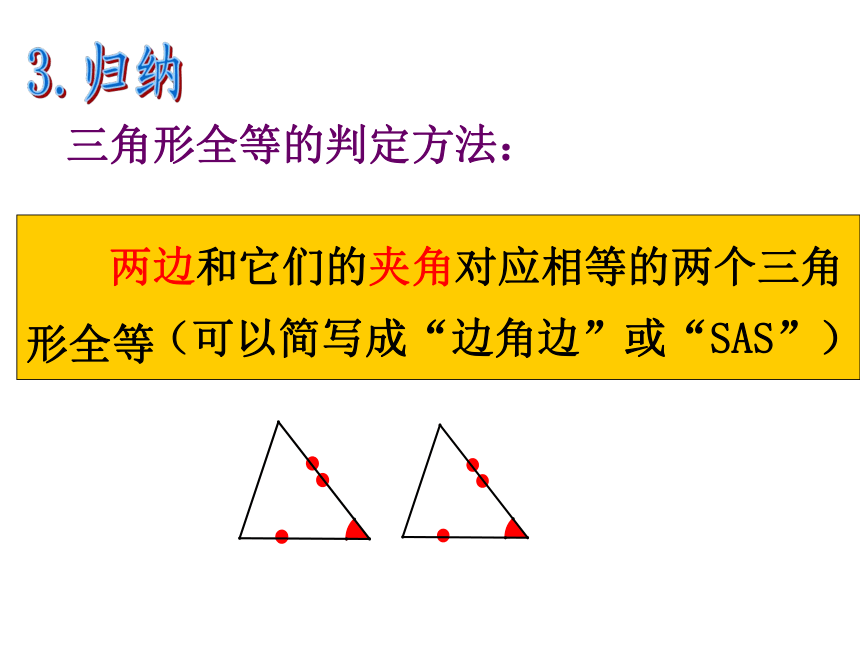
两边和它们的夹角对应相等的两个三角形全等
(可以简写成“边角边”或“SAS”)
三角形全等的判定方法:
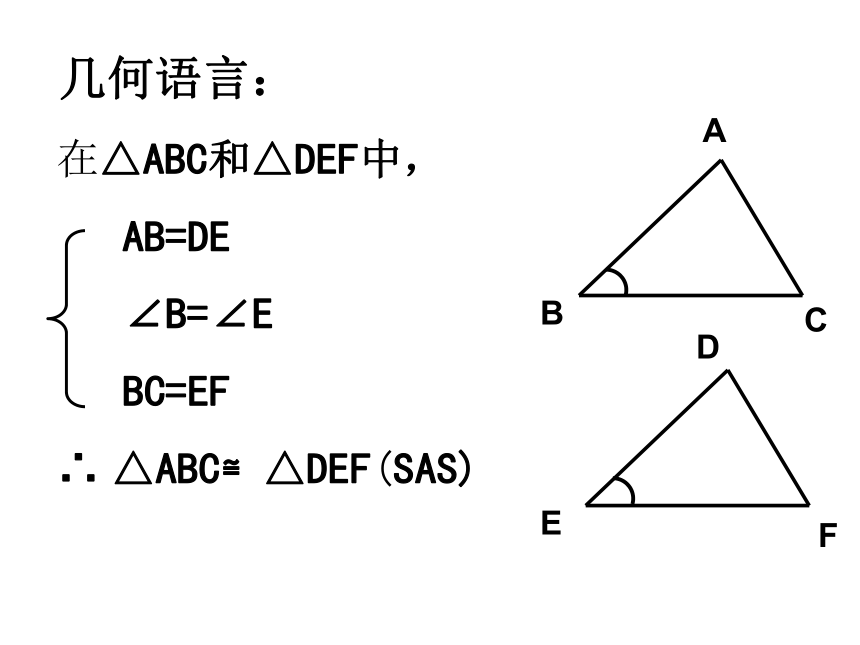
几何语言:
在△ABC和△DEF中,
AB=DE
∠B=∠E
BC=EF
∴
△ABC≌△DEF(SAS)
A
B
C
D
E
F
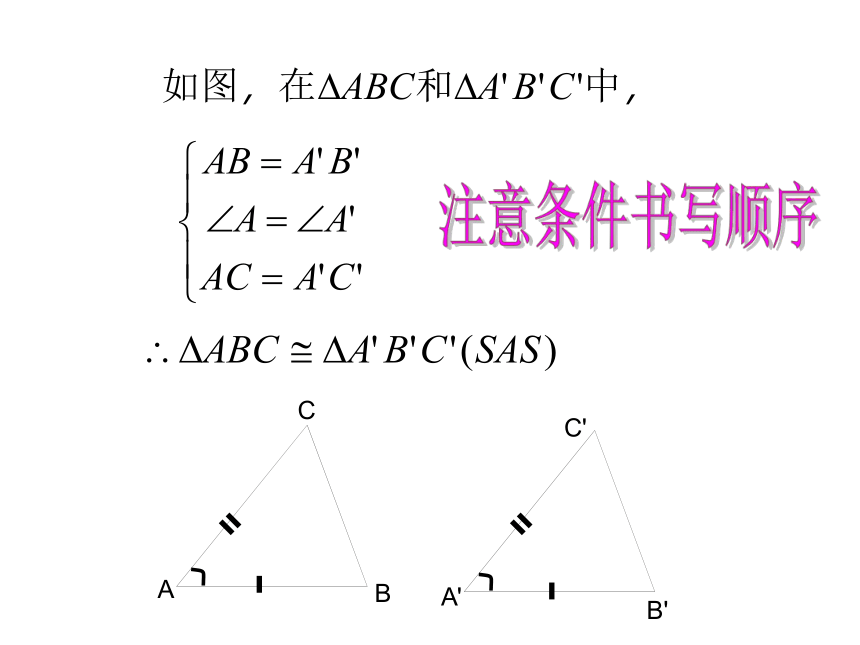
注意条件书写顺序
1.在下列图中找出全等三角形
1
?
30?
8
cm
9
cm
6
?
30?
8
cm
8
cm
Ⅳ
4
8
cm
5
cm
2
30?
?
8
cm
5
cm
5
30?
8
cm
?
5
cm
8
8
cm
5
cm
?
30?
8
cm
9
cm
7
Ⅲ
?
30?
8
cm
8
cm
3
练习一
问题:
有一块三角形的玻璃打碎成如图的两块,如果要到玻璃店去照样配一块,带哪一块去?
C
A
B
D
O
2.在下列推理中填写需要补充的条件,使结论成立:
(1)如图,在△AOB和△DOC中
AO=DO(已知)
______=________(
)
BO=CO(已知)
∴
△AOB≌△DOC(
)
∠
AOB
∠
DOC
对顶角相等
SAS
(2)如图,在△AEC和△ADB中,
AE
=AD
(已知)
_____=
______(
)
AC=
AB
(已知)
∴
△AEC≌△ADB(
)
A
E
B
D
C
SAS
∠A
∠A
公共角
A
E
C
B
D
A
3.已知:
如图,AC=AD,∠CAB=∠DAB.
求证:
BC=BD.
B
A
C
D
证明:在△ACB和△ADB中,
AC=AD
(已知)
∠CAB=∠DAB(已知)
AB=AB(公共边)
∴
△ACB
≌△ADB(SAS)
∴BC=BD(全等三角形的对应边相等)
A
C
B
D
E
A
B
D
C
E
已知:如图BC=EC,CA=CD,∠BCE=∠DCA
求证:
∠B=
∠E
4.若AB=AC,则添加什么条件可得△ABD≌
△ACD?
A
B
D
C
(四)解决问题,深化认识
取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA。连接BC并延长到E,使CE=CB。连接DE,那么量出DE的长就是A,B的距离。
证明:在△ABC和
△DEC中,
CA=CD
∠1=∠2
CB=CE
∴
△ABC≌
△DEC
(SAS)
∴AB=DE
E
1
A
B
C
D
2
●
5.已知:如图,AB=AC,AD=AE.
求证:∠B=∠C
B
A
C
D
E
证明:在△ADB和△AEC中,
AB=AC
(已知)
∠A=∠A(公共角)
AD=AE(已知)
∴
△ADB≌△AEC(SAS)
(全等三角形的对应角相等)
∴
∠B=∠C
B
A
D
C
E
A
以2.5cm,3.5cm为三角形的两边,长度为2.5cm的边所对的角为40°
,情况又怎样?
A
B
C
D
E
F
2.5cm
3.5cm
40°
40°
3.5cm
2.5cm
结论:两边及其一边的对角相等,两个三角形不一定全等
那么由“两边及其中一边的对角对应相等”的条件能判定两个三角形全等吗?为什么?
探究2
1.三角形全等判定2:有两边和它们的______对应相等的两个三角形全等(SAS)
夹角
2.“SAS”的应用中所用到的数学思想:
证明线段(或角相等)
证明线段(或角)所在的两个三角形全等.
转化
七、课堂小结:
祝贺你,在学习中获得了新知识!
作
业:
教科书第43页复习巩固2题
44页10题
全等三角形的判定2
边角边公理
三边对应相等的两个三角形全等(可以简写为“边边边”或“SSS”)。
A
B
C
D
E
F
在△ABC和△
DEF中
∴
△ABC
≌△
DEF(SSS)
AB=DE
BC=EF
CA=FD
用符号语言表达为:
三角形全等判定方法1
知识回顾:
除了SSS外,还有其他情况吗?继续探索三角形全等的条件.
思考
(2)
三条边
(1)
三个角
(3)
两边一角
(4)
两角一边
当两个三角形满足六个条件中的三个时,有四种情况:
SSS
不能!
?
继续探讨三角形全等的条件:
两边一角
思考:已知一个三角形的两条边和一个角,那么这两条边
与这一个角的位置上有几种可能性呢?
A
B
C
A
B
C
图一
图二
在图一中,
∠A
是AB和AC的夹角,
符合图一的条件,它可称为“两边夹角”。
符合图二的条件,
通常
说成“两边和其中一边的对角”
(二)操作交流,初获结论
(第一组完成)
①画一个45°角
②以角的顶点为端点,
在角的两条边上分别
截取2cm、3cm
③得到三角形
④剪下这个三角形
(第二组完成)
①画一个60°角
②以角的顶点为端点,
在角的两条边上分别
截取5cm、6cm
③得到三角形
④剪下这个三角形
已知:△ABC,画一个△A
'
B
'
C
'
,使
A
'
B
'
=
AB,
∠B
'
=∠B
,B'C'=BC.
(二)操作交流,初获结论
步骤:1.
画∠DB'E=∠B;
2.
在射线B
‘
E
上截取A
’
B
‘
=A
B,在射线B
’
D上
截取B'C'=BC;
3.
连接A'C'.
思考:
①
△A′
B′
C′
与
△ABC
全等吗?如何验证?
②这两个三角形全等是满足哪三个条件?
两边和它们的夹角对应相等的两个三角形全等
(可以简写成“边角边”或“SAS”)
三角形全等的判定方法:
几何语言:
在△ABC和△DEF中,
AB=DE
∠B=∠E
BC=EF
∴
△ABC≌△DEF(SAS)
A
B
C
D
E
F
注意条件书写顺序
1.在下列图中找出全等三角形
1
?
30?
8
cm
9
cm
6
?
30?
8
cm
8
cm
Ⅳ
4
8
cm
5
cm
2
30?
?
8
cm
5
cm
5
30?
8
cm
?
5
cm
8
8
cm
5
cm
?
30?
8
cm
9
cm
7
Ⅲ
?
30?
8
cm
8
cm
3
练习一
问题:
有一块三角形的玻璃打碎成如图的两块,如果要到玻璃店去照样配一块,带哪一块去?
C
A
B
D
O
2.在下列推理中填写需要补充的条件,使结论成立:
(1)如图,在△AOB和△DOC中
AO=DO(已知)
______=________(
)
BO=CO(已知)
∴
△AOB≌△DOC(
)
∠
AOB
∠
DOC
对顶角相等
SAS
(2)如图,在△AEC和△ADB中,
AE
=AD
(已知)
_____=
______(
)
AC=
AB
(已知)
∴
△AEC≌△ADB(
)
A
E
B
D
C
SAS
∠A
∠A
公共角
A
E
C
B
D
A
3.已知:
如图,AC=AD,∠CAB=∠DAB.
求证:
BC=BD.
B
A
C
D
证明:在△ACB和△ADB中,
AC=AD
(已知)
∠CAB=∠DAB(已知)
AB=AB(公共边)
∴
△ACB
≌△ADB(SAS)
∴BC=BD(全等三角形的对应边相等)
A
C
B
D
E
A
B
D
C
E
已知:如图BC=EC,CA=CD,∠BCE=∠DCA
求证:
∠B=
∠E
4.若AB=AC,则添加什么条件可得△ABD≌
△ACD?
A
B
D
C
(四)解决问题,深化认识
取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA。连接BC并延长到E,使CE=CB。连接DE,那么量出DE的长就是A,B的距离。
证明:在△ABC和
△DEC中,
CA=CD
∠1=∠2
CB=CE
∴
△ABC≌
△DEC
(SAS)
∴AB=DE
E
1
A
B
C
D
2
●
5.已知:如图,AB=AC,AD=AE.
求证:∠B=∠C
B
A
C
D
E
证明:在△ADB和△AEC中,
AB=AC
(已知)
∠A=∠A(公共角)
AD=AE(已知)
∴
△ADB≌△AEC(SAS)
(全等三角形的对应角相等)
∴
∠B=∠C
B
A
D
C
E
A
以2.5cm,3.5cm为三角形的两边,长度为2.5cm的边所对的角为40°
,情况又怎样?
A
B
C
D
E
F
2.5cm
3.5cm
40°
40°
3.5cm
2.5cm
结论:两边及其一边的对角相等,两个三角形不一定全等
那么由“两边及其中一边的对角对应相等”的条件能判定两个三角形全等吗?为什么?
探究2
1.三角形全等判定2:有两边和它们的______对应相等的两个三角形全等(SAS)
夹角
2.“SAS”的应用中所用到的数学思想:
证明线段(或角相等)
证明线段(或角)所在的两个三角形全等.
转化
七、课堂小结:
祝贺你,在学习中获得了新知识!
作
业:
教科书第43页复习巩固2题
44页10题
