14.2.1 平方差公式 课件-人教版八年级数学上册(共22张ppt)
文档属性
| 名称 | 14.2.1 平方差公式 课件-人教版八年级数学上册(共22张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 370.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-03 21:02:46 | ||
图片预览



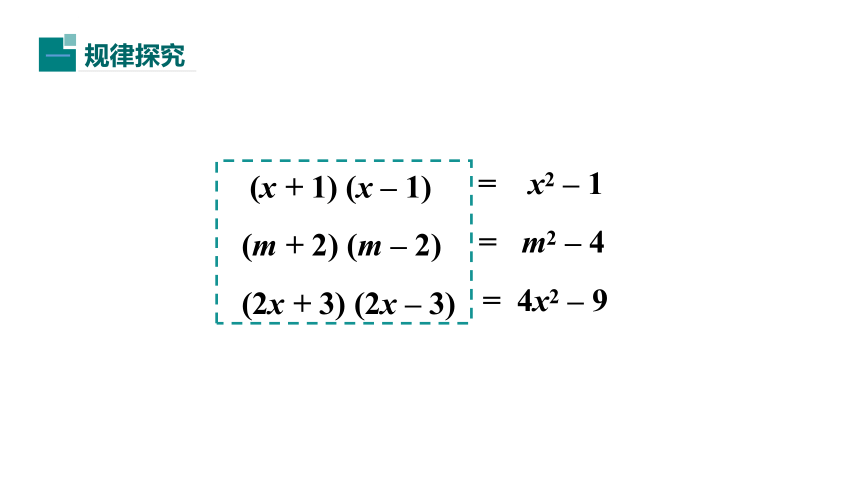
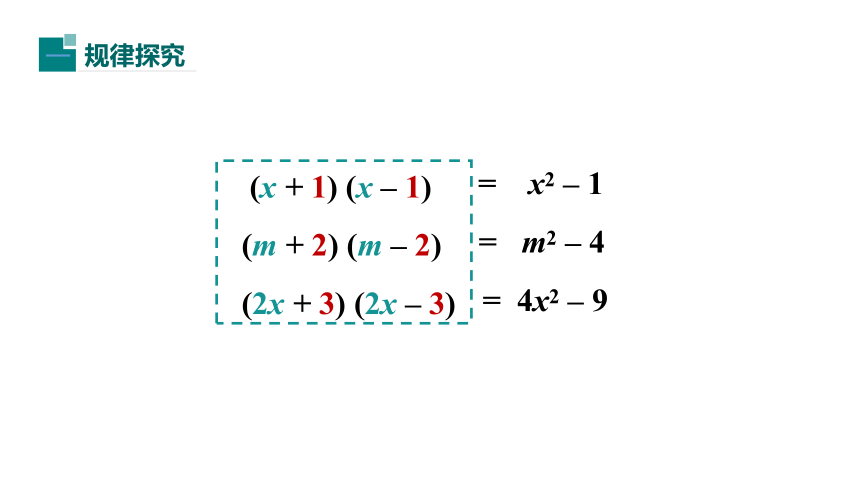
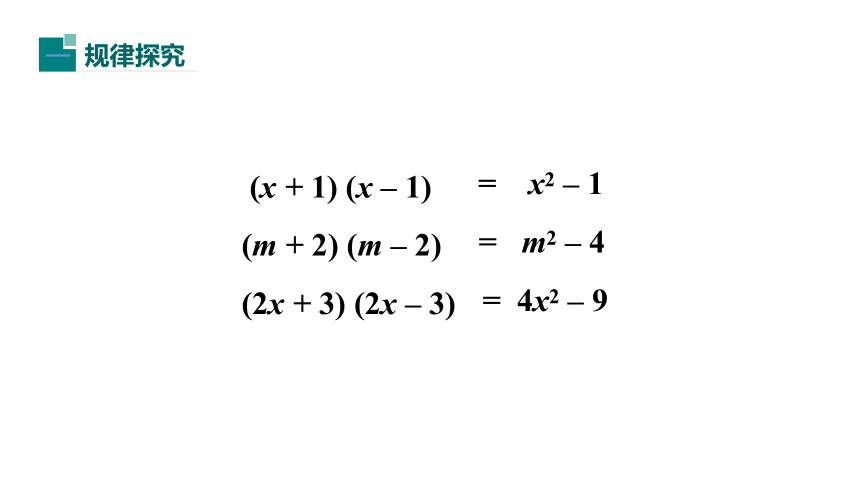
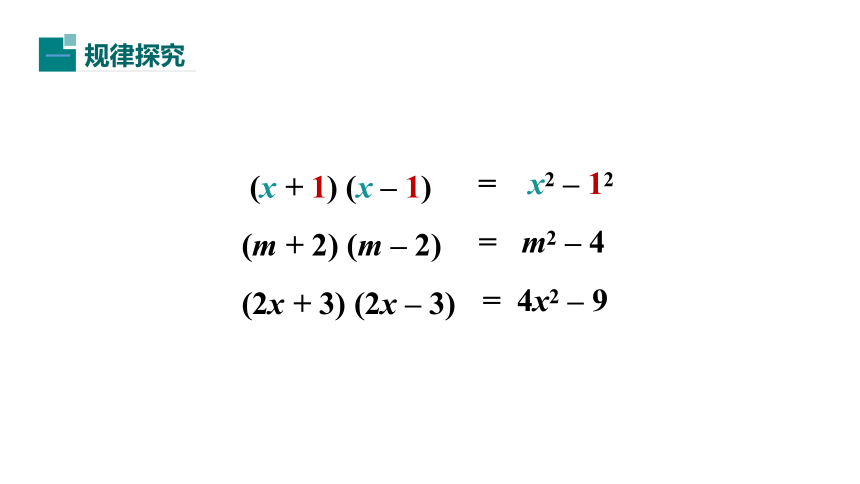
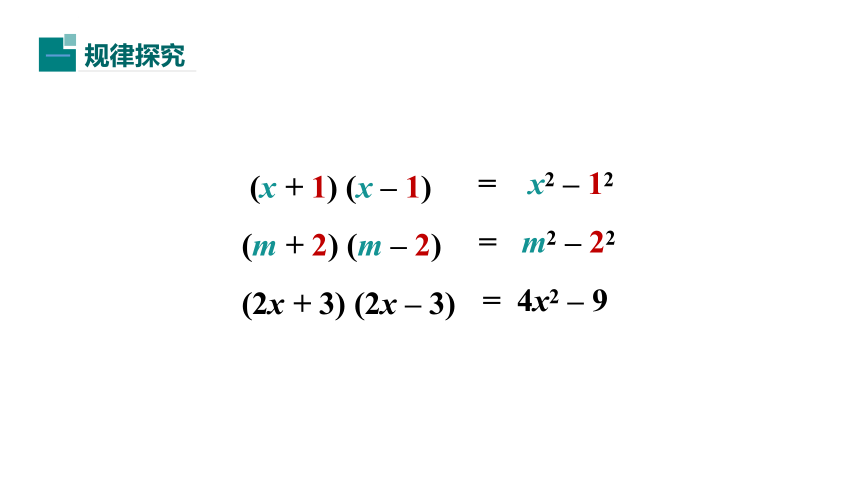
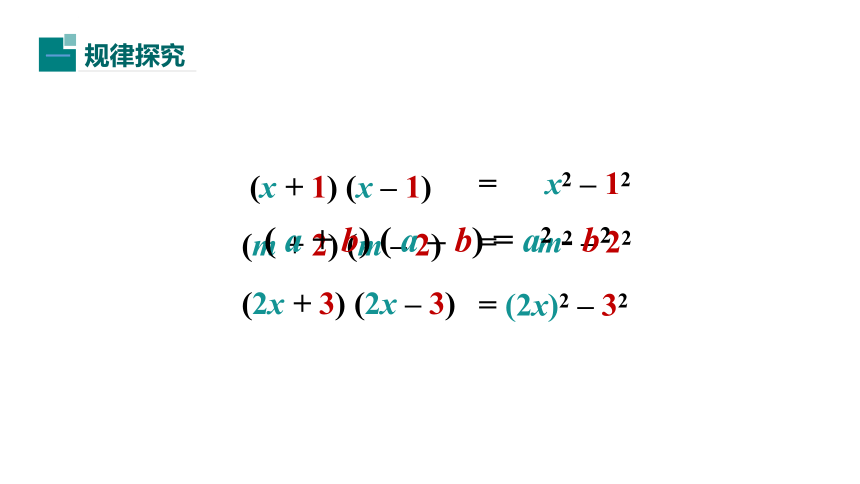
文档简介
(共22张PPT)
14.2
乘法公式
——平方差公式
①
(3x
+
2)
(x
–
2)
②
(2x
+
2)
(2x
–
1)
③
(x
+
1)
(x
–
1)
④
(m
+
2)
(m
–
2)
⑤
(2x
+
3)
(2x
–
3)
请你根据多项式与多项式相乘的法则计算下列多项式的积
=
x2
–
x
+
x
–
1
=
x2
–
1
=
4x2
–
2x
+
4x
–
4
=
4x2
+
2x
–
2
=
3x2
–
6x
+
2x
–
4
=
3x2
–
4x
–
4
=
m2
–
2m
+2m
–
4
=
m2
–
4
=
4x2
–
2x
+
2x
–
9
=
4x2
–
9
规律探究
一
①
(3x
+
2)
(x
–
2)
②
(2x
+
2)
(2x
–
1)
③
(x
+
1)
(x
–
1)
④
(m
+
2)
(m
–
2)
⑤
(2x
+
3)
(2x
–
3)
请你根据多项式与多项式相乘的法则计算下列多项式的积
=
x2
–
x
+
x
–
1
=
x2
–
1
=
4x2
–
2x
+
4x
–
4
=
4x2
+
2x
–
2
=
3x2
–
6x
+
2x
–
4
=
3x2
–
4x
–
4
=
m2
–
2m
+2m
–
4
=
m2
–
4
=
4x2
–
2x
+
2x
–
9
=
4x2
–
9
规律探究
一
(x
+
1)
(x
–
1)
(m
+
2)
(m
–
2)
(2x
+
3)
(2x
–
3)
=
x2
–
1
=
m2
–
4
=
4x2
–
9
规律探究
一
(x
+
1)
(x
–
1)
(m
+
2)
(m
–
2)
(2x
+
3)
(2x
–
3)
=
x2
–
1
=
m2
–
4
=
4x2
–
9
规律探究
一
(x
+
1)
(x
–
1)
(m
+
2)
(m
–
2)
(2x
+
3)
(2x
–
3)
=
x2
–
1
=
m2
–
4
=
4x2
–
9
规律探究
一
(x
+
1)
(x
–
1)
(m
+
2)
(m
–
2)
(2x
+
3)
(2x
–
3)
=
x2
–
12
=
m2
–
4
=
4x2
–
9
规律探究
一
(x
+
1)
(x
–
1)
(m
+
2)
(m
–
2)
(2x
+
3)
(2x
–
3)
=
x2
–
12
=
m2
–
22
=
4x2
–
9
规律探究
一
(x
+
1)
(x
–
1)
(m
+
2)
(m
–
2)
(2x
+
3)
(2x
–
3)
=
x2
–
12
=
m2
–
22
=
(2x)2
–
32
规律探究
一
(
a
+
b)
(
a
–
b)
=
a2
-
b2
两个数的和与这两个数差的积,等于这两个数的平方差.
平方差公式
一
乘法的平方差公式:
(
a
+
b)
(
a
–
b)
=
a2
-
b2
(
a
+
b)
(
b
–
a)
=
a2
-
b2
两个数的和与这两个数差的积,等于这两个数的平方差.
平方差公式
一
乘法的平方差公式:
(
a
+
b)
(
a
–
b)
=
a2
-
b2
(
a
+
b)
(
b
–
a)
=
b2
-
a2
平方差公式——几何证明
一
a
b
b
b
a-b
a-b
(
a
+
b)
(
a
–
b
)
=
a2
-
b2
面积割补的证明方法最早是由我国三国时代的数学家赵爽在注释《周髀算经》说:勾实之矩以股弦差为广,股弦并为袤,而股实方其里。……股实之矩以勾弦差为广,勾弦并为袤,而勾实方其里。
负新余日,聊观《周髀》
赵爽的故事
一
(1+x)(1-x)
(-3+a)(-3-a)
(0.3x-1)(1+0.3x)
(1+a)(-1+a)
a
b
a2-b2
1
x
-3
a
12-x2
(-3)2-a2
a
1
a2-12
0.3x
1
(0.3x)2-12
(a+b)(a-b)
平方差公式——学以致用
一
(a+1)(a-1)
例
1:
(2
+
3x)(
3x
–
2)
(2
+
3x)(-2
–
3x)
(-2
+
3x)(-3x
–
2)
(2
+
3x)(3x
–1)
√
√
×
×
=(3x
+
2)
(3x
–
2)
=(-2
+
3x)
(-2
–
3x)
练习1:下列各式能否利用平方差公式
平方差公式——变式应用
一
①(x
+
2
)(x
–
2
)
=
x2
–
2
练习2:下列各式的计算正确吗?如果不正确,应当怎样改正?
②(-3a
–
2)(3a
–
2
)
=
9a2
–
4
③(4x
+
3y)(4x
–
3y)
=
4x2
–
3y2
④(2xy
–
3)(2xy
+
3)
=
4xy2
–
9
×
×
×
×
=
x2
–
4
=
4
–
9a2
=
16x2
–
9y2
=
4x2y2
–
9
平方差公式——(a+b)(a–b)=a2–b2
一
练习3:
(1)
(3x
+
2
)(
3x
–
2
)
(2)(-x
+
2y)(-x
–
2y)
(
a
+
b
)
(
a
–
b
)
=x2
–
4y2;
解:
(1)
原式=(3x)2
–
22
=
9x2
–
4;
(2)
原式=(-x)2
–
(2y)2
平方差公式——(a+b)(a–b)=a2–b2
一
102×98
例
2:
练习4:
51×49
平方差公式——(a+b)(a–b)=a2–b2
一
解:原式=(100
+
2)(100
–
2)
=1002
–
22
=9996;
原式=(50
+
1)(50
–
1)
=502
–
12
=2499.
例3:
练习5:
(y
+
2)(y
–
2)
–
(y
–
1)
(y
+
5)
(3x
+
4)(3x
–
4)
–
(2x
+
3)(3x
–
2)
平方差公式——(a+b)(a–b)=a2–b2
一
解:例3
原式=
y2
–
22
–
(y2
+
4y
–
5)
=
–
4y
+
1;
练习3
原式=
(3x)2
–
42
–
(6x2
+
5x
–
6)
=
y2
–
4
–
y2
–
4y
+
5
=
9x2
–
16
–
6x2
–
5x
+
6
=
3x2
–
5x
–
10
平方差公式
内容
注意
文字表述:
符号表示:
在应用时,首先观察等号左边的式子是否为两个数的和与差相乘;
对于直观上不符合公式结构特征的,可能经过变形后可以适用;
紧紧抓住
“这两个数”的差来确定
a
和
b
.
课堂小结
一
两个数的和与这两个数差的积,等于这两个数的平方差.
(a+b)(a-b)=a2-b2
习题14.2复习巩固1
作业布置
一
同学们下节课再见
14.2
乘法公式
——平方差公式
①
(3x
+
2)
(x
–
2)
②
(2x
+
2)
(2x
–
1)
③
(x
+
1)
(x
–
1)
④
(m
+
2)
(m
–
2)
⑤
(2x
+
3)
(2x
–
3)
请你根据多项式与多项式相乘的法则计算下列多项式的积
=
x2
–
x
+
x
–
1
=
x2
–
1
=
4x2
–
2x
+
4x
–
4
=
4x2
+
2x
–
2
=
3x2
–
6x
+
2x
–
4
=
3x2
–
4x
–
4
=
m2
–
2m
+2m
–
4
=
m2
–
4
=
4x2
–
2x
+
2x
–
9
=
4x2
–
9
规律探究
一
①
(3x
+
2)
(x
–
2)
②
(2x
+
2)
(2x
–
1)
③
(x
+
1)
(x
–
1)
④
(m
+
2)
(m
–
2)
⑤
(2x
+
3)
(2x
–
3)
请你根据多项式与多项式相乘的法则计算下列多项式的积
=
x2
–
x
+
x
–
1
=
x2
–
1
=
4x2
–
2x
+
4x
–
4
=
4x2
+
2x
–
2
=
3x2
–
6x
+
2x
–
4
=
3x2
–
4x
–
4
=
m2
–
2m
+2m
–
4
=
m2
–
4
=
4x2
–
2x
+
2x
–
9
=
4x2
–
9
规律探究
一
(x
+
1)
(x
–
1)
(m
+
2)
(m
–
2)
(2x
+
3)
(2x
–
3)
=
x2
–
1
=
m2
–
4
=
4x2
–
9
规律探究
一
(x
+
1)
(x
–
1)
(m
+
2)
(m
–
2)
(2x
+
3)
(2x
–
3)
=
x2
–
1
=
m2
–
4
=
4x2
–
9
规律探究
一
(x
+
1)
(x
–
1)
(m
+
2)
(m
–
2)
(2x
+
3)
(2x
–
3)
=
x2
–
1
=
m2
–
4
=
4x2
–
9
规律探究
一
(x
+
1)
(x
–
1)
(m
+
2)
(m
–
2)
(2x
+
3)
(2x
–
3)
=
x2
–
12
=
m2
–
4
=
4x2
–
9
规律探究
一
(x
+
1)
(x
–
1)
(m
+
2)
(m
–
2)
(2x
+
3)
(2x
–
3)
=
x2
–
12
=
m2
–
22
=
4x2
–
9
规律探究
一
(x
+
1)
(x
–
1)
(m
+
2)
(m
–
2)
(2x
+
3)
(2x
–
3)
=
x2
–
12
=
m2
–
22
=
(2x)2
–
32
规律探究
一
(
a
+
b)
(
a
–
b)
=
a2
-
b2
两个数的和与这两个数差的积,等于这两个数的平方差.
平方差公式
一
乘法的平方差公式:
(
a
+
b)
(
a
–
b)
=
a2
-
b2
(
a
+
b)
(
b
–
a)
=
a2
-
b2
两个数的和与这两个数差的积,等于这两个数的平方差.
平方差公式
一
乘法的平方差公式:
(
a
+
b)
(
a
–
b)
=
a2
-
b2
(
a
+
b)
(
b
–
a)
=
b2
-
a2
平方差公式——几何证明
一
a
b
b
b
a-b
a-b
(
a
+
b)
(
a
–
b
)
=
a2
-
b2
面积割补的证明方法最早是由我国三国时代的数学家赵爽在注释《周髀算经》说:勾实之矩以股弦差为广,股弦并为袤,而股实方其里。……股实之矩以勾弦差为广,勾弦并为袤,而勾实方其里。
负新余日,聊观《周髀》
赵爽的故事
一
(1+x)(1-x)
(-3+a)(-3-a)
(0.3x-1)(1+0.3x)
(1+a)(-1+a)
a
b
a2-b2
1
x
-3
a
12-x2
(-3)2-a2
a
1
a2-12
0.3x
1
(0.3x)2-12
(a+b)(a-b)
平方差公式——学以致用
一
(a+1)(a-1)
例
1:
(2
+
3x)(
3x
–
2)
(2
+
3x)(-2
–
3x)
(-2
+
3x)(-3x
–
2)
(2
+
3x)(3x
–1)
√
√
×
×
=(3x
+
2)
(3x
–
2)
=(-2
+
3x)
(-2
–
3x)
练习1:下列各式能否利用平方差公式
平方差公式——变式应用
一
①(x
+
2
)(x
–
2
)
=
x2
–
2
练习2:下列各式的计算正确吗?如果不正确,应当怎样改正?
②(-3a
–
2)(3a
–
2
)
=
9a2
–
4
③(4x
+
3y)(4x
–
3y)
=
4x2
–
3y2
④(2xy
–
3)(2xy
+
3)
=
4xy2
–
9
×
×
×
×
=
x2
–
4
=
4
–
9a2
=
16x2
–
9y2
=
4x2y2
–
9
平方差公式——(a+b)(a–b)=a2–b2
一
练习3:
(1)
(3x
+
2
)(
3x
–
2
)
(2)(-x
+
2y)(-x
–
2y)
(
a
+
b
)
(
a
–
b
)
=x2
–
4y2;
解:
(1)
原式=(3x)2
–
22
=
9x2
–
4;
(2)
原式=(-x)2
–
(2y)2
平方差公式——(a+b)(a–b)=a2–b2
一
102×98
例
2:
练习4:
51×49
平方差公式——(a+b)(a–b)=a2–b2
一
解:原式=(100
+
2)(100
–
2)
=1002
–
22
=9996;
原式=(50
+
1)(50
–
1)
=502
–
12
=2499.
例3:
练习5:
(y
+
2)(y
–
2)
–
(y
–
1)
(y
+
5)
(3x
+
4)(3x
–
4)
–
(2x
+
3)(3x
–
2)
平方差公式——(a+b)(a–b)=a2–b2
一
解:例3
原式=
y2
–
22
–
(y2
+
4y
–
5)
=
–
4y
+
1;
练习3
原式=
(3x)2
–
42
–
(6x2
+
5x
–
6)
=
y2
–
4
–
y2
–
4y
+
5
=
9x2
–
16
–
6x2
–
5x
+
6
=
3x2
–
5x
–
10
平方差公式
内容
注意
文字表述:
符号表示:
在应用时,首先观察等号左边的式子是否为两个数的和与差相乘;
对于直观上不符合公式结构特征的,可能经过变形后可以适用;
紧紧抓住
“这两个数”的差来确定
a
和
b
.
课堂小结
一
两个数的和与这两个数差的积,等于这两个数的平方差.
(a+b)(a-b)=a2-b2
习题14.2复习巩固1
作业布置
一
同学们下节课再见
