高中数学人教A版 必修2第三章3.1.1《直线的倾斜角和斜率》教案
文档属性
| 名称 | 高中数学人教A版 必修2第三章3.1.1《直线的倾斜角和斜率》教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 885.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-03 00:00:00 | ||
图片预览

文档简介
课题
2.1.1倾斜角与斜率
授课年级
高二
课型
新授课
授课时间
主备人
授课教师
教学目标
1.初步了解解析几何的产生及其意义,初步认识坐标法思想2.掌握直线的倾斜角与斜率的概念3.掌握过两点的直线的斜率公式
教学重难点
重点:直线的倾斜角与斜率的概念,过两点的直线斜率公式难点:用直线的倾斜角和斜率刻画直线的几何特征
教学方法
自主探究、合作交流
教学过程
环节设计
学生活动
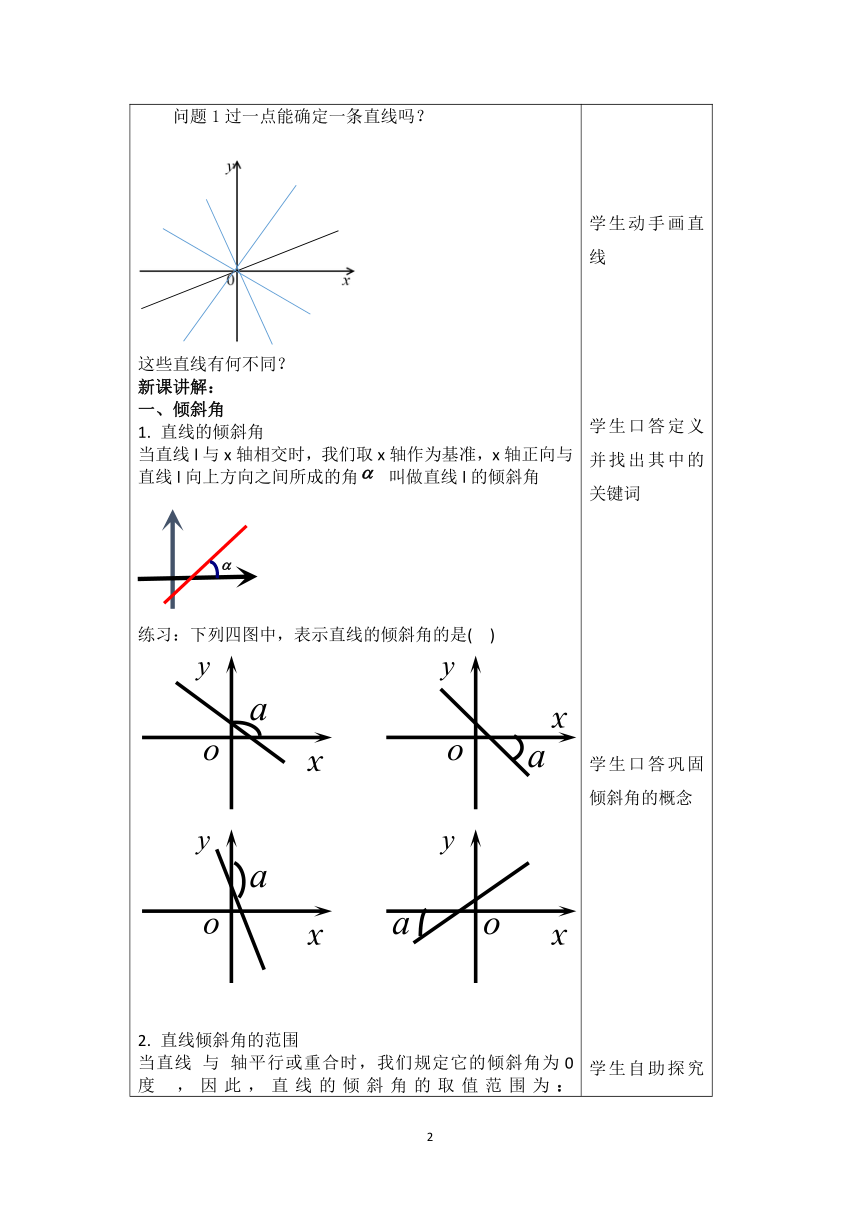
引导语:十六、十七世纪,为了描述现实世界中的运动变化现象,如行星的运动、平面抛体的运动等,需要对它们的运动轨迹进行精确的代数刻画,运动变化进入了数学,变量观念成为数学中的重要理念。在众多数学家工作的基础上,法国数学家笛卡尔、费马集其大成,创立了坐标系,用坐标刻画运动变化。这是解析几何的创始。新课导入:我们知道,点是构成直线的基本元素,在平面直角坐标系中,可以用坐标表示点,本节我们首先在平面直角坐标系中探索确定直线位置的几何要素。引入课题问题1过一点能确定一条直线吗?
这些直线有何不同?新课讲解:一、倾斜角直线的倾斜角当直线l与x轴相交时,我们取x轴作为基准,x轴正向与直线l向上方向之间所成的角叫做直线l的倾斜角练习:下列四图中,表示直线的倾斜角的是(
)直线倾斜角的范围当直线
与
轴平行或重合时,我们规定它的倾斜角为0度
,因此,直线的倾斜角的取值范围为:按倾斜角去分类,直线可分几类?问题2请在平面直角坐标系中,作出倾斜角为
45度
的直线,并对比你与其他同学所作的图像,你发现了什么?若增加条件过点(0,0),你能作多少条直线?3.确定平面直角坐标系中一条直线的几何要素:直线上的一个定点
直线的倾斜角问:日常生活中有没有表示倾斜程度的量?坡度(比)二、直线的斜率直线倾斜角
的正切值,常用小写字母k
表示,即:注意:倾斜角为90度的直线的斜率不存在.探究:借助几何画板,分析直线的倾斜角与斜率的关系。结论:探究:三、过两点的直线的斜率公式思考1.上述公式与两点的顺序有关吗?思考2当直线平行于y轴,或与y轴重合时,上述公式还适用吗?为什么?思考3当直线与x轴平行或重合时,上述公式成立吗?问题3:你能发现直线的方向向量与斜率之间的关系吗?结论:如果直线的一个方向向量为
(x,y),
则它的斜率为___如图,已知A(3,2),B(-4,1),C(0,-1),求直线AB,BC,CA的斜率,并判断这些直线的倾斜角是锐角还是钝角.课堂小结:1.知识点
2.方法过关检测:作业布置教科书习题2.1第1,2,3,4,7.
学生阅读材料了解解析几何的创始学生动手画直线学生口答定义并找出其中的关键词学生口答巩固倾斜角的概念学生自助探究得出倾斜角的范围并指出特殊情况学生相互交流所画直线总结确定直线位置的几何要素借助几何画板学生自主探究倾斜角与斜率的关系学生分小组讨论已知直线上两点坐标求斜率的方法并上台展示通过思考进一步确定公式的使用范围学生总结学生独立完成
板书设计
直线的倾斜角与斜率倾斜角
例题
探究斜率确定直线要素
课堂反思
本节课是解析几何的第一节课,坐标法是本课内容蕴含的核心思想方法,是解析几何研究问题的核心思想方法。通过本节课的学习,学生很好的理解了直线的倾斜角和斜率的概念,理解了倾斜角和斜率是分别从几何和代数两个不同的角度刻画了直线的倾斜程度,教学中紧紧把倾斜角与斜率概念得出重点,在这一过程中让学生积极参与,主动探索,效果良好。不足之处在于已知直线上两点坐标求斜率的探究中不够详细。
y
x
o
l
A
B
C
D
PAGE
4
2.1.1倾斜角与斜率
授课年级
高二
课型
新授课
授课时间
主备人
授课教师
教学目标
1.初步了解解析几何的产生及其意义,初步认识坐标法思想2.掌握直线的倾斜角与斜率的概念3.掌握过两点的直线的斜率公式
教学重难点
重点:直线的倾斜角与斜率的概念,过两点的直线斜率公式难点:用直线的倾斜角和斜率刻画直线的几何特征
教学方法
自主探究、合作交流
教学过程
环节设计
学生活动
引导语:十六、十七世纪,为了描述现实世界中的运动变化现象,如行星的运动、平面抛体的运动等,需要对它们的运动轨迹进行精确的代数刻画,运动变化进入了数学,变量观念成为数学中的重要理念。在众多数学家工作的基础上,法国数学家笛卡尔、费马集其大成,创立了坐标系,用坐标刻画运动变化。这是解析几何的创始。新课导入:我们知道,点是构成直线的基本元素,在平面直角坐标系中,可以用坐标表示点,本节我们首先在平面直角坐标系中探索确定直线位置的几何要素。引入课题问题1过一点能确定一条直线吗?
这些直线有何不同?新课讲解:一、倾斜角直线的倾斜角当直线l与x轴相交时,我们取x轴作为基准,x轴正向与直线l向上方向之间所成的角叫做直线l的倾斜角练习:下列四图中,表示直线的倾斜角的是(
)直线倾斜角的范围当直线
与
轴平行或重合时,我们规定它的倾斜角为0度
,因此,直线的倾斜角的取值范围为:按倾斜角去分类,直线可分几类?问题2请在平面直角坐标系中,作出倾斜角为
45度
的直线,并对比你与其他同学所作的图像,你发现了什么?若增加条件过点(0,0),你能作多少条直线?3.确定平面直角坐标系中一条直线的几何要素:直线上的一个定点
直线的倾斜角问:日常生活中有没有表示倾斜程度的量?坡度(比)二、直线的斜率直线倾斜角
的正切值,常用小写字母k
表示,即:注意:倾斜角为90度的直线的斜率不存在.探究:借助几何画板,分析直线的倾斜角与斜率的关系。结论:探究:三、过两点的直线的斜率公式思考1.上述公式与两点的顺序有关吗?思考2当直线平行于y轴,或与y轴重合时,上述公式还适用吗?为什么?思考3当直线与x轴平行或重合时,上述公式成立吗?问题3:你能发现直线的方向向量与斜率之间的关系吗?结论:如果直线的一个方向向量为
(x,y),
则它的斜率为___如图,已知A(3,2),B(-4,1),C(0,-1),求直线AB,BC,CA的斜率,并判断这些直线的倾斜角是锐角还是钝角.课堂小结:1.知识点
2.方法过关检测:作业布置教科书习题2.1第1,2,3,4,7.
学生阅读材料了解解析几何的创始学生动手画直线学生口答定义并找出其中的关键词学生口答巩固倾斜角的概念学生自助探究得出倾斜角的范围并指出特殊情况学生相互交流所画直线总结确定直线位置的几何要素借助几何画板学生自主探究倾斜角与斜率的关系学生分小组讨论已知直线上两点坐标求斜率的方法并上台展示通过思考进一步确定公式的使用范围学生总结学生独立完成
板书设计
直线的倾斜角与斜率倾斜角
例题
探究斜率确定直线要素
课堂反思
本节课是解析几何的第一节课,坐标法是本课内容蕴含的核心思想方法,是解析几何研究问题的核心思想方法。通过本节课的学习,学生很好的理解了直线的倾斜角和斜率的概念,理解了倾斜角和斜率是分别从几何和代数两个不同的角度刻画了直线的倾斜程度,教学中紧紧把倾斜角与斜率概念得出重点,在这一过程中让学生积极参与,主动探索,效果良好。不足之处在于已知直线上两点坐标求斜率的探究中不够详细。
y
x
o
l
A
B
C
D
PAGE
4
