5.4分式方程(4)分式方程的增根与无解问题-北师大版八年级数学下册课件(共18张PPT)
文档属性
| 名称 | 5.4分式方程(4)分式方程的增根与无解问题-北师大版八年级数学下册课件(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-03 00:00:00 | ||
图片预览





文档简介
北师版八年级下册第五章分式与分式方程 5.4分式方程的增根与无解问题
一:学习目标
1、理解分式方程有增根与无解的意义
2、会根据分式方程有增根或无解确定字母系数的值。
3、会根据分式方程解的符号,求字母系数的取值范围
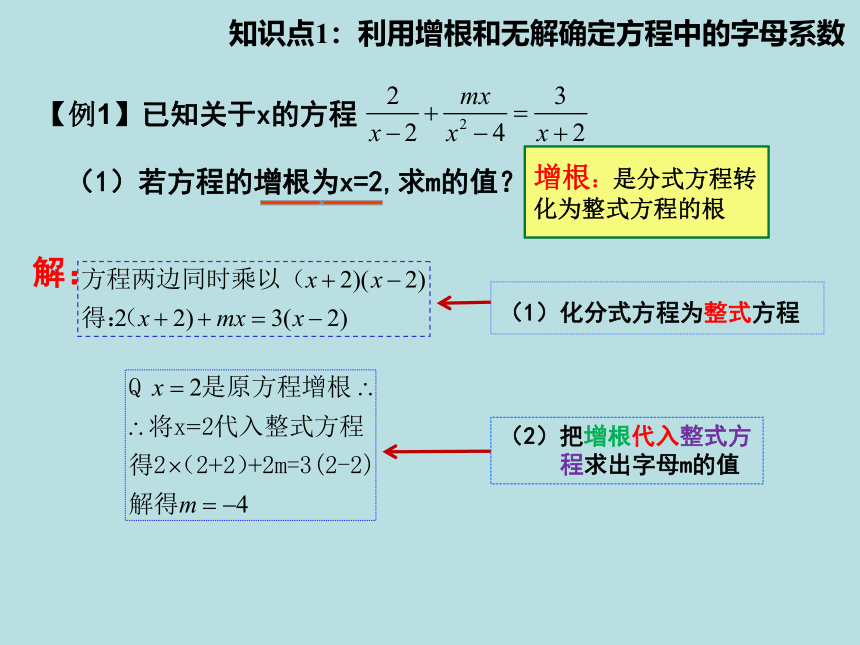
知识点1:利用增根和无解确定方程中的字母系数
【例1】已知关于x的方程
(1)若方程的增根为x=2,求m的值?
解:
增根:是分式方程转化为整式方程的根
(1)化分式方程为整式方程
(2)把增根代入整式方
程求出字母m的值
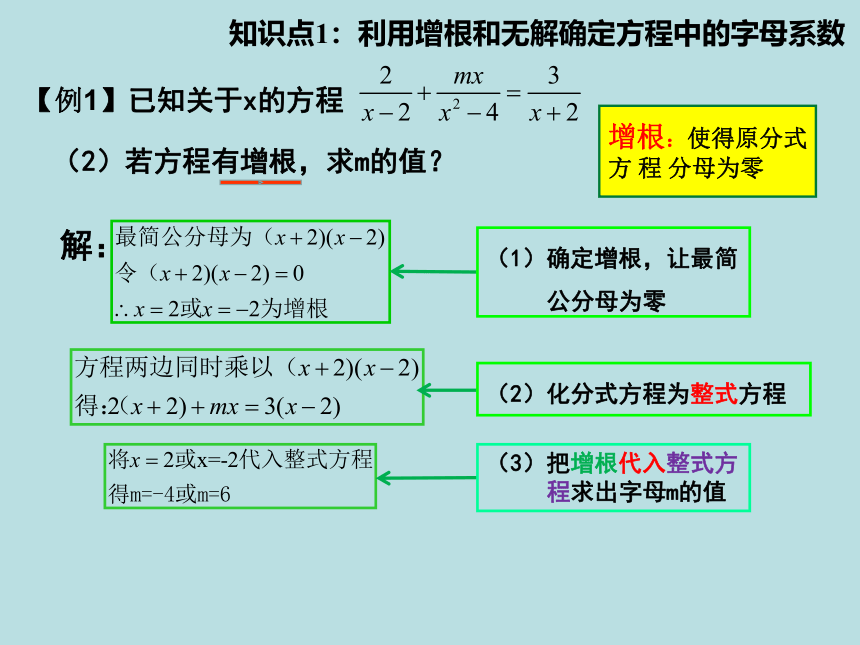
知识点1:利用增根和无解确定方程中的字母系数
【例1】已知关于x的方程
(2)若方程有增根,求m的值?
增根:使得原分式方 程 分母为零
解:
(1)确定增根,让最简
公分母为零
(2)化分式方程为整式方程
(3)把增根代入整式方
程求出字母m的值
解方程:
∴整式方程无解
∴原分式方程无解
引例:分式方程因有增根致使原分式方程无解。那么分式方程无解是否都是由增根造成的?无解和增根一样吗?
1.分式方程无解:
①分式方程有增根
②分式方程转化为整式方程,整式方程无解
2.关于x的方程ax=b,当a=0,b≠0 时,方程无解
归纳小结:
变式:当m为何值时,关于x的方程 无解?
解:
①分式方程有增根:
最简公分母为(x+2)(x-2)
令(x+2)(x-2)=0
∴x=2或x=-2是增根
方程两边同时乘以(x+2)(x-2)
得:2(x+2)+mx=3(x-2)
将x=2或x=-2代入整式方程
得m=-4 或m=6
∴m=-4,m=6分式方程无解
①分式方程有增根
②分式方程转化为整式方程,整式方程
无解:
整理整式方程 2(x+2)+mx=3(x-2)
得:(m-1)x=-10
关于x的方程ax=b,
当a=0,b≠0 时,
方程无解
∴当m-1=0时
∴当m=1时分式方程无解
综上① ②所述,当m=-4,m=6,m=1时原分
式方程无解
即当m=1时整式方程无解
②整式方程无解
方法总结:
1.分式方程无解:
①分式方程有增根
②分式方程转化整式方程,整式方程本身无解
2.步骤
(1)分式方程有增根,求出字母系数的值。
(2)分式方程转化为整式方程,整式方程无解,求出字母系数的值。
(3)综合①②下结论
巩固练习:
1.若关于x的分式方程 无解,则m=
解:
分式方程两边同时乘以x-1得
x+2=- m
令x-1=0 ∴x=1是增根
将x=1代入x+2=-m
得m=-3
-3
①分式方程有增根:
∴当m=-3原分式方程无解
②分式方程转化为整式方程,整式方程
无解:
整理整式方程 x+2==-m
得: x=-m-2
关于x的方程ax=b
当a=1时,整式方程有解
∴整式方程不存在无解的情况
综上① ②所述,当m=-3时原分式方程无解
巩固练习:
2.若分式方程 无解,则m的取值是( )
分式方程两边同时乘以x-1得
2m(x-1)+m+x=0
令 x-1=0 ∴x=1是增根
将x=1代入整式方程得:m=-1
解:
A
①分式方程有增根:
∴当m=-1时分式方程无解
得:(2m+1)x=m
∴当2m+1=0时整式方程无解
②分式方程转化为整式方程,整式方程
无解:
整理整式方程 2m(x-1)+m+x=0
关于x的方程ax=b,
当a=0,b≠0 时,
方程无解
知识点2:已知分式方程解的符号,求字母系数的取值范围
【例2】若分式方程 的解是正数,求a的取值范围?
解:
去分母得:2x+a=-(x-2)
2x+a=-x+2,
2x+x=2-a
3x=2-a,
1.解分式方程,求出x
∴a<2且a≠-4
2.根据题意列不等式组
(注分母不为0)
4.写结论
3.解不等式组
方法总结
X-2≠0
x>0
方法总结:
已知分式方程解的符号
(1)解分式方程,求出x
(2)根据题意列不等式组(注分母不为0)
(3)解不等式组
(4)写结论
知识点2:已知分式方程解的符号,求字母系数的取值范围
若分式方程 的解是负数,则a的取值范围是
解:
去分母得:2x+a=-(x-2)
2x+a=-x+2,
2x+x=2-a
3x=2-a,
∴a>2
例2变式:
a>2
三、课堂小结
四、当堂检测
1、若关于x的方程 有增根,增根是 ,m=
X=3
2
2、关于x的方程 无解,则m的值是( )
A. 0 B. 0或1 C.1 D.2
3.关于x的方程 的解为非正数,求k的取值范围?
解:
B
一:学习目标
1、理解分式方程有增根与无解的意义
2、会根据分式方程有增根或无解确定字母系数的值。
3、会根据分式方程解的符号,求字母系数的取值范围
知识点1:利用增根和无解确定方程中的字母系数
【例1】已知关于x的方程
(1)若方程的增根为x=2,求m的值?
解:
增根:是分式方程转化为整式方程的根
(1)化分式方程为整式方程
(2)把增根代入整式方
程求出字母m的值
知识点1:利用增根和无解确定方程中的字母系数
【例1】已知关于x的方程
(2)若方程有增根,求m的值?
增根:使得原分式方 程 分母为零
解:
(1)确定增根,让最简
公分母为零
(2)化分式方程为整式方程
(3)把增根代入整式方
程求出字母m的值
解方程:
∴整式方程无解
∴原分式方程无解
引例:分式方程因有增根致使原分式方程无解。那么分式方程无解是否都是由增根造成的?无解和增根一样吗?
1.分式方程无解:
①分式方程有增根
②分式方程转化为整式方程,整式方程无解
2.关于x的方程ax=b,当a=0,b≠0 时,方程无解
归纳小结:
变式:当m为何值时,关于x的方程 无解?
解:
①分式方程有增根:
最简公分母为(x+2)(x-2)
令(x+2)(x-2)=0
∴x=2或x=-2是增根
方程两边同时乘以(x+2)(x-2)
得:2(x+2)+mx=3(x-2)
将x=2或x=-2代入整式方程
得m=-4 或m=6
∴m=-4,m=6分式方程无解
①分式方程有增根
②分式方程转化为整式方程,整式方程
无解:
整理整式方程 2(x+2)+mx=3(x-2)
得:(m-1)x=-10
关于x的方程ax=b,
当a=0,b≠0 时,
方程无解
∴当m-1=0时
∴当m=1时分式方程无解
综上① ②所述,当m=-4,m=6,m=1时原分
式方程无解
即当m=1时整式方程无解
②整式方程无解
方法总结:
1.分式方程无解:
①分式方程有增根
②分式方程转化整式方程,整式方程本身无解
2.步骤
(1)分式方程有增根,求出字母系数的值。
(2)分式方程转化为整式方程,整式方程无解,求出字母系数的值。
(3)综合①②下结论
巩固练习:
1.若关于x的分式方程 无解,则m=
解:
分式方程两边同时乘以x-1得
x+2=- m
令x-1=0 ∴x=1是增根
将x=1代入x+2=-m
得m=-3
-3
①分式方程有增根:
∴当m=-3原分式方程无解
②分式方程转化为整式方程,整式方程
无解:
整理整式方程 x+2==-m
得: x=-m-2
关于x的方程ax=b
当a=1时,整式方程有解
∴整式方程不存在无解的情况
综上① ②所述,当m=-3时原分式方程无解
巩固练习:
2.若分式方程 无解,则m的取值是( )
分式方程两边同时乘以x-1得
2m(x-1)+m+x=0
令 x-1=0 ∴x=1是增根
将x=1代入整式方程得:m=-1
解:
A
①分式方程有增根:
∴当m=-1时分式方程无解
得:(2m+1)x=m
∴当2m+1=0时整式方程无解
②分式方程转化为整式方程,整式方程
无解:
整理整式方程 2m(x-1)+m+x=0
关于x的方程ax=b,
当a=0,b≠0 时,
方程无解
知识点2:已知分式方程解的符号,求字母系数的取值范围
【例2】若分式方程 的解是正数,求a的取值范围?
解:
去分母得:2x+a=-(x-2)
2x+a=-x+2,
2x+x=2-a
3x=2-a,
1.解分式方程,求出x
∴a<2且a≠-4
2.根据题意列不等式组
(注分母不为0)
4.写结论
3.解不等式组
方法总结
X-2≠0
x>0
方法总结:
已知分式方程解的符号
(1)解分式方程,求出x
(2)根据题意列不等式组(注分母不为0)
(3)解不等式组
(4)写结论
知识点2:已知分式方程解的符号,求字母系数的取值范围
若分式方程 的解是负数,则a的取值范围是
解:
去分母得:2x+a=-(x-2)
2x+a=-x+2,
2x+x=2-a
3x=2-a,
∴a>2
例2变式:
a>2
三、课堂小结
四、当堂检测
1、若关于x的方程 有增根,增根是 ,m=
X=3
2
2、关于x的方程 无解,则m的值是( )
A. 0 B. 0或1 C.1 D.2
3.关于x的方程 的解为非正数,求k的取值范围?
解:
B
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
