北师大版八年级下册5.3分式的加减(2)课件(共21张PPT)
文档属性
| 名称 | 北师大版八年级下册5.3分式的加减(2)课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-03 13:34:47 | ||
图片预览








文档简介
5.3分式的加减法(2)
北师大版 初中数学 八年级下册 第五章
学习目标
1.经历探索异分母的分式加减运算法则的过程,培养代数化归意识,发展合情推理能力.
2.掌握异分母的分式加减法的法则,会通分,能进行简单分式的加减运算,发展运算能力.
3.能解决一些与分式加减有关的简单的实际问题,体会分式的模型思想.
一、复习回顾
1.分式的基本性质:
分式的分子和分母同时乘(或除以)同一个不为零的整式,分式的值不变.
2.同分母分式的加减法法则:
同分母的分式相加减,分母不变,把分子相加减.
一、复习回顾
3.计算:
解:
二、探究新知1
如何计算:
依据?
转化
根据分数的基本性质,异分母分数转化为同分母分数,这一过程称为通分.
通分
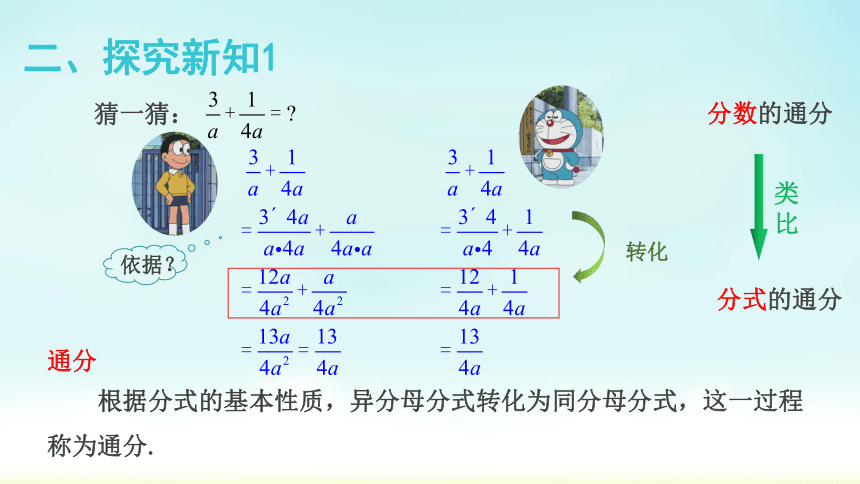
二、探究新知1
猜一猜:
根据分式的基本性质,异分母分式转化为同分母分式,这一过程称为通分.
通分
依据?
转化
分数的通分
分式的通分
类比
二、探究新知2
谁的公分母更简单?
二、探究新知2
如何找最简公分母?
1.系数:最小公倍数;
2.相同字母:最高次幂;
3.单独的字母及其指数.
二、探究新知2
如何找最简公分母?
多项式先分解因式
乘胜追击:给下列各式通分.
二、探究新知2
依据?
二、探究新知3
异分母分数的加减法法则:
异分母的分数相加减,先通分,化为同分母的分数,然后再按同分母分数的加减法法则进行计算.
异分母的分式相加减,先通分,化为同分母的分式,然后再按同分母分式的加减法法则进行计算.
异分母分数的加减法法则:
类比
二、探究新知3
异分母分数的加减法法则:
异分母的分式相加减,先通分,化为同分母的分式,然后再按同分母分式的加减法法则进行计算.
文字语言:
数学语言:
a,b,c,d可以表示什么?
三、典例分析
例1.计算:
先通分
异分母的分式相加减,先通分,化为同分母的分式,然后再按同分母分式的加减法法则进行计算.
解:
化最简
三、典例分析
分母是多项式,先因式分解.
异分母的分式相加减,先通分,化为同分母的分式,然后再按同分母分式的加减法法则进行计算.
三、典例分析
例2.小刚家和小丽家到学校的路程都是3km,其中小丽走的是平路,骑车速度2vkm/h.小刚需要走1km的上坡路、2km的下坡路,在上坡路上的骑车速度为vkm/h,在下坡路上的骑车速度为3vkm/h.那么:
(1)小刚从家到学校需要多长时间?
(2)小刚和小丽谁在路上花费的时间少?少用多长时间?
小刚从家到学校需要:
小丽从家到学校需要:
三、典例分析
(2)小刚和小丽谁在路上花费的时间少?少用多长时间?
小刚从家到学校需要:
小丽从家到学校需要:
小丽在路上花费的时间少.
小丽比小刚在路上花费时间少:
怎么比较?
四、随堂练习
1.将下列各分式通分:
2.计算:
四、随堂练习
解:
四、随堂练习
解:
五、课堂小结
同分母分式的加减法
1.确定最简公分母;
转化
异分母分式的加减法
3.分子相加减,分母不变;
2.通分;
4.化最简.
六、课后作业
北师大版 初中数学 八年级下册 第五章
学习目标
1.经历探索异分母的分式加减运算法则的过程,培养代数化归意识,发展合情推理能力.
2.掌握异分母的分式加减法的法则,会通分,能进行简单分式的加减运算,发展运算能力.
3.能解决一些与分式加减有关的简单的实际问题,体会分式的模型思想.
一、复习回顾
1.分式的基本性质:
分式的分子和分母同时乘(或除以)同一个不为零的整式,分式的值不变.
2.同分母分式的加减法法则:
同分母的分式相加减,分母不变,把分子相加减.
一、复习回顾
3.计算:
解:
二、探究新知1
如何计算:
依据?
转化
根据分数的基本性质,异分母分数转化为同分母分数,这一过程称为通分.
通分
二、探究新知1
猜一猜:
根据分式的基本性质,异分母分式转化为同分母分式,这一过程称为通分.
通分
依据?
转化
分数的通分
分式的通分
类比
二、探究新知2
谁的公分母更简单?
二、探究新知2
如何找最简公分母?
1.系数:最小公倍数;
2.相同字母:最高次幂;
3.单独的字母及其指数.
二、探究新知2
如何找最简公分母?
多项式先分解因式
乘胜追击:给下列各式通分.
二、探究新知2
依据?
二、探究新知3
异分母分数的加减法法则:
异分母的分数相加减,先通分,化为同分母的分数,然后再按同分母分数的加减法法则进行计算.
异分母的分式相加减,先通分,化为同分母的分式,然后再按同分母分式的加减法法则进行计算.
异分母分数的加减法法则:
类比
二、探究新知3
异分母分数的加减法法则:
异分母的分式相加减,先通分,化为同分母的分式,然后再按同分母分式的加减法法则进行计算.
文字语言:
数学语言:
a,b,c,d可以表示什么?
三、典例分析
例1.计算:
先通分
异分母的分式相加减,先通分,化为同分母的分式,然后再按同分母分式的加减法法则进行计算.
解:
化最简
三、典例分析
分母是多项式,先因式分解.
异分母的分式相加减,先通分,化为同分母的分式,然后再按同分母分式的加减法法则进行计算.
三、典例分析
例2.小刚家和小丽家到学校的路程都是3km,其中小丽走的是平路,骑车速度2vkm/h.小刚需要走1km的上坡路、2km的下坡路,在上坡路上的骑车速度为vkm/h,在下坡路上的骑车速度为3vkm/h.那么:
(1)小刚从家到学校需要多长时间?
(2)小刚和小丽谁在路上花费的时间少?少用多长时间?
小刚从家到学校需要:
小丽从家到学校需要:
三、典例分析
(2)小刚和小丽谁在路上花费的时间少?少用多长时间?
小刚从家到学校需要:
小丽从家到学校需要:
小丽在路上花费的时间少.
小丽比小刚在路上花费时间少:
怎么比较?
四、随堂练习
1.将下列各分式通分:
2.计算:
四、随堂练习
解:
四、随堂练习
解:
五、课堂小结
同分母分式的加减法
1.确定最简公分母;
转化
异分母分式的加减法
3.分子相加减,分母不变;
2.通分;
4.化最简.
六、课后作业
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
