北师大版八年级下册第三章图形的平移与旋转单元复习课件( 25张PPT)
文档属性
| 名称 | 北师大版八年级下册第三章图形的平移与旋转单元复习课件( 25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-03 13:37:09 | ||
图片预览



文档简介
八年级下册数学北师大版
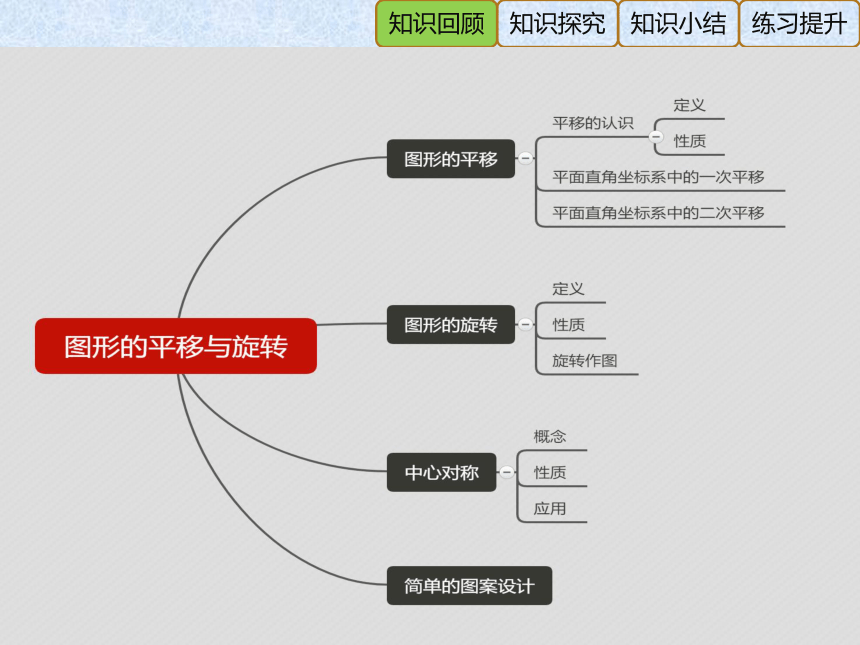
第三章 图形的平移与旋转
单元复习
知识回顾
知识探究
练习提升
知识小结
知识回顾
知识探究
练习提升
知识小结
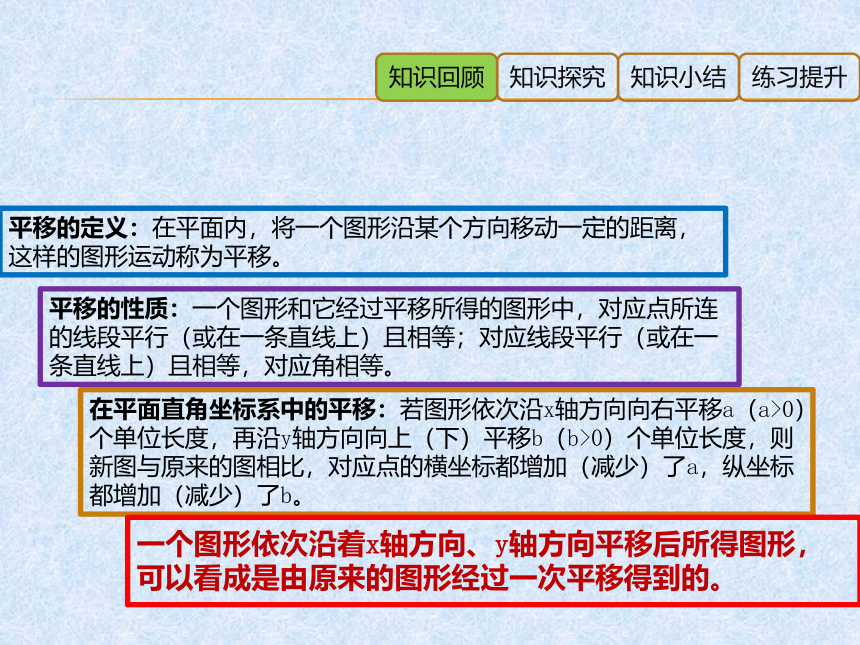
平移的定义:在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移。
平移的性质:一个图形和它经过平移所得的图形中,对应点所连的线段平行(或在一条直线上)且相等;对应线段平行(或在一条直线上)且相等,对应角相等。
在平面直角坐标系中的平移:若图形依次沿x轴方向向右平移a(a>0)个单位长度,再沿y轴方向向上(下)平移b(b>0)个单位长度,则新图与原来的图相比,对应点的横坐标都增加(减少)了a,纵坐标都增加(减少)了b。
一个图形依次沿着x轴方向、y轴方向平移后所得图形,可以看成是由原来的图形经过一次平移得到的。
知识回顾
知识探究
练习提升
知识小结
旋转的定义:
在平面内,将一个图形绕一个定点 按某个方向转动一个角度,这样的图形运动称为旋转,这个定点称为旋转中心,转动的角称为旋转角。
旋转的性质:
一个图形和它经过旋转所得的图形中,对应点到旋转中心的距离相等,任意一组对应点与旋转中心的连线所成的角都等于旋转角;对应线段相等,对应角相等。
旋转作图的三要素:旋转中心、旋转方向和旋转角度.
中心对称图形:把一个图形绕某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形,这个点叫做它的对称中心。
中心对称:如果把一个图形绕着某一点旋转180°,它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做它们的对称中心。
知识回顾
知识探究
练习提升
知识小结
知识回顾
知识探究
练习提升
知识小结
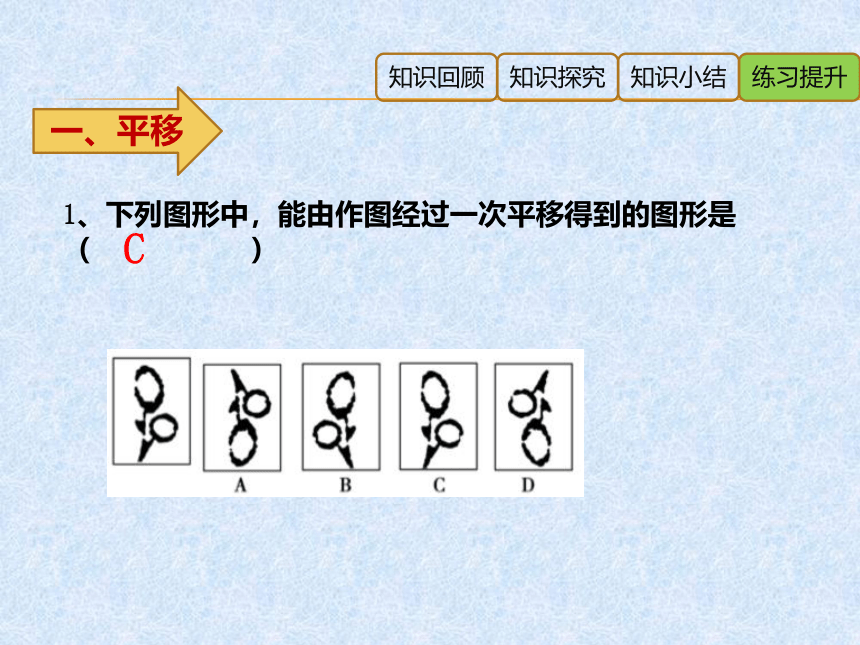
1、下列图形中,能由作图经过一次平移得到的图形是( )
C
一、平移
知识回顾
知识探究
练习提升
知识小结
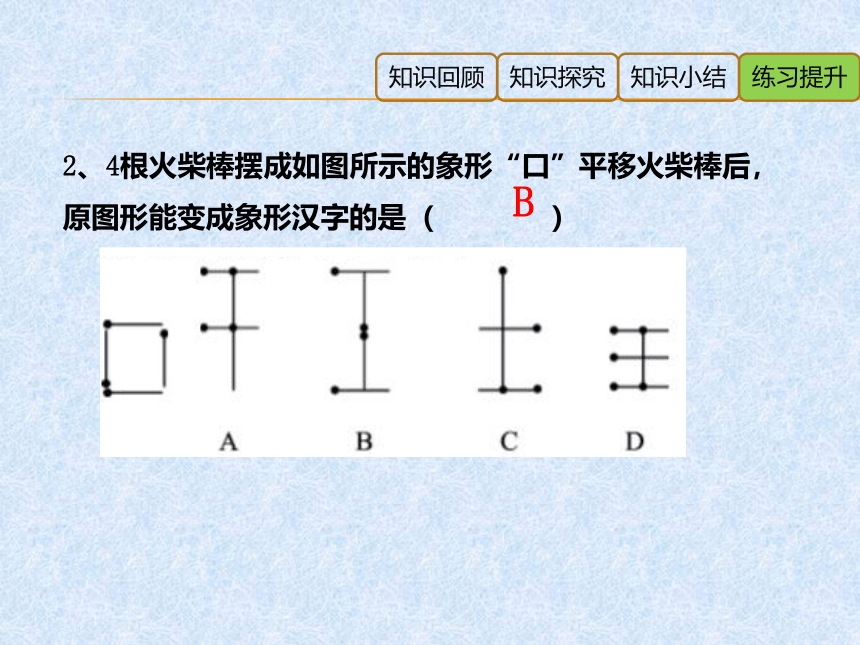
2、4根火柴棒摆成如图所示的象形“口”平移火柴棒后,原图形能变成象形汉字的是( )
B
知识回顾
知识探究
练习提升
知识小结
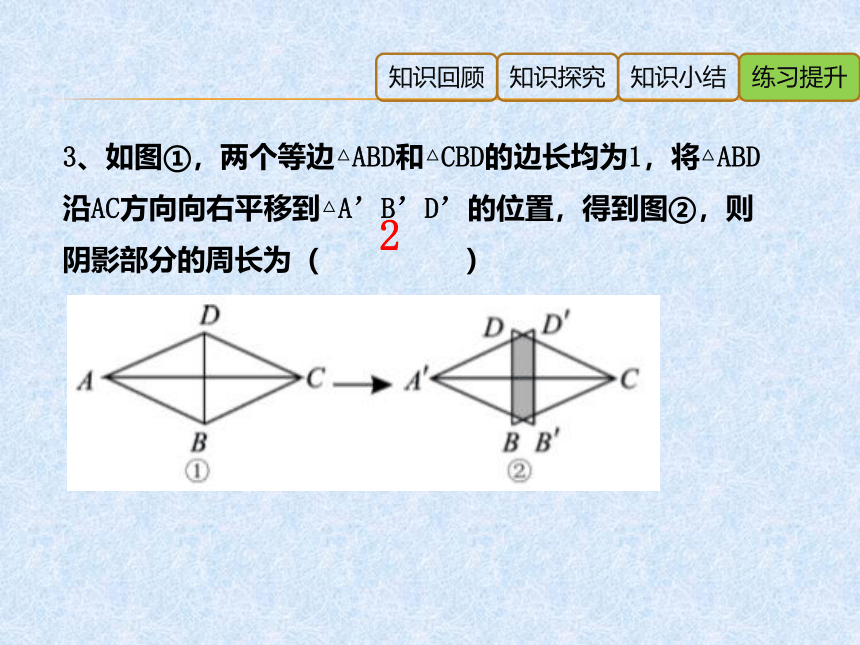
3、如图①,两个等边△ABD和△CBD的边长均为1,将△ABD沿AC方向向右平移到△A’B’D’的位置,得到图②,则阴影部分的周长为( )
2
知识回顾
知识探究
练习提升
知识小结
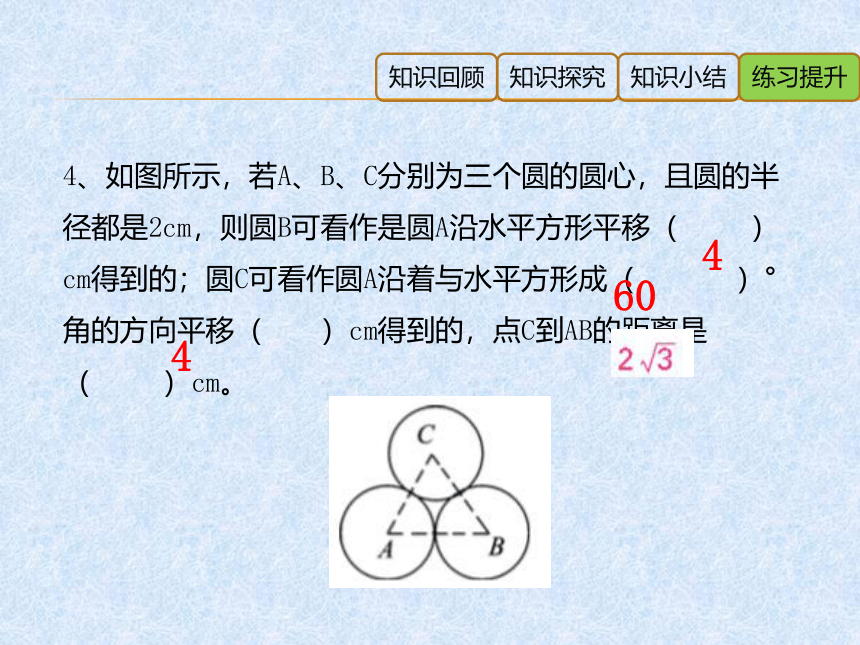
4、如图所示,若A、B、C分别为三个圆的圆心,且圆的半径都是2cm,则圆B可看作是圆A沿水平方形平移( )cm得到的;圆C可看作圆A沿着与水平方形成( )°角的方向平移( )cm得到的,点C到AB的距离是( )cm。
4
60
4
知识回顾
知识探究
练习提升
知识小结
二、旋转
5、下列几种运动,只属于旋转的有( )
(1)直升机起飞后螺旋桨的运动
(2)发电机的风车运动
(3)在笔直轨道上运行的列车
(4)传送带上的机器零件
A 0种 B 1种 C 2种 D 3种
B
平移加旋转
知识回顾
知识探究
练习提升
知识小结
6、如图所示的图案有如下说法,其中正确的有( )
(1)该图形是轴对称图形
(2)该图形是中心对称图形
(3)该图形既是轴对称图形,又是中心对称图形
(4)该图形绕中心旋转60°后,能与原图形重合
A 4种 B 1种 C 2种 D 3种
A
知识回顾
知识探究
练习提升
知识小结
7、如图,该图围绕自己的旋转中心按下列角度旋转后,不能与其自身重合的是( )
A.72° B.108° C.144° D.216°
B
知识回顾
知识探究
练习提升
知识小结
8、如图,已知△ABC三个顶点的坐标分别为A(0,4)B(-1,1)C(-2,2)。将△ABC向右平移4个单位长度,得到△A’B’C’,点A,B,C的对应点分别为A’,B’,C’,再将△ A’B’C’绕点B’顺时针旋转90°,得到△A’’B’’C’’,点A’,B’,C’的对应点分别为A’’、B’’、C’’,则点A’’的坐标为( )
6,0
知识回顾
知识探究
练习提升
知识小结
9.下列电视台的台标,是中心对称图形的是( )
三、中心对称
D
知识回顾
知识探究
练习提升
知识小结
10.考考你的眼力,下列四张扑克牌中是中心对称图形的是( )
C
知识回顾
知识探究
练习提升
知识小结
四、综合运用
11.已知△ABC在平面直角坐标系中的位置如图所示。
(1)分别写出图中点A和点C的坐标;
(2)画出△ABC绕点C顺时针方向旋转90°后的△A’B’C’。
(3)求点A旋转到点A’所经过的路线长度(结果保留π)。
知识回顾
知识探究
练习提升
知识小结
解:(1)A(0,4)C(3,1)
(2)如图所示
(3)由勾股定理得:AC=3 2,点A旋转到 A’所经过的路线长为?×2π×3 2=
√
√
知识回顾
知识探究
练习提升
知识小结
12.如图,在平面直角坐标系中,△ABC的各个定点坐标是A(-2,3)、B(-4,-1)、C(2,0),点P(m,n)为△ABC内的一点,△ABC平移后得到△A’B’C’,点P平移到P’(m+6,n+1)处。
(1)直接写出点A’B’C’的坐标;
(2)作出平移后的图形;
(3)若点M(-3,b)为边AB上的点,则对应点M’的坐标是什么?
(4)如果将△A’B’C’看成是由△ABC经过一次平移得到的,请指出这一平移的方向和平移的距离。
知识回顾
知识探究
练习提升
知识小结
解:(1)A’(4,4)B’(2,0) C’(8,1)
(2)图形如图所示
(3)M’(3,b+1)
(4)
平移的方向是由B到C(或B’)的方向,平移的距离是√37个单位。
知识回顾
知识探究
练习提升
知识小结
13.如图,四边形ABCD是正方形,E、F分别是DC和CB延长线上的点,且DE=BF,连接AE,AF,EF.
(1)求证:△ADE≌△ABF
(2)填空:△ABF可以由△ADE绕旋转中心( )点 ,按顺时针方向旋转( )得到。
(3)若BC=8,DE=6,求△AEF的面积。
知识回顾
知识探究
练习提升
知识小结
(1)证明:∵四边形ABCD是正方形
∴AD=AB,∠D=∠ABC=90°,而F是CB的延长线上的点
∴∠ABF=∠D=90°
又∵AB=AD, DE=BF
∴ △ADE≌△ABF
(2)A 90°
(3)解:∵BC=8
∴AD=8,在Rt△ADE中,DE=6, AD8
∴AE= √AD2+DE2=10
∵△ABF可以由△ADE绕旋转中心A点,按顺时针方向旋转90°得到
∴AE=AF, ∠EAF=90°
∴△AEF的面积=?AE2=?×100=50
知识回顾
知识探究
练习提升
知识小结
知识回顾
知识探究
练习提升
知识小结
14.将两块大小相同的含30°角的直角三角板(∠BAC=∠B1A1C=30)按图①的方式放置,固定三角板B1A1C,然后将三角板ABC绕直角顶点C顺时针方向旋转(旋转角小于90°)至图②所示的位置,AB与A1C交于点E,AC与B1A1交于点F,AB与B1A1交于点O。
知识回顾
知识探究
练习提升
知识小结
(1)求证:△BCE≌△ B1 CF;
(2)当旋转角等于30°时,AB与B1A1垂直吗?请说明理由。
知识回顾
知识探究
练习提升
知识小结
(1)证明:∵在△BEC和△B1 CF中,∠B=∠B1=60°,BC=B1 C,∠BCE=90°-∠A1CA=∠B1 CF
∴△BCE≌ △B1 CF(ASA)
(2)解: 当∠ A1CA=30°时,AB⊥A1B1
理由:∵ ∠ A1CA=30°
∴∠ B1 CF=90°-30°=60°
∴∠B1 FC=180°-∠B1 CF-∠B1=180°-60°-60°=60°
∴∠AFO=∠B1 FC=60°
∵∠A=30°
∴∠AOF=180°-∠A-∠AFO=180°-30°-60°=90°
∴ AB⊥A1B1
第三章 图形的平移与旋转
单元复习
知识回顾
知识探究
练习提升
知识小结
知识回顾
知识探究
练习提升
知识小结
平移的定义:在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移。
平移的性质:一个图形和它经过平移所得的图形中,对应点所连的线段平行(或在一条直线上)且相等;对应线段平行(或在一条直线上)且相等,对应角相等。
在平面直角坐标系中的平移:若图形依次沿x轴方向向右平移a(a>0)个单位长度,再沿y轴方向向上(下)平移b(b>0)个单位长度,则新图与原来的图相比,对应点的横坐标都增加(减少)了a,纵坐标都增加(减少)了b。
一个图形依次沿着x轴方向、y轴方向平移后所得图形,可以看成是由原来的图形经过一次平移得到的。
知识回顾
知识探究
练习提升
知识小结
旋转的定义:
在平面内,将一个图形绕一个定点 按某个方向转动一个角度,这样的图形运动称为旋转,这个定点称为旋转中心,转动的角称为旋转角。
旋转的性质:
一个图形和它经过旋转所得的图形中,对应点到旋转中心的距离相等,任意一组对应点与旋转中心的连线所成的角都等于旋转角;对应线段相等,对应角相等。
旋转作图的三要素:旋转中心、旋转方向和旋转角度.
中心对称图形:把一个图形绕某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形,这个点叫做它的对称中心。
中心对称:如果把一个图形绕着某一点旋转180°,它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做它们的对称中心。
知识回顾
知识探究
练习提升
知识小结
知识回顾
知识探究
练习提升
知识小结
1、下列图形中,能由作图经过一次平移得到的图形是( )
C
一、平移
知识回顾
知识探究
练习提升
知识小结
2、4根火柴棒摆成如图所示的象形“口”平移火柴棒后,原图形能变成象形汉字的是( )
B
知识回顾
知识探究
练习提升
知识小结
3、如图①,两个等边△ABD和△CBD的边长均为1,将△ABD沿AC方向向右平移到△A’B’D’的位置,得到图②,则阴影部分的周长为( )
2
知识回顾
知识探究
练习提升
知识小结
4、如图所示,若A、B、C分别为三个圆的圆心,且圆的半径都是2cm,则圆B可看作是圆A沿水平方形平移( )cm得到的;圆C可看作圆A沿着与水平方形成( )°角的方向平移( )cm得到的,点C到AB的距离是( )cm。
4
60
4
知识回顾
知识探究
练习提升
知识小结
二、旋转
5、下列几种运动,只属于旋转的有( )
(1)直升机起飞后螺旋桨的运动
(2)发电机的风车运动
(3)在笔直轨道上运行的列车
(4)传送带上的机器零件
A 0种 B 1种 C 2种 D 3种
B
平移加旋转
知识回顾
知识探究
练习提升
知识小结
6、如图所示的图案有如下说法,其中正确的有( )
(1)该图形是轴对称图形
(2)该图形是中心对称图形
(3)该图形既是轴对称图形,又是中心对称图形
(4)该图形绕中心旋转60°后,能与原图形重合
A 4种 B 1种 C 2种 D 3种
A
知识回顾
知识探究
练习提升
知识小结
7、如图,该图围绕自己的旋转中心按下列角度旋转后,不能与其自身重合的是( )
A.72° B.108° C.144° D.216°
B
知识回顾
知识探究
练习提升
知识小结
8、如图,已知△ABC三个顶点的坐标分别为A(0,4)B(-1,1)C(-2,2)。将△ABC向右平移4个单位长度,得到△A’B’C’,点A,B,C的对应点分别为A’,B’,C’,再将△ A’B’C’绕点B’顺时针旋转90°,得到△A’’B’’C’’,点A’,B’,C’的对应点分别为A’’、B’’、C’’,则点A’’的坐标为( )
6,0
知识回顾
知识探究
练习提升
知识小结
9.下列电视台的台标,是中心对称图形的是( )
三、中心对称
D
知识回顾
知识探究
练习提升
知识小结
10.考考你的眼力,下列四张扑克牌中是中心对称图形的是( )
C
知识回顾
知识探究
练习提升
知识小结
四、综合运用
11.已知△ABC在平面直角坐标系中的位置如图所示。
(1)分别写出图中点A和点C的坐标;
(2)画出△ABC绕点C顺时针方向旋转90°后的△A’B’C’。
(3)求点A旋转到点A’所经过的路线长度(结果保留π)。
知识回顾
知识探究
练习提升
知识小结
解:(1)A(0,4)C(3,1)
(2)如图所示
(3)由勾股定理得:AC=3 2,点A旋转到 A’所经过的路线长为?×2π×3 2=
√
√
知识回顾
知识探究
练习提升
知识小结
12.如图,在平面直角坐标系中,△ABC的各个定点坐标是A(-2,3)、B(-4,-1)、C(2,0),点P(m,n)为△ABC内的一点,△ABC平移后得到△A’B’C’,点P平移到P’(m+6,n+1)处。
(1)直接写出点A’B’C’的坐标;
(2)作出平移后的图形;
(3)若点M(-3,b)为边AB上的点,则对应点M’的坐标是什么?
(4)如果将△A’B’C’看成是由△ABC经过一次平移得到的,请指出这一平移的方向和平移的距离。
知识回顾
知识探究
练习提升
知识小结
解:(1)A’(4,4)B’(2,0) C’(8,1)
(2)图形如图所示
(3)M’(3,b+1)
(4)
平移的方向是由B到C(或B’)的方向,平移的距离是√37个单位。
知识回顾
知识探究
练习提升
知识小结
13.如图,四边形ABCD是正方形,E、F分别是DC和CB延长线上的点,且DE=BF,连接AE,AF,EF.
(1)求证:△ADE≌△ABF
(2)填空:△ABF可以由△ADE绕旋转中心( )点 ,按顺时针方向旋转( )得到。
(3)若BC=8,DE=6,求△AEF的面积。
知识回顾
知识探究
练习提升
知识小结
(1)证明:∵四边形ABCD是正方形
∴AD=AB,∠D=∠ABC=90°,而F是CB的延长线上的点
∴∠ABF=∠D=90°
又∵AB=AD, DE=BF
∴ △ADE≌△ABF
(2)A 90°
(3)解:∵BC=8
∴AD=8,在Rt△ADE中,DE=6, AD8
∴AE= √AD2+DE2=10
∵△ABF可以由△ADE绕旋转中心A点,按顺时针方向旋转90°得到
∴AE=AF, ∠EAF=90°
∴△AEF的面积=?AE2=?×100=50
知识回顾
知识探究
练习提升
知识小结
知识回顾
知识探究
练习提升
知识小结
14.将两块大小相同的含30°角的直角三角板(∠BAC=∠B1A1C=30)按图①的方式放置,固定三角板B1A1C,然后将三角板ABC绕直角顶点C顺时针方向旋转(旋转角小于90°)至图②所示的位置,AB与A1C交于点E,AC与B1A1交于点F,AB与B1A1交于点O。
知识回顾
知识探究
练习提升
知识小结
(1)求证:△BCE≌△ B1 CF;
(2)当旋转角等于30°时,AB与B1A1垂直吗?请说明理由。
知识回顾
知识探究
练习提升
知识小结
(1)证明:∵在△BEC和△B1 CF中,∠B=∠B1=60°,BC=B1 C,∠BCE=90°-∠A1CA=∠B1 CF
∴△BCE≌ △B1 CF(ASA)
(2)解: 当∠ A1CA=30°时,AB⊥A1B1
理由:∵ ∠ A1CA=30°
∴∠ B1 CF=90°-30°=60°
∴∠B1 FC=180°-∠B1 CF-∠B1=180°-60°-60°=60°
∴∠AFO=∠B1 FC=60°
∵∠A=30°
∴∠AOF=180°-∠A-∠AFO=180°-30°-60°=90°
∴ AB⊥A1B1
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
