北师大版八年级下册数学 6.3三角形的中位线课件(共20张PPT)
文档属性
| 名称 | 北师大版八年级下册数学 6.3三角形的中位线课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 286.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-03 00:00:00 | ||
图片预览







文档简介
A
B
C
在三角形中,连结一个顶点和它的对边中点的线段叫做 三角形的中线。
顶点
顶点
D
中点
DE称三 角形的做什么呢?
E
中点
它就是我们这节课要学习的三角形的中位线。
复习引入
1
§6.3三角形的中位线
自主学习
2
阅读教材151页,解决相应问题并思考下列问题:
1、三角形的中位线与底边有什么位置关系?
2、三角形的中位线与底边有什么数量关系?
3、你能说出教材证明三角形中位线定理的思路吗?这和小明解决分割问题有什么相似之处?
你还有其他的证明方法吗?
C
A
B
D
E
三角形中位线的性质定理
三角形的中位线平行于第三边,并且等于它的一半。
C
A
B
D
E
用符号语言表示
∵DE是△ABC的中位线
∴ DE∥BC,
DE= BC.
2
1
数量关系
位置关系
点拨归纳
3
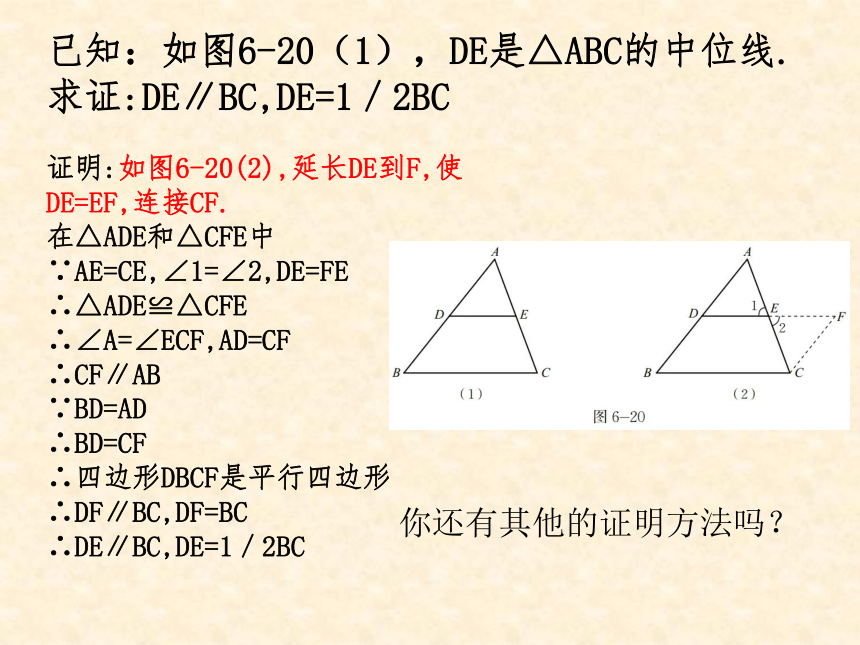
已知:如图6-20(1),DE是△ABC的中位线.
求证:DE∥BC,DE=1/2BC
证明:如图6-20(2),延长DE到F,使
DE=EF,连接CF.
在△ADE和△CFE中
∵AE=CE,∠1=∠2,DE=FE
∴△ADE≌△CFE
∴∠A=∠ECF,AD=CF
∴CF∥AB
∵BD=AD
∴BD=CF
∴四边形DBCF是平行四边形
∴DF∥BC,DF=BC
∴DE∥BC,DE=1/2BC
你还有其他的证明方法吗?
C
E
D
F
B
A
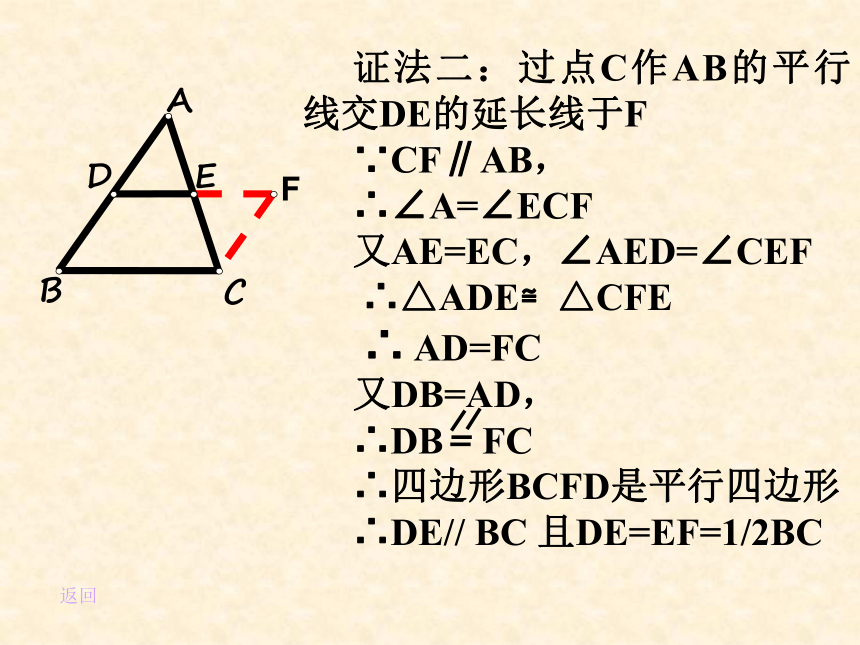
证法二:过点C作AB的平行线交DE的延长线于F
∵CF∥AB,
∴∠A=∠ECF
又AE=EC,∠AED=∠CEF
∴△ADE≌△CFE
∴ AD=FC
又DB=AD,
∴DB FC
∴四边形BCFD是平行四边形
∴DE// BC 且DE=EF=1/2BC
返回
A
B
C
E
D
F
证法三:如图,延长DE至F,
使EF=DE,
连接CD、AF、CF
∵AE=EC
∴DE=EF
∴四边形ADCF是平行四边形∴AD FC
又D为AB中点,
∴DB FC
∴四边形BCFD是平行四边形?
∴DE// BC 且DE=EF=1/2BC
返回
A
C
E
D
F
G
B
证法四:如图,过E作AB的平行线交BC于F,自A作BC的平行线交FE于G
∵AG∥BC∴∠EAG=∠ECF
又∵ AE=EC, ∠AEG=∠CEF
∴△AEG≌△CEF∴AG=FC,GE=EF
又AB∥GF,AG∥BF∴四边形ABFG是平行四边形
∴BF=AG=FC,AB=GF
又D为AB中点,E为GF中点,
∴DB EF
∴四边形DBFE是平行四边形
∴DE∥BF,即DE∥BC,DE=BF=FC
即DE=1/2BC
返回
A
C
B
E
D
F
1、如图,在△ABC中,D、E、F分别是AB、AC、BC的中点:
①若∠ADE=65°,则∠B= 度。
②若BC=8cm,则DE= cm。
65
4
③若AC=4cm,BC=6cm,AB=8cm,
则△DEF的周长=______
9cm
④若△ABC的周长为24,△DEF的周长是_____
12
⑤若△ABC的面积为24,△DEF的面积是_____
6
自检互评
4
A
C
A1
B1
C1
B
小三角形的周长等于△ABC周长的一半;
小三角形的面积等于△ABC面积的1/4。
2、思考:(1)三角形三条中位线围成的三角形和原三角形的周长有什么联系?
(2)三角形三条中位线围成的三角形和原三角形的面积有什么联系?
1、任意画一个△ABC,作出它的所有中位线。
A
C
A1
B1
C1
B
①图中有几个平行四边形?
三个平行四边形
②这几条中位线把三角形分
割成几个全等的小三角形?
四个全等三角形
③这些小三角形的周长
(面积)与△ABC的周长
(面积)有怎样的关系?
小三角形的周长等于△ABC周长的一半;
小三角形的面积等于△ABC面积的1/4。
如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.
猜想四边形EFGH的形状并证明。
A
B
C
D
E
F
G
H
E,F是AB,BC的中点,你联想到什么?
要使EF成为一个三角形的中位线应怎样添加辅助线?
证明:如图,连接AC
∵EF是△ABC的中位线
同理得:
∴四边形EFGH是平行四边形
答: 四边形EFGH为平行四边形。
典例分析
4
变式1.若四边形ABCD从普通形状变成平行四边形,其它条件不变,则四边形EFGH的形状会变化吗?为什么?
A
B
C
D
E
F
G
H
变式2.若四边形ABCD从普通的四边形变成矩形,其它条件不变,则四边形EFGH的形状会变化吗?为什么?
B
A
C
D
E
F
G
H
变式3.若四边形ABCD从普通的四边形变成菱形,其它条件不变,则四边形EFGH的形状会有变化吗?为什么?
A
B
C
D
E
F
G
H
变式4.若四边形ABCD从普通四边形变成正方形,其它的条件不变,则四边形EFGH的形状会有变化吗?为什么?
A
B
C
D
E
F
G
H
拓展延伸
5
1、如图,O是△ABC内一点,连接OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连接 ,如果 DEFG能构成四边形。(1)当O在△ABC内时,四边形DEFG是平行四边形吗?说明理由;
(2)当点O移到△ABC外时,(1) 的结论是否成立?画出图形并说明理由。
O
G
F
E
C
D
B
A
2、已知△ABC中,AD是中线,点E在AD上,AE=ED,连接CE并延长交AB于点F,请猜想AF与BF之间有什么数量关系?并说明理由。
H
E
F
D
C
B
A
3、如图所示,已知第一个三角形的周长为1,它的三条中位线组成第二个三角形,第二个三角形的中位线又组成第三个三角形,以此类推,第2017个三角形的周长是多少?
课堂小结
6
1、三角形中线与中位线的区别。
2、三角形中位线定理有两个结论:
(1)表示位置关系------平行于第三边;
(2)表示数量关系------等于第三边的一半。
应用时要具体分析,需要哪一个就用哪一个。
B
C
在三角形中,连结一个顶点和它的对边中点的线段叫做 三角形的中线。
顶点
顶点
D
中点
DE称三 角形的做什么呢?
E
中点
它就是我们这节课要学习的三角形的中位线。
复习引入
1
§6.3三角形的中位线
自主学习
2
阅读教材151页,解决相应问题并思考下列问题:
1、三角形的中位线与底边有什么位置关系?
2、三角形的中位线与底边有什么数量关系?
3、你能说出教材证明三角形中位线定理的思路吗?这和小明解决分割问题有什么相似之处?
你还有其他的证明方法吗?
C
A
B
D
E
三角形中位线的性质定理
三角形的中位线平行于第三边,并且等于它的一半。
C
A
B
D
E
用符号语言表示
∵DE是△ABC的中位线
∴ DE∥BC,
DE= BC.
2
1
数量关系
位置关系
点拨归纳
3
已知:如图6-20(1),DE是△ABC的中位线.
求证:DE∥BC,DE=1/2BC
证明:如图6-20(2),延长DE到F,使
DE=EF,连接CF.
在△ADE和△CFE中
∵AE=CE,∠1=∠2,DE=FE
∴△ADE≌△CFE
∴∠A=∠ECF,AD=CF
∴CF∥AB
∵BD=AD
∴BD=CF
∴四边形DBCF是平行四边形
∴DF∥BC,DF=BC
∴DE∥BC,DE=1/2BC
你还有其他的证明方法吗?
C
E
D
F
B
A
证法二:过点C作AB的平行线交DE的延长线于F
∵CF∥AB,
∴∠A=∠ECF
又AE=EC,∠AED=∠CEF
∴△ADE≌△CFE
∴ AD=FC
又DB=AD,
∴DB FC
∴四边形BCFD是平行四边形
∴DE// BC 且DE=EF=1/2BC
返回
A
B
C
E
D
F
证法三:如图,延长DE至F,
使EF=DE,
连接CD、AF、CF
∵AE=EC
∴DE=EF
∴四边形ADCF是平行四边形∴AD FC
又D为AB中点,
∴DB FC
∴四边形BCFD是平行四边形?
∴DE// BC 且DE=EF=1/2BC
返回
A
C
E
D
F
G
B
证法四:如图,过E作AB的平行线交BC于F,自A作BC的平行线交FE于G
∵AG∥BC∴∠EAG=∠ECF
又∵ AE=EC, ∠AEG=∠CEF
∴△AEG≌△CEF∴AG=FC,GE=EF
又AB∥GF,AG∥BF∴四边形ABFG是平行四边形
∴BF=AG=FC,AB=GF
又D为AB中点,E为GF中点,
∴DB EF
∴四边形DBFE是平行四边形
∴DE∥BF,即DE∥BC,DE=BF=FC
即DE=1/2BC
返回
A
C
B
E
D
F
1、如图,在△ABC中,D、E、F分别是AB、AC、BC的中点:
①若∠ADE=65°,则∠B= 度。
②若BC=8cm,则DE= cm。
65
4
③若AC=4cm,BC=6cm,AB=8cm,
则△DEF的周长=______
9cm
④若△ABC的周长为24,△DEF的周长是_____
12
⑤若△ABC的面积为24,△DEF的面积是_____
6
自检互评
4
A
C
A1
B1
C1
B
小三角形的周长等于△ABC周长的一半;
小三角形的面积等于△ABC面积的1/4。
2、思考:(1)三角形三条中位线围成的三角形和原三角形的周长有什么联系?
(2)三角形三条中位线围成的三角形和原三角形的面积有什么联系?
1、任意画一个△ABC,作出它的所有中位线。
A
C
A1
B1
C1
B
①图中有几个平行四边形?
三个平行四边形
②这几条中位线把三角形分
割成几个全等的小三角形?
四个全等三角形
③这些小三角形的周长
(面积)与△ABC的周长
(面积)有怎样的关系?
小三角形的周长等于△ABC周长的一半;
小三角形的面积等于△ABC面积的1/4。
如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.
猜想四边形EFGH的形状并证明。
A
B
C
D
E
F
G
H
E,F是AB,BC的中点,你联想到什么?
要使EF成为一个三角形的中位线应怎样添加辅助线?
证明:如图,连接AC
∵EF是△ABC的中位线
同理得:
∴四边形EFGH是平行四边形
答: 四边形EFGH为平行四边形。
典例分析
4
变式1.若四边形ABCD从普通形状变成平行四边形,其它条件不变,则四边形EFGH的形状会变化吗?为什么?
A
B
C
D
E
F
G
H
变式2.若四边形ABCD从普通的四边形变成矩形,其它条件不变,则四边形EFGH的形状会变化吗?为什么?
B
A
C
D
E
F
G
H
变式3.若四边形ABCD从普通的四边形变成菱形,其它条件不变,则四边形EFGH的形状会有变化吗?为什么?
A
B
C
D
E
F
G
H
变式4.若四边形ABCD从普通四边形变成正方形,其它的条件不变,则四边形EFGH的形状会有变化吗?为什么?
A
B
C
D
E
F
G
H
拓展延伸
5
1、如图,O是△ABC内一点,连接OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连接 ,如果 DEFG能构成四边形。(1)当O在△ABC内时,四边形DEFG是平行四边形吗?说明理由;
(2)当点O移到△ABC外时,(1) 的结论是否成立?画出图形并说明理由。
O
G
F
E
C
D
B
A
2、已知△ABC中,AD是中线,点E在AD上,AE=ED,连接CE并延长交AB于点F,请猜想AF与BF之间有什么数量关系?并说明理由。
H
E
F
D
C
B
A
3、如图所示,已知第一个三角形的周长为1,它的三条中位线组成第二个三角形,第二个三角形的中位线又组成第三个三角形,以此类推,第2017个三角形的周长是多少?
课堂小结
6
1、三角形中线与中位线的区别。
2、三角形中位线定理有两个结论:
(1)表示位置关系------平行于第三边;
(2)表示数量关系------等于第三边的一半。
应用时要具体分析,需要哪一个就用哪一个。
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
