北师大版八年级下册数学:6·4 多边形的外角和 课件(共24张PPT)
文档属性
| 名称 | 北师大版八年级下册数学:6·4 多边形的外角和 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-03 00:00:00 | ||
图片预览





文档简介
平行四边形
第 六 章
6·4 多边形的外角和
第二课时
北师大版八年级数学下册
目 录
CONTENTS
1
2
3
4
创设情境 激发兴趣
温故知新 理解概念
合作探究 感悟新知
探究归纳 课堂小结
01
创设情境 激发兴趣
看一看
02
温故知新 理解概念
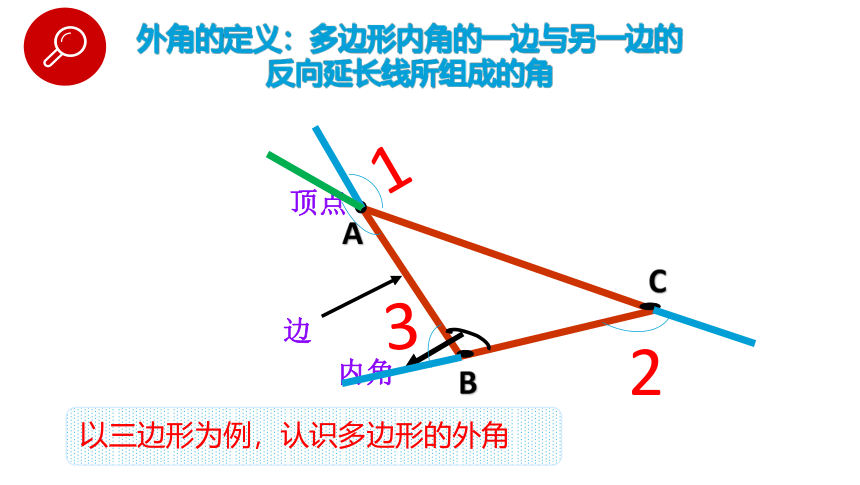
外角的定义:多边形内角的一边与另一边的反向延长线所组成的角
顶点
内角
边
A
B
C
以三边形为例,认识多边形的外角
1
2
3
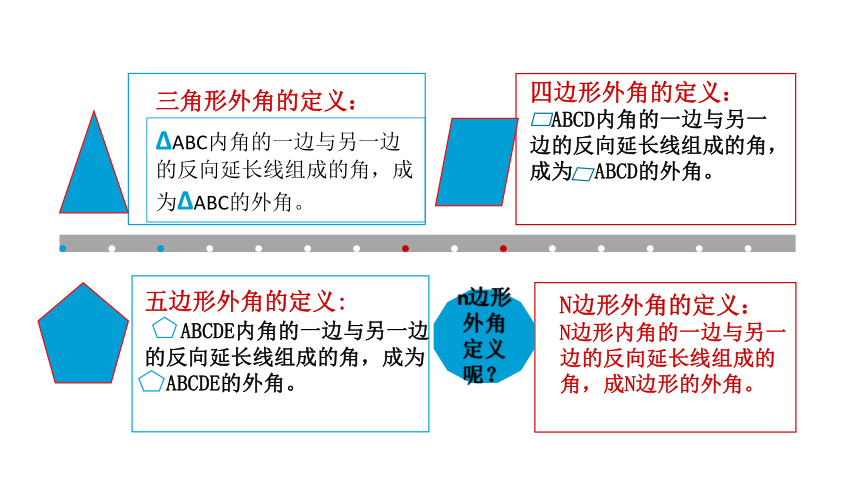
三角形外角的定义:
四边形外角的定义:
ABCD内角的一边与另一边的反向延长线组成的角,成为 ABCD的外角。
五边形外角的定义:
ABCDE内角的一边与另一边的反向延长线组成的角,成为
ABCDE的外角。
N边形外角的定义:
N边形内角的一边与另一边的反向延长线组成的角,成N边形的外角。
n边形外角定义呢?
?ABC内角的一边与另一边的反向延长线组成的角,成为?ABC的外角。
1
2
3
4
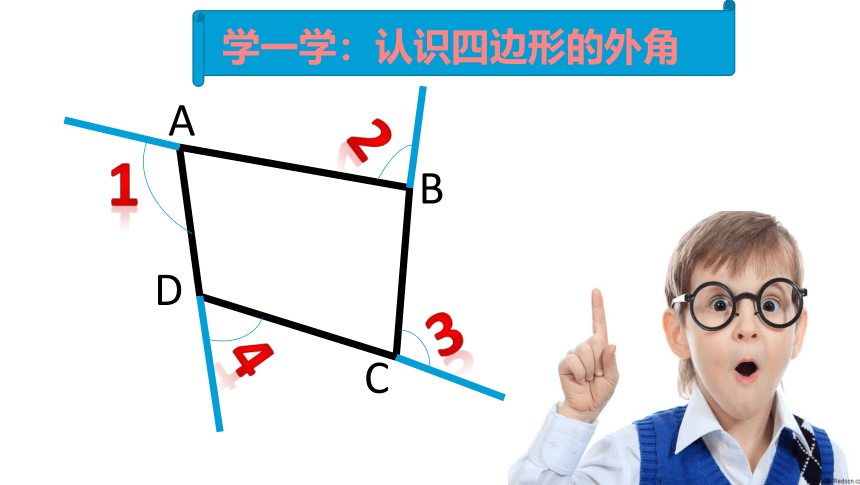
学一学:认识四边形的外角
A
B
C
D
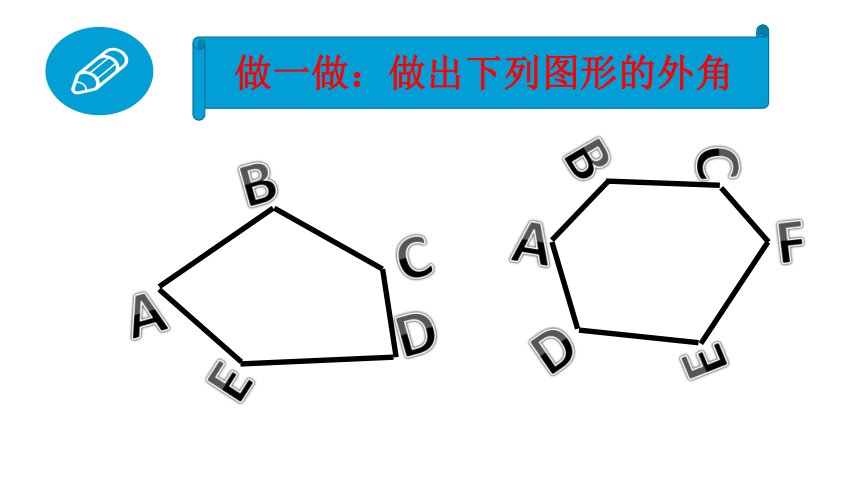
做一做:做出下列图形的外角
D
B
C
A
E
A
B
C
D
E
F
YOUR COMOANY’S NAME
师公开课PPT模版
适用于商务总结/工作总结/工作计划
2019
问题二:
回忆上学期我们在做课后习题学过的三角形的外角和是多少?是通过什么方法来计算三角形的外角和的?
问 题 一:上节课我们学习了多边形的内角和公式:
(n-2)X180°
03
合作探究 感悟新知
问题三:
老师手中的三角形内角和是多少度?
那么它的外角和是多少度呢?
求
3
1
2
<1+<2+<3=( )°
从内角和转化为外角和
A
B
C
A
B
C
从简单情形开始
方法一:构造平角
1、先把三角形的三个外角和三个内角这六个角的和求出来,刚好是三个平角
2、再用这六个角的和减去三个内角的和,剩下的就是三角形的外角和了 .
方法二:作平行线
把三个外角集中到一起
1
2
3
1
2
外角
内角
探 究 创 新 一:三角形外角和
即:<1+<2+<3=360°
即:180°x 3 – 180°=360°
A
B
C
A
B
C
平行线做法探究:
集中到顶点
集中到边上
集中到内部
集中到外部
1
1
1
1
2
2
3
2
2
3
3
3
2
1
3
2
1
3
3
2
1
2
得到:<1+<2+<3=360°
那么四边形的外角和呢?
从简单情形开始
1
A
B
C
A
B
C
A
B
C
A
B
C
从简单情形开始
探 究 创 新 二:四边形外角和
方法一:构造平角
<1+<2+<3+<4=
4X180°—360°=360°
1
2
3
4
1
3
4
2
方法二:作平行线构造周角
<1+<2+<3+<4=360°
(刚好一周)
1
2
3
4
C
B
C
D
A
B
A
D
探 究 创 新 三
如图:小刚沿一个五边形广场周围的小路,按逆时针方向跑步。
(1)小刚每从一条小路转到下一条小路时,跑步方向改变的角是哪个角?在图上标出这些角。
(2)他每跑完一圈,跑步方向改变的角一共有几个,他们的内角和是多少?
归纳得到猜想
A
E
D
B
C
D
C
A
1
E
B
方法一:构造平角
2
3
4
5
<1+ <2+ < 3+ <4+ <5
=180°x5 -540°=360°
方法二:做平行线构造周角
猜想:多边形的外角和都等于360°
04
探究归纳 方法小结
证明猜想:(n 边形外角和)
外角和=(n个平角的和) –( 内角)和
n x 180°- (n – 2 )x180°
=n x 180°- n x 180°+2 x 180°
=360°
我们刚才用( )方法把
体现( 转化 )的数学思想
多边形的外角
平角或周角
转化
探究归纳小结
转化
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}图 形
边 数
内角和与外角和总值
内角和
外角和
3
3 x 180 °
1 x 180 °
2x 180 °=360°
4
4 x 180 °
2 x 180 °
2x 180 °=360°
5
5 x 180 °
3 x 180 °
2x 180 °=360°
n 边形
n
n x 180 °
(n - 2) x 180 °
2x 180 °=360°
归纳:
问题四:求图中正五边形一个内角的度数?
1、三角形外角和等于360°;
2、四边形外角和等于360°;
3、五边形外角和等于360°;
4、n边形外角和等于360°。
结论:任意多边形的外角和等于360°
01
一个多边形的内角和是外角和的2倍,它是几边形?如果这个多边形的每个内角都相等,那么每个内角等于多少度?
是否存在一个多边形,它的每个外角都等于内角的1/5?简述你的理由?
03
若两个多边形的边数相差1,则它们的内角和、外角和分别有什么异同?
04
02
随堂检测
一个多边形的每个外角都等于与它相邻的内角,这个多边形是几边形?能确定它的每个外角的度数吗?
课堂小结
通过本节课的学习,你学到了哪些知识?有何体会?
01
多边形外角的定义;
02
求多边形外角和的方法(两种方法);
04
多边形外角 转化 平角或周角(转化的思想)。
03
多边形的外角和 360°;
第 六 章
6·4 多边形的外角和
第二课时
北师大版八年级数学下册
目 录
CONTENTS
1
2
3
4
创设情境 激发兴趣
温故知新 理解概念
合作探究 感悟新知
探究归纳 课堂小结
01
创设情境 激发兴趣
看一看
02
温故知新 理解概念
外角的定义:多边形内角的一边与另一边的反向延长线所组成的角
顶点
内角
边
A
B
C
以三边形为例,认识多边形的外角
1
2
3
三角形外角的定义:
四边形外角的定义:
ABCD内角的一边与另一边的反向延长线组成的角,成为 ABCD的外角。
五边形外角的定义:
ABCDE内角的一边与另一边的反向延长线组成的角,成为
ABCDE的外角。
N边形外角的定义:
N边形内角的一边与另一边的反向延长线组成的角,成N边形的外角。
n边形外角定义呢?
?ABC内角的一边与另一边的反向延长线组成的角,成为?ABC的外角。
1
2
3
4
学一学:认识四边形的外角
A
B
C
D
做一做:做出下列图形的外角
D
B
C
A
E
A
B
C
D
E
F
YOUR COMOANY’S NAME
师公开课PPT模版
适用于商务总结/工作总结/工作计划
2019
问题二:
回忆上学期我们在做课后习题学过的三角形的外角和是多少?是通过什么方法来计算三角形的外角和的?
问 题 一:上节课我们学习了多边形的内角和公式:
(n-2)X180°
03
合作探究 感悟新知
问题三:
老师手中的三角形内角和是多少度?
那么它的外角和是多少度呢?
求
3
1
2
<1+<2+<3=( )°
从内角和转化为外角和
A
B
C
A
B
C
从简单情形开始
方法一:构造平角
1、先把三角形的三个外角和三个内角这六个角的和求出来,刚好是三个平角
2、再用这六个角的和减去三个内角的和,剩下的就是三角形的外角和了 .
方法二:作平行线
把三个外角集中到一起
1
2
3
1
2
外角
内角
探 究 创 新 一:三角形外角和
即:<1+<2+<3=360°
即:180°x 3 – 180°=360°
A
B
C
A
B
C
平行线做法探究:
集中到顶点
集中到边上
集中到内部
集中到外部
1
1
1
1
2
2
3
2
2
3
3
3
2
1
3
2
1
3
3
2
1
2
得到:<1+<2+<3=360°
那么四边形的外角和呢?
从简单情形开始
1
A
B
C
A
B
C
A
B
C
A
B
C
从简单情形开始
探 究 创 新 二:四边形外角和
方法一:构造平角
<1+<2+<3+<4=
4X180°—360°=360°
1
2
3
4
1
3
4
2
方法二:作平行线构造周角
<1+<2+<3+<4=360°
(刚好一周)
1
2
3
4
C
B
C
D
A
B
A
D
探 究 创 新 三
如图:小刚沿一个五边形广场周围的小路,按逆时针方向跑步。
(1)小刚每从一条小路转到下一条小路时,跑步方向改变的角是哪个角?在图上标出这些角。
(2)他每跑完一圈,跑步方向改变的角一共有几个,他们的内角和是多少?
归纳得到猜想
A
E
D
B
C
D
C
A
1
E
B
方法一:构造平角
2
3
4
5
<1+ <2+ < 3+ <4+ <5
=180°x5 -540°=360°
方法二:做平行线构造周角
猜想:多边形的外角和都等于360°
04
探究归纳 方法小结
证明猜想:(n 边形外角和)
外角和=(n个平角的和) –( 内角)和
n x 180°- (n – 2 )x180°
=n x 180°- n x 180°+2 x 180°
=360°
我们刚才用( )方法把
体现( 转化 )的数学思想
多边形的外角
平角或周角
转化
探究归纳小结
转化
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}图 形
边 数
内角和与外角和总值
内角和
外角和
3
3 x 180 °
1 x 180 °
2x 180 °=360°
4
4 x 180 °
2 x 180 °
2x 180 °=360°
5
5 x 180 °
3 x 180 °
2x 180 °=360°
n 边形
n
n x 180 °
(n - 2) x 180 °
2x 180 °=360°
归纳:
问题四:求图中正五边形一个内角的度数?
1、三角形外角和等于360°;
2、四边形外角和等于360°;
3、五边形外角和等于360°;
4、n边形外角和等于360°。
结论:任意多边形的外角和等于360°
01
一个多边形的内角和是外角和的2倍,它是几边形?如果这个多边形的每个内角都相等,那么每个内角等于多少度?
是否存在一个多边形,它的每个外角都等于内角的1/5?简述你的理由?
03
若两个多边形的边数相差1,则它们的内角和、外角和分别有什么异同?
04
02
随堂检测
一个多边形的每个外角都等于与它相邻的内角,这个多边形是几边形?能确定它的每个外角的度数吗?
课堂小结
通过本节课的学习,你学到了哪些知识?有何体会?
01
多边形外角的定义;
02
求多边形外角和的方法(两种方法);
04
多边形外角 转化 平角或周角(转化的思想)。
03
多边形的外角和 360°;
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
