北师大版八年级下册数学1.3 线段的垂直平分线(2)课件(共16张PPT)
文档属性
| 名称 | 北师大版八年级下册数学1.3 线段的垂直平分线(2)课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 624.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-03 14:36:32 | ||
图片预览




文档简介
第一章 三角形的证明
北师大版数学八年级下册
1.3 线段的垂直平分线(2)
郑州市第七十一中学
等腰
三角形
……
性质
判定
等边对等角
三线合一
等角对等边
特例
等
边
三
角
形
勾股定理
勾股定理逆定理
两锐角互余
有一个直角
直角
三角形
线段的
垂直平分线
性质
判定
性质
判定
作法
三
角
形
的
证
明
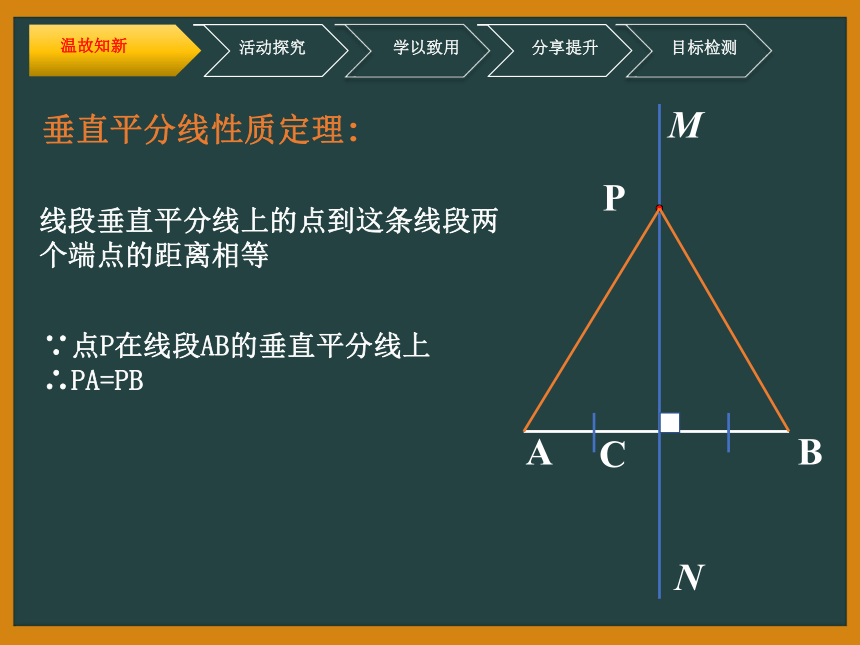
垂直平分线性质定理:
线段垂直平分线上的点到这条线段两个端点的距离相等
∵点P在线段AB的垂直平分线上
∴PA=PB
A
B
P
M
N
C
活动探究 学以致用 分享提升 目标检测
温故知新
垂直平分线判定定理:
到一条线段两个端点的距离相等的点,在这条线段的垂直平分线上
∵PA=PB
∴点P在线段AB的垂直平分线上
P
A
B
活动探究 学以致用 分享提升 目标检测
温故知新
A
B
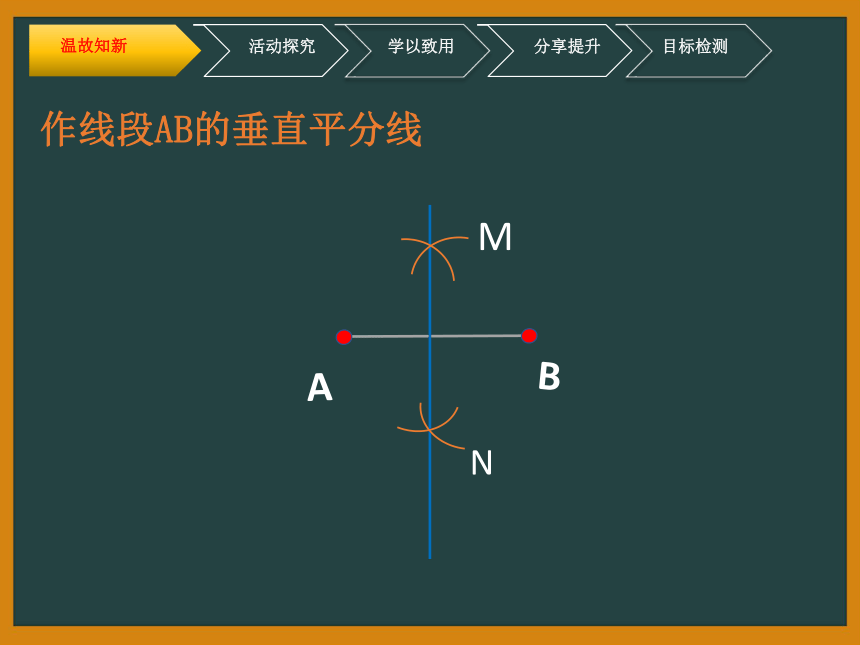
作线段AB的垂直平分线
M
N
活动探究 学以致用 分享提升 目标检测
温故知新
学习目标:
1.通过动手操作、尺规作图和理论证明,能探究出“三角形三边垂直平分线的性质”,体会证明的必要性,并会熟练应用它来解决实际问题.
2.借助线段垂直平分线的尺规作图,通过个人探究、小组交流,能利用线段的垂直平分线较快作出符合条件的几何图形,体会转化的思想.
活动一:
折一折:拿出准备好的三角形纸片,通过折叠找出每条边的垂直平分线(画出折痕),观察这三条垂直平分线,你发现了什么?
学习要求:
1.自主完成
2.组内交流
3.用时:2分钟。
活动探究 学以致用 分享提升 目标检测
温故知新
活动一:
画一画:请利用尺规作三角形三条边的垂直平分线,观察这三条垂直平分线,和你刚才的发现一样吗?
活动要求:
1.自主完成
2.组内交流
3.用时:3分钟。
活动探究 学以致用 分享提升 目标检测
温故知新
活动一:(证一证)
已知:在△ABC中设AB、BC的垂直平分线交于点P.
求证:边AC的垂直平分线经过点P,且PA=PB=PC.
证明: ∵点P在线段AB的垂直平分线上,
∴PA=PB.
同理PB=PC.
∴PA=PB=PC.
∴P点在AC的垂直平分线上
(到线段两个端点距离相等的点在这条线段的垂直平分线上).
即 边AC的垂直平分线经过点P.
活动探究 学以致用 分享提升 目标检测
温故知新
C
B
A
P
活动二:已知三角形的一条边为5cm及这条边上的高3cm,你能作出三角形吗?如果能,请作在学案上.
活动要求:1.自主完成
2.组内交流
3.用时:2分钟。
活动探究 学以致用 分享提升 目标检测
温故知新
活动二:已知等腰三角形的底边为5cm及底边上的高3cm,你能作出三角形吗?如果能,你作出的三角形还和同伴的不同吗?
已知:线段a、h
求作:△ABC,使AB=AC,且BC=a,高AD=h
a
h
活动探究 学以致用 分享提升 目标检测
温故知新
活动要求:1.独立完成
2.代表展示
3.用时:3分钟。
活动三:
已知直线 l 和 l 上一点 P,用尺规作 l 的垂线,使它经过点 P .
? 已知直线 l 和 l 外一点 P, 用尺规作 l 的垂线,使它经过点 P .
活动要求:
1.自主完成
2.代表展示
3.用时:5分钟。
活动探究 学以致用 分享提升 目标检测
温故知新
如图△ABC,求作:
(1)AC 边上的高;
(2)BC边上的高
活动探究 学以致用 分享提升 目标检测
温故知新
等腰
三角形
……
性质
判定
等边对等角
三线合一
等角对等边
特例
等
边
三
角
形
勾股定理
勾股定理逆定理
两锐角互余
有一个直角
直角
三角形
线段的
垂直平分线
性质
判定
判定
性质
作法
……
1.(检测目标一)如图,已知线段a,求作以a为底边,以 为高的等腰三角形.这个等腰三角形有什么特征?
2.(检测目标二)我校为举办第二届青少年文化周活动,打算在学校操场搭建大型展演舞台.在选址过程中,为保证同学们观看效果,舞台位置P应当与三个年级同学所坐位置(如图中A,B,C表示)的距离相等.如果∠ABC为直角,请你在图中找出点P的位置.
?
?
?
A
C
B
活动探究 学以致用 分享提升 目标检测
温故知新
a
作业设计
1.请你找出生活中哪些设计会用到线段的垂直平分线的相关知识。
2.尝试利用线段垂直平分线的尺规作图探究角平分线的尺规作图理论依据。
郑州市第七十一中学
北师大版数学八年级下册
1.3 线段的垂直平分线(2)
郑州市第七十一中学
等腰
三角形
……
性质
判定
等边对等角
三线合一
等角对等边
特例
等
边
三
角
形
勾股定理
勾股定理逆定理
两锐角互余
有一个直角
直角
三角形
线段的
垂直平分线
性质
判定
性质
判定
作法
三
角
形
的
证
明
垂直平分线性质定理:
线段垂直平分线上的点到这条线段两个端点的距离相等
∵点P在线段AB的垂直平分线上
∴PA=PB
A
B
P
M
N
C
活动探究 学以致用 分享提升 目标检测
温故知新
垂直平分线判定定理:
到一条线段两个端点的距离相等的点,在这条线段的垂直平分线上
∵PA=PB
∴点P在线段AB的垂直平分线上
P
A
B
活动探究 学以致用 分享提升 目标检测
温故知新
A
B
作线段AB的垂直平分线
M
N
活动探究 学以致用 分享提升 目标检测
温故知新
学习目标:
1.通过动手操作、尺规作图和理论证明,能探究出“三角形三边垂直平分线的性质”,体会证明的必要性,并会熟练应用它来解决实际问题.
2.借助线段垂直平分线的尺规作图,通过个人探究、小组交流,能利用线段的垂直平分线较快作出符合条件的几何图形,体会转化的思想.
活动一:
折一折:拿出准备好的三角形纸片,通过折叠找出每条边的垂直平分线(画出折痕),观察这三条垂直平分线,你发现了什么?
学习要求:
1.自主完成
2.组内交流
3.用时:2分钟。
活动探究 学以致用 分享提升 目标检测
温故知新
活动一:
画一画:请利用尺规作三角形三条边的垂直平分线,观察这三条垂直平分线,和你刚才的发现一样吗?
活动要求:
1.自主完成
2.组内交流
3.用时:3分钟。
活动探究 学以致用 分享提升 目标检测
温故知新
活动一:(证一证)
已知:在△ABC中设AB、BC的垂直平分线交于点P.
求证:边AC的垂直平分线经过点P,且PA=PB=PC.
证明: ∵点P在线段AB的垂直平分线上,
∴PA=PB.
同理PB=PC.
∴PA=PB=PC.
∴P点在AC的垂直平分线上
(到线段两个端点距离相等的点在这条线段的垂直平分线上).
即 边AC的垂直平分线经过点P.
活动探究 学以致用 分享提升 目标检测
温故知新
C
B
A
P
活动二:已知三角形的一条边为5cm及这条边上的高3cm,你能作出三角形吗?如果能,请作在学案上.
活动要求:1.自主完成
2.组内交流
3.用时:2分钟。
活动探究 学以致用 分享提升 目标检测
温故知新
活动二:已知等腰三角形的底边为5cm及底边上的高3cm,你能作出三角形吗?如果能,你作出的三角形还和同伴的不同吗?
已知:线段a、h
求作:△ABC,使AB=AC,且BC=a,高AD=h
a
h
活动探究 学以致用 分享提升 目标检测
温故知新
活动要求:1.独立完成
2.代表展示
3.用时:3分钟。
活动三:
已知直线 l 和 l 上一点 P,用尺规作 l 的垂线,使它经过点 P .
? 已知直线 l 和 l 外一点 P, 用尺规作 l 的垂线,使它经过点 P .
活动要求:
1.自主完成
2.代表展示
3.用时:5分钟。
活动探究 学以致用 分享提升 目标检测
温故知新
如图△ABC,求作:
(1)AC 边上的高;
(2)BC边上的高
活动探究 学以致用 分享提升 目标检测
温故知新
等腰
三角形
……
性质
判定
等边对等角
三线合一
等角对等边
特例
等
边
三
角
形
勾股定理
勾股定理逆定理
两锐角互余
有一个直角
直角
三角形
线段的
垂直平分线
性质
判定
判定
性质
作法
……
1.(检测目标一)如图,已知线段a,求作以a为底边,以 为高的等腰三角形.这个等腰三角形有什么特征?
2.(检测目标二)我校为举办第二届青少年文化周活动,打算在学校操场搭建大型展演舞台.在选址过程中,为保证同学们观看效果,舞台位置P应当与三个年级同学所坐位置(如图中A,B,C表示)的距离相等.如果∠ABC为直角,请你在图中找出点P的位置.
?
?
?
A
C
B
活动探究 学以致用 分享提升 目标检测
温故知新
a
作业设计
1.请你找出生活中哪些设计会用到线段的垂直平分线的相关知识。
2.尝试利用线段垂直平分线的尺规作图探究角平分线的尺规作图理论依据。
郑州市第七十一中学
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
