北师大版八年级下册数学2.2 不等式的基本性质课件(共28张PPT)
文档属性
| 名称 | 北师大版八年级下册数学2.2 不等式的基本性质课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 835.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-03 14:19:37 | ||
图片预览








文档简介
八年级数学·下 新课标 [北师大版]
第二章 一元一次不等式与
一元一次不等式组
2.2 不等式的基本性质
如果a=b,那么
温故知新
=
=
=
=
回顾:等式的基本性质
等式
不等式
等式两边同时加上(或减去)同一个数或整式,所得结果仍是等式.
基本性质2
基本性质1
等式的两边同时乘同一个数(或除以一个不为0的数),所得结果仍是等式.
?
?
情景游戏
两人同登台阶比身高
对比“等式基本性质1”,你有什么想法?
为了验证不等式的性质,我们可以从一些数字的运算开始.用“<”或“>”完成下列两组填空,你能得出不等式性质1了吗?
① 5>3
5+2 3+2, 5+(-2) 3+(-2),
5+0 3+0 ;
② -1<3
-1+2 3+2,-1+(-3) 3+(-3),
-1+0 3+0.
>
>
>
<
<
<
探究一 不等式的性质1
比一比
等式
不等式
等式两边都加上(或减去)同一个数或整式,所得结果仍是等式.
基本性质2
基本性质1
等式的两边都乘同一个数(或除以一个不为0的数),所得结果仍是等式.
?
不等式两边都加上(或减去)同一个整式,不等号的方向不变。
探究二 不等式的性质
比一比
等式
不等式
等式两边都加上(或减去)同一个数或整式,所得结果仍是等式.
基本性质2
基本性质1
等式的两边都乘同一个数(或除以一个不为0的数),所得结果仍是等式.
不等式两边都加上(或减去)同一个整式,不等号的方向不变。
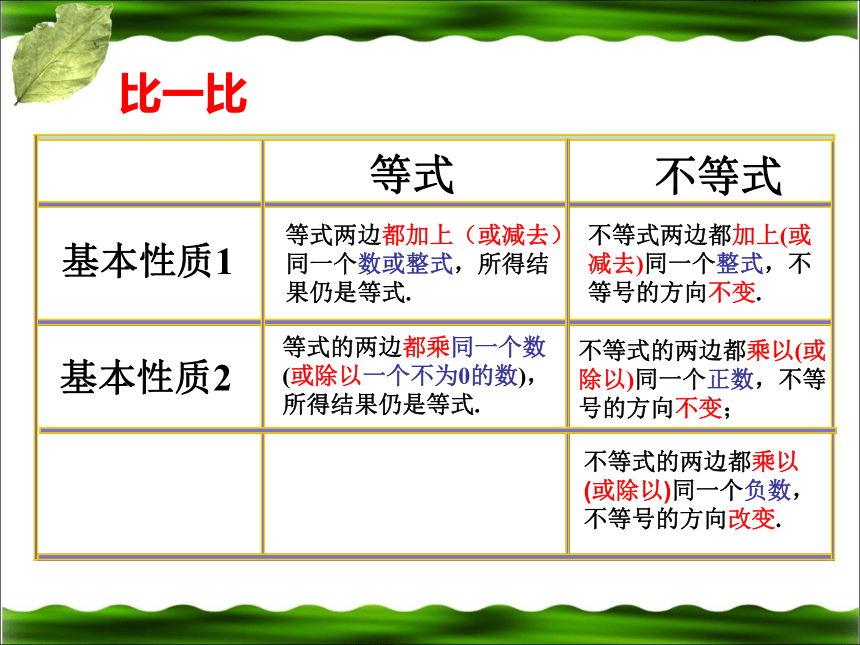
比一比
等式
不等式
等式两边都加上(或减去)同一个数或整式,所得结果仍是等式.
基本性质2
基本性质1
等式的两边都乘同一个数(或除以一个不为0的数),所得结果仍是等式.
不等式两边都加上(或减去)同一个整式,不等号的方向不变.
不等式的两边都乘以(或除以)同一个正数,不等号的方向不变;
不等式的两边都乘以(或除以)同一个负数,不等号的方向改变.
不等式性质与等式性质有什么异同
相同点
不同点
等式与不等式都可以在它的两边加上或减去同一个整式,符号保持不变.
等式与不等式两边同乘或同除以同一个正数,符号保持不变.
不等式两边同乘或同除以同一个负数,不等号的方向改变.
范例讲解
例1、将下列不等式化成“x>a”或“x解:
(1)根据不等式性质1,两边都加上5,得
即
(2)根据不等式性质3,两边都除以–2,得
即
数学是符号加逻辑—罗素
一
已知a”填空:
二
二
已知x>y,下列不等式一定成立吗?
x
x
√
x
三
已知a<b,且ma>mb.求m的取值范围
四
若关于x的不等式(m-1)x>m-1可变形为x<1,求字母m的取值范围。
拓展:利用不等式的基本性质比较大小
已知a>4.
(1)比较a2+1与4a+1的大小;
(2)比较ab与4b的大小.
分析:(1)a>4→两边都乘a(a>4>0)→应用不等式的基本性质2→比较a2与4a的大小→两边都加1→应用不等式的基本性质1→比较a2+1与4a+1的大小.
(2)a>4→两边都乘b(b的正负情况)→应用不等式的基本性质2→比较ab与4b的大小.
解:(1)因为a>4>0,所以根据不等式的基本性质2,不等式a>4的两边都乘a,得a2>4a.根据不等式的基本性质1,不等式a2>4a两边都加1,得a2+1>4a+1.
(2)因为a>4,所以当b>0时,根据不等式的基本性质2,不等式a>4的两边都乘b,得ab>4b;当b=0时,ab=4b;当b<0时,根据不等式的基本性质3,不等式a>4的两边都乘b,得ab<4b.
我今天学到了
……
你今天这节课有什么收获呢?
第二节 不等式的基本性质
作业
习题2.2
第二节 不等式的基本性质
第二章 一元一次不等式与
一元一次不等式组
2.2 不等式的基本性质
如果a=b,那么
温故知新
=
=
=
=
回顾:等式的基本性质
等式
不等式
等式两边同时加上(或减去)同一个数或整式,所得结果仍是等式.
基本性质2
基本性质1
等式的两边同时乘同一个数(或除以一个不为0的数),所得结果仍是等式.
?
?
情景游戏
两人同登台阶比身高
对比“等式基本性质1”,你有什么想法?
为了验证不等式的性质,我们可以从一些数字的运算开始.用“<”或“>”完成下列两组填空,你能得出不等式性质1了吗?
① 5>3
5+2 3+2, 5+(-2) 3+(-2),
5+0 3+0 ;
② -1<3
-1+2 3+2,-1+(-3) 3+(-3),
-1+0 3+0.
>
>
>
<
<
<
探究一 不等式的性质1
比一比
等式
不等式
等式两边都加上(或减去)同一个数或整式,所得结果仍是等式.
基本性质2
基本性质1
等式的两边都乘同一个数(或除以一个不为0的数),所得结果仍是等式.
?
不等式两边都加上(或减去)同一个整式,不等号的方向不变。
探究二 不等式的性质
比一比
等式
不等式
等式两边都加上(或减去)同一个数或整式,所得结果仍是等式.
基本性质2
基本性质1
等式的两边都乘同一个数(或除以一个不为0的数),所得结果仍是等式.
不等式两边都加上(或减去)同一个整式,不等号的方向不变。
比一比
等式
不等式
等式两边都加上(或减去)同一个数或整式,所得结果仍是等式.
基本性质2
基本性质1
等式的两边都乘同一个数(或除以一个不为0的数),所得结果仍是等式.
不等式两边都加上(或减去)同一个整式,不等号的方向不变.
不等式的两边都乘以(或除以)同一个正数,不等号的方向不变;
不等式的两边都乘以(或除以)同一个负数,不等号的方向改变.
不等式性质与等式性质有什么异同
相同点
不同点
等式与不等式都可以在它的两边加上或减去同一个整式,符号保持不变.
等式与不等式两边同乘或同除以同一个正数,符号保持不变.
不等式两边同乘或同除以同一个负数,不等号的方向改变.
范例讲解
例1、将下列不等式化成“x>a”或“x
(1)根据不等式性质1,两边都加上5,得
即
(2)根据不等式性质3,两边都除以–2,得
即
数学是符号加逻辑—罗素
一
已知a
二
二
已知x>y,下列不等式一定成立吗?
x
x
√
x
三
已知a<b,且ma>mb.求m的取值范围
四
若关于x的不等式(m-1)x>m-1可变形为x<1,求字母m的取值范围。
拓展:利用不等式的基本性质比较大小
已知a>4.
(1)比较a2+1与4a+1的大小;
(2)比较ab与4b的大小.
分析:(1)a>4→两边都乘a(a>4>0)→应用不等式的基本性质2→比较a2与4a的大小→两边都加1→应用不等式的基本性质1→比较a2+1与4a+1的大小.
(2)a>4→两边都乘b(b的正负情况)→应用不等式的基本性质2→比较ab与4b的大小.
解:(1)因为a>4>0,所以根据不等式的基本性质2,不等式a>4的两边都乘a,得a2>4a.根据不等式的基本性质1,不等式a2>4a两边都加1,得a2+1>4a+1.
(2)因为a>4,所以当b>0时,根据不等式的基本性质2,不等式a>4的两边都乘b,得ab>4b;当b=0时,ab=4b;当b<0时,根据不等式的基本性质3,不等式a>4的两边都乘b,得ab<4b.
我今天学到了
……
你今天这节课有什么收获呢?
第二节 不等式的基本性质
作业
习题2.2
第二节 不等式的基本性质
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
