北师大版八年级下册数学3.2图形的旋转 图形的旋转作图课件(共15张PPT)
文档属性
| 名称 | 北师大版八年级下册数学3.2图形的旋转 图形的旋转作图课件(共15张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-03 14:37:40 | ||
图片预览





文档简介
图形的旋转(2)
1、“旋转”的定义:
在平面内,将一个图形绕着一个定点沿某
个方向转动一个角度,这样的图形运动称为旋
转(变换)。
2、“旋转”的基本性质:
(1)经过旋转,图形的形状和大小不变;
(2)经过旋转,图形上的每一点都绕旋转中心沿相
同的方向转动了相同的角度;
(3)任意一对对应点与旋转中心的连线所成的角都是旋转角,对应点到旋转中心的距离相等。
观察下列动画:
O
(1)将“小旗子”绕点O按顺时针方向旋转90°后,
图形有什么变化?
(2)你能画出旋转后的“小旗子”吗?
旋转90°后,图形形状和大小没有变化,位置发生变化.
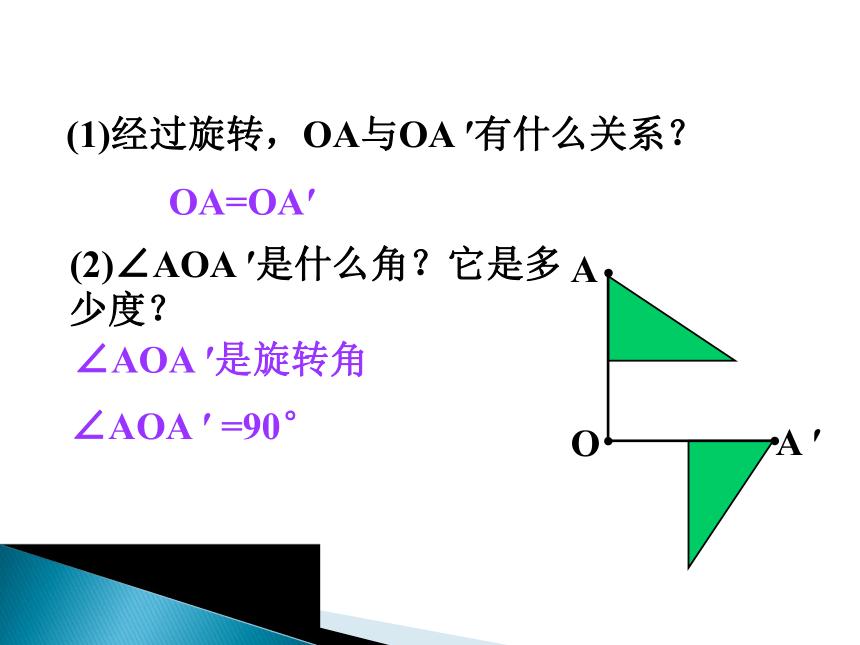
(1)经过旋转,OA与OA ′有什么关系?
O
A
A ′
(2)∠AOA ′是什么角?它是多少度?
OA=OA′
∠AOA ′是旋转角
∠AOA ′ =90°
“旋转对应点”的作法 :
(1) 将关键点A与旋转中心O连接;
(2) 以OA为始边在旋转方向作一个角等于旋转角;
(3) 在角的终边上截取点A′,使OA ′ =OA;
(4) 点A ′就是点A的旋转对应点。
(5)顺次将OB,OC也旋转90°
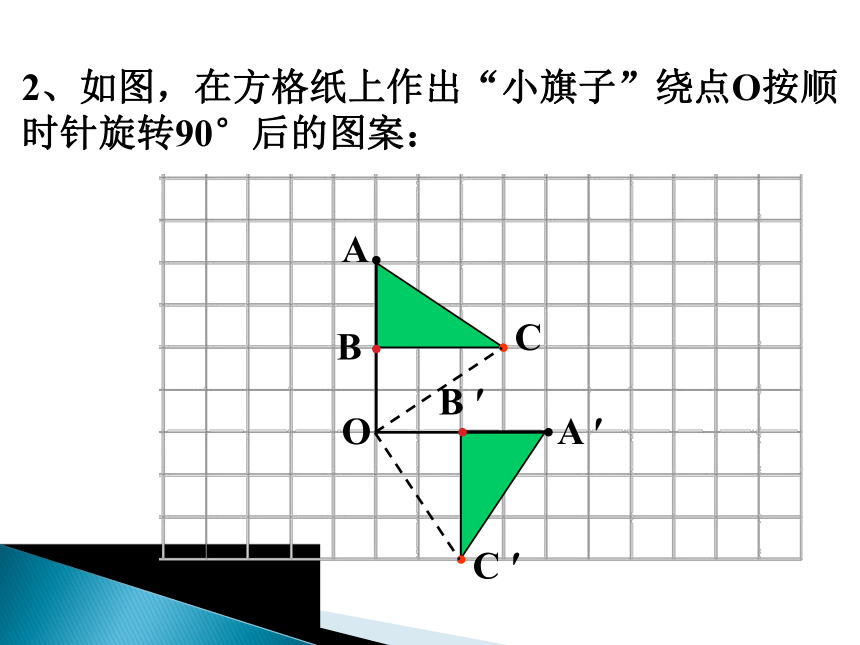
2、如图,在方格纸上作出“小旗子”绕点O按顺
时针旋转90°后的图案:
O
A
A ′
B
B ′
C
C ′
新知归纳
“旋转”作图的步骤 :
(1)明确题目要求:
弄清旋转中心、方向和角度;
(2)分析所作图形:
找出构成图形的关键点;
(3)旋转关键点:
沿一定的方向和角度分别作出
各关键点;
(4)作出新图形:
顺次连接各关键点;
*
1.如图,△ABC绕点O旋转后,顶点 A的对应点为点D。试确定顶点B的对应点的位置,以及 旋转后的三角形。
C
A
B
D
O
分析
一般旋转作图题,首先明白旋转的方向与角度.
顶点 A的对应点为点D,旋转角就是∠AOD .△ABC绕点O旋转后的三角形.根据旋转的性质知道:经过旋转,图形上的每一点都绕旋转中心沿相同方向转动了相同的角度,即旋转角相等,对应点到旋转中心的距离相等,则∠BOE=∠COF=∠AOD,OE=OB,OF=OC,这样即可求作出旋转后的图形.
点拨:旋转角是( )
*
C
A
B
D
O
F
E
解:做法:
(1)连接OA,OD,OB,OC.
(2)如下图,分别以OB、OC为一边作 ∠BOE、∠COF,使得∠BOE=∠COF=∠AOD.
(3)分别在射线OE、OF上截取
OE=OB、OF=OC.
(4)连接EF,ED,FD.
△DEF,就是△ABC绕O
点旋转后的图形.
2.议一议 本题还有没有其他作法,可以作出△ABC绕O点旋转后的图形△DEF吗?
点拨:做全等三角形
1.可以先作出点B的对应点E,连接DE,然后以点D、E为圆心,分别以AC、BC为半径画弧,两弧交于点F,连接DF,EF,则△DEF就是△ABC绕点O旋转后的图形.
2.也可以先作出点C的对应点F,然后连接DF.因为△ABC与△DEF全等,所以既可以用两边夹角,也可以用两角夹边,找到点B的对应点E,即△DEF.
3、如图,四边形ABCD绕O点旋转后,顶点A的对应点为E,试确定B、C、D对应的点的位置,以及旋转后的四边形.
解 (1)连接OA、OB、OC、OD、OE.
(2) 分别以OB、OC、OD为一边作∠BOF, ∠COG, ∠DOH,使∠BOF= ∠COG= ∠DOH= ∠AOE.
(3)分别在射线OF,OG,OH上,截取OF=OB,OG=OC,OH=OD
(4)连接EF,FG,GH,HE.
四边形EFGH就是四边形ABCD绕O点旋转后的图形。
APA…**.B.*.`..*
A
B
C
O
做出△ABC绕点O点顺时针旋转60度的图形.写出做法,保留作图痕迹.
.
应用拓展
1、“旋转对应点”的作法 :以点A为例
(1) 将关键点A与旋转中心O连接;
(2) 以OA为始边在旋转方向作一个角等于旋转角;
(3) 在角的终边上截取点A′,使OA ′ =OA;
(4) 点A ′就是点A的旋转对应点。
2、“旋转”作图的步骤 :
(1)明确题目要求:
弄清旋转中心、方向和角度;
(2)分析所作图形:
找出构成图形的关键点;
(3)旋转关键点:
沿一定的方向和角度分别作出
各关键点;
(4)作出新图形:
顺次连接各关键点;
(5)写出结论:
说明所作出的图形。
1.从教材习题中选取
2.完成练习册本课时的习题
布置作业
1、“旋转”的定义:
在平面内,将一个图形绕着一个定点沿某
个方向转动一个角度,这样的图形运动称为旋
转(变换)。
2、“旋转”的基本性质:
(1)经过旋转,图形的形状和大小不变;
(2)经过旋转,图形上的每一点都绕旋转中心沿相
同的方向转动了相同的角度;
(3)任意一对对应点与旋转中心的连线所成的角都是旋转角,对应点到旋转中心的距离相等。
观察下列动画:
O
(1)将“小旗子”绕点O按顺时针方向旋转90°后,
图形有什么变化?
(2)你能画出旋转后的“小旗子”吗?
旋转90°后,图形形状和大小没有变化,位置发生变化.
(1)经过旋转,OA与OA ′有什么关系?
O
A
A ′
(2)∠AOA ′是什么角?它是多少度?
OA=OA′
∠AOA ′是旋转角
∠AOA ′ =90°
“旋转对应点”的作法 :
(1) 将关键点A与旋转中心O连接;
(2) 以OA为始边在旋转方向作一个角等于旋转角;
(3) 在角的终边上截取点A′,使OA ′ =OA;
(4) 点A ′就是点A的旋转对应点。
(5)顺次将OB,OC也旋转90°
2、如图,在方格纸上作出“小旗子”绕点O按顺
时针旋转90°后的图案:
O
A
A ′
B
B ′
C
C ′
新知归纳
“旋转”作图的步骤 :
(1)明确题目要求:
弄清旋转中心、方向和角度;
(2)分析所作图形:
找出构成图形的关键点;
(3)旋转关键点:
沿一定的方向和角度分别作出
各关键点;
(4)作出新图形:
顺次连接各关键点;
*
1.如图,△ABC绕点O旋转后,顶点 A的对应点为点D。试确定顶点B的对应点的位置,以及 旋转后的三角形。
C
A
B
D
O
分析
一般旋转作图题,首先明白旋转的方向与角度.
顶点 A的对应点为点D,旋转角就是∠AOD .△ABC绕点O旋转后的三角形.根据旋转的性质知道:经过旋转,图形上的每一点都绕旋转中心沿相同方向转动了相同的角度,即旋转角相等,对应点到旋转中心的距离相等,则∠BOE=∠COF=∠AOD,OE=OB,OF=OC,这样即可求作出旋转后的图形.
点拨:旋转角是( )
*
C
A
B
D
O
F
E
解:做法:
(1)连接OA,OD,OB,OC.
(2)如下图,分别以OB、OC为一边作 ∠BOE、∠COF,使得∠BOE=∠COF=∠AOD.
(3)分别在射线OE、OF上截取
OE=OB、OF=OC.
(4)连接EF,ED,FD.
△DEF,就是△ABC绕O
点旋转后的图形.
2.议一议 本题还有没有其他作法,可以作出△ABC绕O点旋转后的图形△DEF吗?
点拨:做全等三角形
1.可以先作出点B的对应点E,连接DE,然后以点D、E为圆心,分别以AC、BC为半径画弧,两弧交于点F,连接DF,EF,则△DEF就是△ABC绕点O旋转后的图形.
2.也可以先作出点C的对应点F,然后连接DF.因为△ABC与△DEF全等,所以既可以用两边夹角,也可以用两角夹边,找到点B的对应点E,即△DEF.
3、如图,四边形ABCD绕O点旋转后,顶点A的对应点为E,试确定B、C、D对应的点的位置,以及旋转后的四边形.
解 (1)连接OA、OB、OC、OD、OE.
(2) 分别以OB、OC、OD为一边作∠BOF, ∠COG, ∠DOH,使∠BOF= ∠COG= ∠DOH= ∠AOE.
(3)分别在射线OF,OG,OH上,截取OF=OB,OG=OC,OH=OD
(4)连接EF,FG,GH,HE.
四边形EFGH就是四边形ABCD绕O点旋转后的图形。
APA…**.B.*.`..*
A
B
C
O
做出△ABC绕点O点顺时针旋转60度的图形.写出做法,保留作图痕迹.
.
应用拓展
1、“旋转对应点”的作法 :以点A为例
(1) 将关键点A与旋转中心O连接;
(2) 以OA为始边在旋转方向作一个角等于旋转角;
(3) 在角的终边上截取点A′,使OA ′ =OA;
(4) 点A ′就是点A的旋转对应点。
2、“旋转”作图的步骤 :
(1)明确题目要求:
弄清旋转中心、方向和角度;
(2)分析所作图形:
找出构成图形的关键点;
(3)旋转关键点:
沿一定的方向和角度分别作出
各关键点;
(4)作出新图形:
顺次连接各关键点;
(5)写出结论:
说明所作出的图形。
1.从教材习题中选取
2.完成练习册本课时的习题
布置作业
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
