北师大版九年级下册数学:3.7 切线长定理 课件(共19张PPT)
文档属性
| 名称 | 北师大版九年级下册数学:3.7 切线长定理 课件(共19张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 499.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-03 14:38:44 | ||
图片预览



文档简介
北师大版九年级数学下册
第三章 圆
3.7 切线长定理
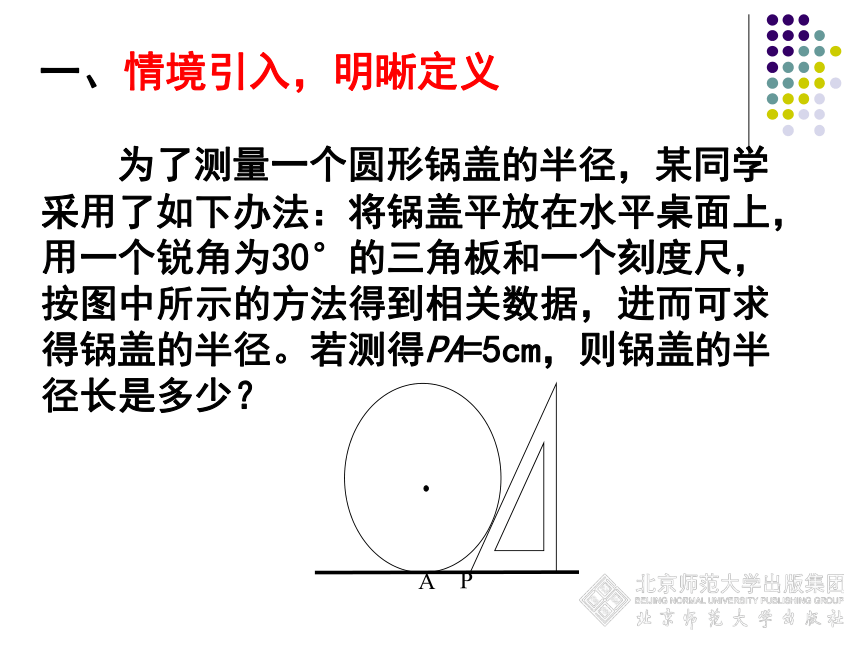
为了测量一个圆形锅盖的半径,某同学采用了如下办法:将锅盖平放在水平桌面上,用一个锐角为30°的三角板和一个刻度尺,按图中所示的方法得到相关数据,进而可求得锅盖的半径。若测得PA=5cm,则锅盖的半径长是多少?
P
A
B
O
一、情境引入,明晰定义
做一做
1、过⊙O外一点P画圆的切线,试试看你
能画出几条?
2、同学们画出的圆的切线是什么线?
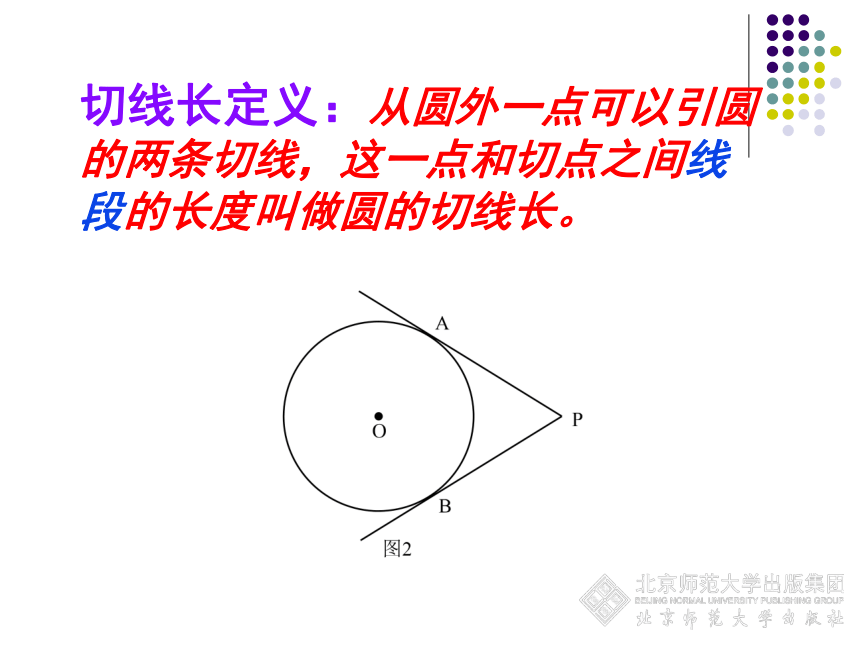
切线长定义:从圆外一点可以引圆的两条切线,这一点和切点之间线段的长度叫做圆的切线长。
1、如图, PA和PB分别与⊙O相切于点A、B ,点P到⊙O的切线长可以用哪一条线段的长来表示?
2、思考:点P到⊙O的
切线有几条?
二、独立思考,大胆判断
线段PA,PB是点P到⊙O的切线长
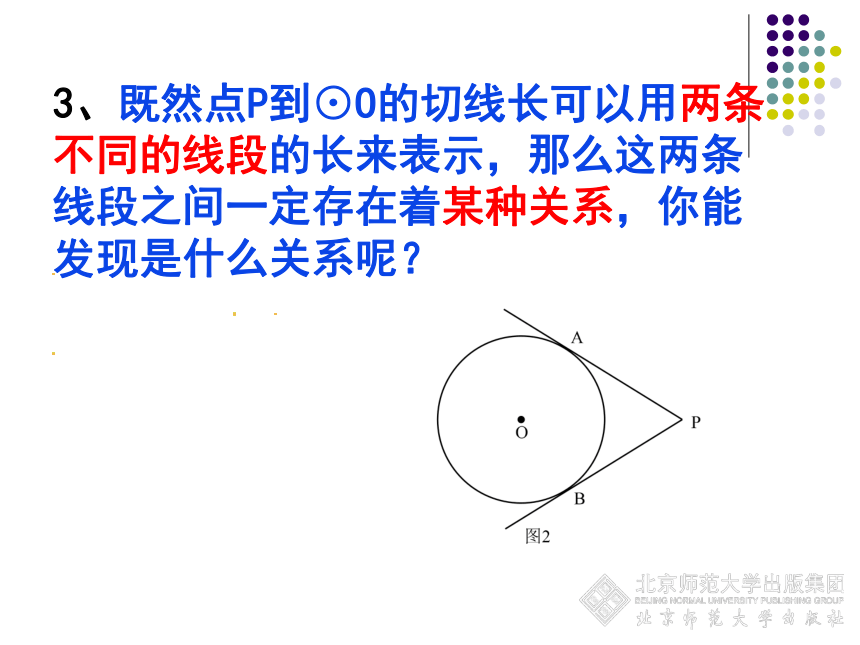
3、既然点P到⊙O的切线长可以用两条不同的线段的长来表示,那么这两条线段之间一定存在着某种关系,你能发现是什么关系呢?
三、探究验证,得出结论
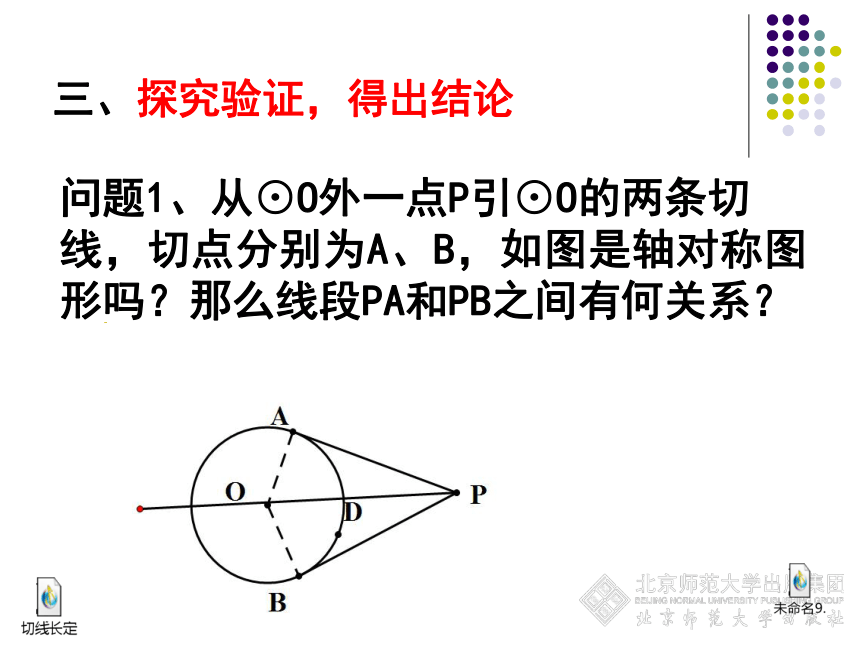
问题1、从⊙O外一点P引⊙O的两条切
线,切点分别为A、B,如图是轴对称图形吗?那么线段PA和PB之间有何关系?
已知:PA、PB分别是⊙O的切线,点A、B分别为切点
求证:PA=PB
问题2:我们猜测的结果能否作为
定理来用呢?为了让我们得出的命
题成为定理,我们需要怎么做?
切线长定理:从圆外一点引圆的两条切线,它们的切线长相等.
1、情景问题 为了测量一个圆形锅盖的半径,某同学采用了如下办法:将锅盖平放在水平桌面上,用一个锐角为30°的三角板和一个刻度尺,按图中所示的方法得到相关数据,进而可求得锅盖的半径。若测得PA=5cm,则锅盖的半径长是多少?
P
A
B
O
四、运用新知,解决问题
问题2、如图,与三角形各边都相切的圆叫做三角形的内切圆,下图中存在切线长定理吗?
问题3:请同学们先在练习本上作
出已知⊙O的四条切线,如图9,
再互相交流与讨论四条切线围成的
四边形(即圆的外切四边形)有什么
性质,发现结论并试着加以说明。
圆的外切四边形对边的关系:
两组对边的和相等.
填空:如图,PA、PB分别与⊙O
相切于点A、B,求:
(1)若PB=12,PO=13,则AO= ( )
(2)若PO=10,AO=6,则PB= ( )
(3)若PA=4,AO=3,
则PO= ;
PD= ;
五、触类旁通,提升能力
已知:如图,Rt△ABC的两条直角边
AC=10,BC=24,⊙O 是△ABC 的内切
圆,切点分别为D,E,F,求⊙O 的半径.
六、课堂小结,畅谈收获
知识上:1、切线长的定义。
2、切线长定理。
3、圆外切四边形边的关系
方法上:观察—猜想—探索—验
证—证明。
情感上:独立思考,迎难而上,乐
于合作,自我评价。
七、推荐作业
A层:已知:如图,⊙O是△ABC的内
切圆,切点分别为D、E、F,
(1)图中共有几对相等线段?
(2)若AF=4,BD=6,CE=8,则
△ABC的周长是 ;
(3)若AB=9,BC=15,AC=12,则
AF= ,BD= ,CE= .
推荐作业
B层
1:已知,如图10,PA、PB分别与⊙O相切于点A、B,PO与⊙O相交于点D,且PA=4cm,PD=2cm.求半径OB的长
2.如图,PA、PB切⊙O于A、B,
PO交AB于E,等式
①AE=BE;②AO2=OE·OP;
③∠OAB=∠APB;
④PA=PB中,成立的有( )
A.1个 B.2个 C.3个 D.4个
教师寄语: 同学们! 请铭记: 勤奋是舟,规律是桨,只有刻苦努力,你们必将顺利抵港。
第三章 圆
3.7 切线长定理
为了测量一个圆形锅盖的半径,某同学采用了如下办法:将锅盖平放在水平桌面上,用一个锐角为30°的三角板和一个刻度尺,按图中所示的方法得到相关数据,进而可求得锅盖的半径。若测得PA=5cm,则锅盖的半径长是多少?
P
A
B
O
一、情境引入,明晰定义
做一做
1、过⊙O外一点P画圆的切线,试试看你
能画出几条?
2、同学们画出的圆的切线是什么线?
切线长定义:从圆外一点可以引圆的两条切线,这一点和切点之间线段的长度叫做圆的切线长。
1、如图, PA和PB分别与⊙O相切于点A、B ,点P到⊙O的切线长可以用哪一条线段的长来表示?
2、思考:点P到⊙O的
切线有几条?
二、独立思考,大胆判断
线段PA,PB是点P到⊙O的切线长
3、既然点P到⊙O的切线长可以用两条不同的线段的长来表示,那么这两条线段之间一定存在着某种关系,你能发现是什么关系呢?
三、探究验证,得出结论
问题1、从⊙O外一点P引⊙O的两条切
线,切点分别为A、B,如图是轴对称图形吗?那么线段PA和PB之间有何关系?
已知:PA、PB分别是⊙O的切线,点A、B分别为切点
求证:PA=PB
问题2:我们猜测的结果能否作为
定理来用呢?为了让我们得出的命
题成为定理,我们需要怎么做?
切线长定理:从圆外一点引圆的两条切线,它们的切线长相等.
1、情景问题 为了测量一个圆形锅盖的半径,某同学采用了如下办法:将锅盖平放在水平桌面上,用一个锐角为30°的三角板和一个刻度尺,按图中所示的方法得到相关数据,进而可求得锅盖的半径。若测得PA=5cm,则锅盖的半径长是多少?
P
A
B
O
四、运用新知,解决问题
问题2、如图,与三角形各边都相切的圆叫做三角形的内切圆,下图中存在切线长定理吗?
问题3:请同学们先在练习本上作
出已知⊙O的四条切线,如图9,
再互相交流与讨论四条切线围成的
四边形(即圆的外切四边形)有什么
性质,发现结论并试着加以说明。
圆的外切四边形对边的关系:
两组对边的和相等.
填空:如图,PA、PB分别与⊙O
相切于点A、B,求:
(1)若PB=12,PO=13,则AO= ( )
(2)若PO=10,AO=6,则PB= ( )
(3)若PA=4,AO=3,
则PO= ;
PD= ;
五、触类旁通,提升能力
已知:如图,Rt△ABC的两条直角边
AC=10,BC=24,⊙O 是△ABC 的内切
圆,切点分别为D,E,F,求⊙O 的半径.
六、课堂小结,畅谈收获
知识上:1、切线长的定义。
2、切线长定理。
3、圆外切四边形边的关系
方法上:观察—猜想—探索—验
证—证明。
情感上:独立思考,迎难而上,乐
于合作,自我评价。
七、推荐作业
A层:已知:如图,⊙O是△ABC的内
切圆,切点分别为D、E、F,
(1)图中共有几对相等线段?
(2)若AF=4,BD=6,CE=8,则
△ABC的周长是 ;
(3)若AB=9,BC=15,AC=12,则
AF= ,BD= ,CE= .
推荐作业
B层
1:已知,如图10,PA、PB分别与⊙O相切于点A、B,PO与⊙O相交于点D,且PA=4cm,PD=2cm.求半径OB的长
2.如图,PA、PB切⊙O于A、B,
PO交AB于E,等式
①AE=BE;②AO2=OE·OP;
③∠OAB=∠APB;
④PA=PB中,成立的有( )
A.1个 B.2个 C.3个 D.4个
教师寄语: 同学们! 请铭记: 勤奋是舟,规律是桨,只有刻苦努力,你们必将顺利抵港。
