北师大版七年级数学下册 2.1.3 垂线段及其性质 课件(31张PPT)
文档属性
| 名称 | 北师大版七年级数学下册 2.1.3 垂线段及其性质 课件(31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 624.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-03 14:26:07 | ||
图片预览










文档简介
第2课时 垂直
第二章 相交线与平行线
2.1 两条直线的位置关系
1.同一平面内两条直线的位置关系
2.对顶角的定义及其性质
3.余角、补角定义及其性质
4.邻补角定义及其性质
复
习
回
顾
1
知识点
垂直的定义
知识点
观察思考
当转动一木条的位置时,什么也随着发生了变化?
定义:在同一平面内,如果两条直线相交成直角,就说这两条直线互相垂直;其中一条直线叫做另一条直线的垂线,它们的交点O叫做垂足.如图.
垂足
垂 线
垂
线
垂足
垂 线
垂
线
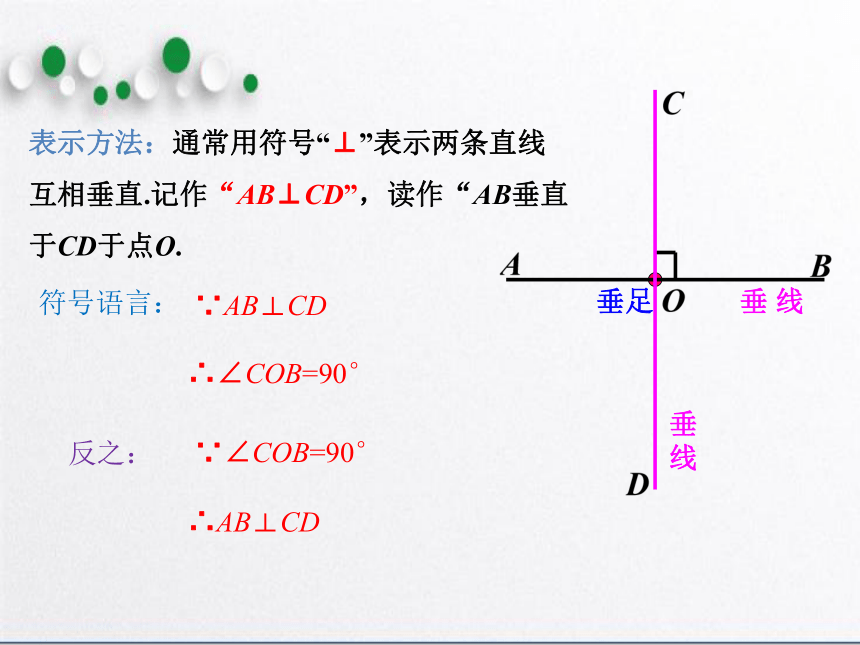
表示方法:通常用符号“⊥”表示两条直线互相垂直.记作“AB⊥CD”,读作“AB垂直于CD于点O.
符号语言:
∵AB⊥CD
∴∠COB=90°
反之:
∵∠COB=90°
∴AB⊥CD
问题:
(1)两条直线垂直和相交是什么关系?
(2)能否认为在同一平面内,两条直线的位置关系有3种:相交、平行、垂直?
垂直是相交的特殊情况 .
不能,在同一平面内,两条直线的位置关系只有
相交和平行两种 .
如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM.若∠AOM=35°,则∠CON的度数为( )
A.35°
B.45°
C.55°
D.65°
1
C
如图,CO⊥AB于点O,∠AOE=∠COF,则射
线OE,OF是什么位置关系?请说明理由.
解:射线OE,OF互相垂直.理由如下:
∵CO⊥AB,(已知)
∴∠AOC=90°.(垂直的定义)
∵∠AOE=∠COF,(已知)
∴∠AOE+∠COE=∠COF+∠COE,(等式的基本性质)
即∠AOC=∠EOF=90°.
∴OE与OF互相垂直. (垂直定义)
2
2
知识点
垂线的画法
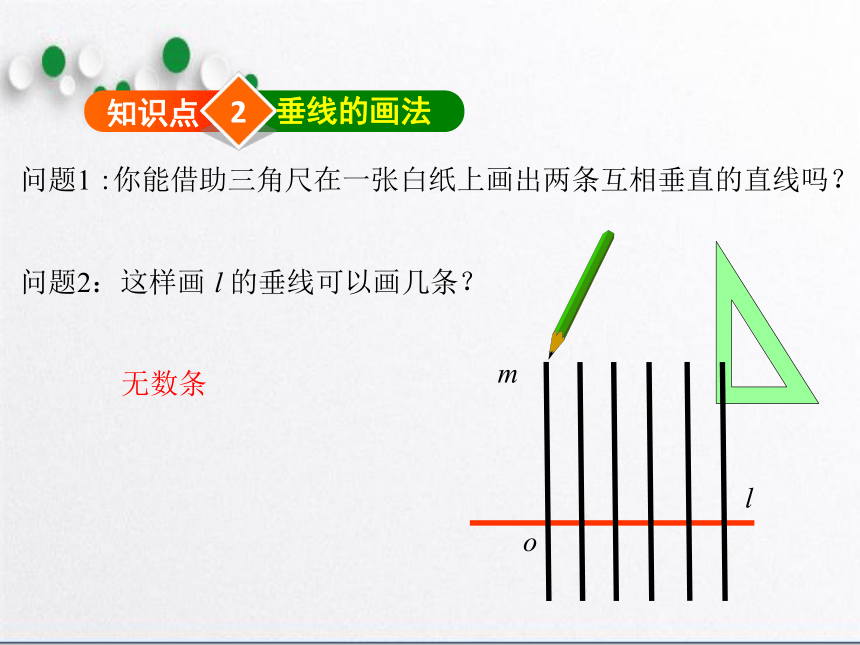
问题1 :你能借助三角尺在一张白纸上画出两条互相垂直的直线吗?
o
l
m
问题2:这样画 l 的垂线可以画几条?
无数条
问题3:(1)如图,已知直线 l 和l上的一点A ,过点A如何作l的垂线?
过直线上一点画已知直线的垂线,步骤如下:
A
.
l
(1)一靠:靠三角板,把三角板的 一直角边靠在直线上;
(2)二移:移动三角板到已知点;
(3)三画:沿着三角板的另一直角边
画出垂线.
m
则所画直线m是过点A的直线l的垂线.
(2)如图,已知直线 l 和l外的一点A,作l的垂线.
过直线外一点画已知直线的垂线,步骤如下:
l
.
A
B
(1)一靠:靠三角板,把三角板的 一直角边靠在直线上;
(2)二移:移动三角板到已知点;
(3)三画:沿着三角板的另一直角边
画出垂线,交直线l于B点.
则所画直线AB是过点A的直线l的垂线.
3
知识点
垂线的性质
想一想
(1)如图, 点A在直线l上,过点A画直线l的垂线,你能
画出多少 条?如果点A在直线l外呢?
∟
A
.
l
∟
. A
l
垂线的性质(一):
平面内,过一点有且只有一条直线与已知直线垂直.
归 纳
知3-导
如图,如果直线ON⊥直线a,直线OM⊥直线a,那么OM与ON重合(即O,M,N三点共线),其理由是( )
A.两点确定一条直线
B.在同一平面内,过两点有且只
有一条直线与已知直线垂直
C.在同一平面内,过一点有且只有一条直线与已
知直线垂直
D.两点之间,线段最短
知3-练
1
C
总 结
利用垂线的性质解答题目,要注意垂线性质满足的条件:
1. 在平面内;
2. 过一点,点的位置可以在直线上也可以在直线外;
3. 相交所成的角必须是直角.
以上三条缺一不可.
2
C
下列说法中,正确的有( )
①在平面内,过直线上一点有且只有一条直线垂直于已 知直线
②在平面内,过直线外一点有且只有一条直线垂直于已知直线
③在平面内,可以过任意一点画一条直线垂直于已知直线
④在平面内,有且只有一条直线垂直于已知直线
A.1个 B.2个 C.3个 D.4个
想一想
(2)如图,点P是直线 l 外一
点,PO⊥l,点O是垂足. 点A,B,C在直线l上,比较线段PO,PA,PB,PC的长短,你发现了什么?
直线外一点与直线上各点连接的所有线段中,垂线段最短.
P
A
B
C
l
D
简单说成:垂线段最短.
o
垂线段的定义:
过直线外一点画已知直线的垂线,这点与垂足之间的线段,
叫这点到已知直线的垂线段.
垂线的性质(二):
4
知识点
点到直线的距离
从直线外一点到这条直线所画垂线段的长度叫做这点到直线的距离.
A
B
下列说法正确的是( )
A.垂线段就是垂直于已知直线的线段
B.垂线段就是垂直于已知直线并且与已知直
线相交的线段
C.垂线段是一条竖起来的线段
D.过直线外一点向该直线作垂线,这一点到
垂足之间的线段叫垂线段
3
D
4 如图,三角形ABC中,∠C=90°,AC=3,点P
可以在直线BC上自由移动,则AP的长不可能是
( )
A.2.5 B.3 C.4 D.5
A
如图,在铁路旁有一李庄,现要建一火车站,为了使李庄人乘车最方便,请你在铁路线上选一点来建火车站,应建在( )
A.A点
B.B点
C.C点
D.D点
5
A
如图,AB是一条河流,要铺设管道将河水引到C,D
两个用水点,现有两种铺设管道的方案:
方案一:分别过点C,D作AB的
垂线,垂足分别为点E,F,沿
CE,DF铺设管道;
方案二:连接CD交AB于点P,
沿PC,PD铺设管道.
这两种铺设管道的方案哪一种更节省材料?为什么?
(河流的宽度可忽略不计)
6
要尽可能节省材料,也就是让管道的总长度更小.
方案一中CE,DF是垂线段,而方案二中PC,PD
不是垂线段,所以CE<PC,DF<PD.所以CE+DF
<PC+PD.所以方案一更节省材料.
导引:
按方案一铺设管道更节省材料.理由如下:
因为CE⊥AB,DF⊥AB,CD不垂直于AB,
且根据“垂线段最短”可知,CE<PC,DF<PD,
所以CE+DF<PC+PD.
所以沿CE,DF铺设管道更节省材料.
解:
本题主要利用“垂线段最短”来解决实际问题,
解决这类求最短距离问题时,要注意“垂线段最短”
与“两点之间,线段最短”的区别,辨明这两条性
质的应用条件:点到直线的最短距离,两点间的最
短距离.
总 结
如图所示,∠BAC=90°,AD⊥BC,垂足为D,则下面的结论中,正确的个数为( )
①AB与AC互相垂直;②AD与AC互相垂直;③点C到AB的垂线段是线段AB;④点A到BC的距离是线段AD;⑤线段AB的长度是点B到AC的距离;⑥线段AB是点B到BC的距离.
A.2 B.3
C.4 D.5
A
7
正确理解点到直线的距离及两点间的距离是解
决此类问题的关键.解决此类问题应注意:(1)点到
直线的距离是点到直线的垂线段的长度,而不是垂
线,也不是垂线段;(2)距离表示线段的长度,是一
个数量,与线段不能等同;(3)用垂线段的长度表示
点到直线的距离,其实质是点与垂足两点间的距离,
体现了数形结合思想.
总 结
如图,在三角形ABC中,∠ACB=90°,CD⊥AB,垂足为D.若AC=4 cm,BC=3 cm,AB=5 cm,则点A到直线BC的距离为________,点B到直线AC的距离为______,点C到直线AB的距离为______.
根据点到直线的距离的定义可知,
点A到直线BC的距离是线段AC的长,
点B到直线AC的距离是线段BC的长,点C到直线AB的距
离是线段CD的长.因为三角形ABC的面积S= AC·BC=
AB·CD,所以AC·BC=AB·CD,进而可得CD=2.4 cm.
导引:
4 cm
3 cm
2.4 cm
8
点P为直线m外一点,点A,B,C为直线m上三点,PA=4 cm,PB=5 cm,PC=2 cm,则点P到直线m的距离( )
A.等于4 cm B.等于2 cm
C.小于2 cm D.不大于2 cm
D
易错点:对垂线段的性质理解不透彻而致错.
9
错解:
B
诊断:
点到直线的距离是指这个点到直线的垂线段的长度.虽然垂线段最短,但是并没有说明PC是垂线段,所以垂线段的长度可能小于2 cm,也可能等于2 cm.
1.垂直的定义及其表示
2.垂线的画法:一靠二移三画
3.垂线的性质:
(一)平面内,过一点有且只有一条直线与已知直线垂直.
(二)直线外一点与直线上各点连接的所有线段中,垂线段最短.
4.点到直线的距离:直线外一点到这条直线的垂线段的长度, 叫做点到直线的距离.
第二章 相交线与平行线
2.1 两条直线的位置关系
1.同一平面内两条直线的位置关系
2.对顶角的定义及其性质
3.余角、补角定义及其性质
4.邻补角定义及其性质
复
习
回
顾
1
知识点
垂直的定义
知识点
观察思考
当转动一木条的位置时,什么也随着发生了变化?
定义:在同一平面内,如果两条直线相交成直角,就说这两条直线互相垂直;其中一条直线叫做另一条直线的垂线,它们的交点O叫做垂足.如图.
垂足
垂 线
垂
线
垂足
垂 线
垂
线
表示方法:通常用符号“⊥”表示两条直线互相垂直.记作“AB⊥CD”,读作“AB垂直于CD于点O.
符号语言:
∵AB⊥CD
∴∠COB=90°
反之:
∵∠COB=90°
∴AB⊥CD
问题:
(1)两条直线垂直和相交是什么关系?
(2)能否认为在同一平面内,两条直线的位置关系有3种:相交、平行、垂直?
垂直是相交的特殊情况 .
不能,在同一平面内,两条直线的位置关系只有
相交和平行两种 .
如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM.若∠AOM=35°,则∠CON的度数为( )
A.35°
B.45°
C.55°
D.65°
1
C
如图,CO⊥AB于点O,∠AOE=∠COF,则射
线OE,OF是什么位置关系?请说明理由.
解:射线OE,OF互相垂直.理由如下:
∵CO⊥AB,(已知)
∴∠AOC=90°.(垂直的定义)
∵∠AOE=∠COF,(已知)
∴∠AOE+∠COE=∠COF+∠COE,(等式的基本性质)
即∠AOC=∠EOF=90°.
∴OE与OF互相垂直. (垂直定义)
2
2
知识点
垂线的画法
问题1 :你能借助三角尺在一张白纸上画出两条互相垂直的直线吗?
o
l
m
问题2:这样画 l 的垂线可以画几条?
无数条
问题3:(1)如图,已知直线 l 和l上的一点A ,过点A如何作l的垂线?
过直线上一点画已知直线的垂线,步骤如下:
A
.
l
(1)一靠:靠三角板,把三角板的 一直角边靠在直线上;
(2)二移:移动三角板到已知点;
(3)三画:沿着三角板的另一直角边
画出垂线.
m
则所画直线m是过点A的直线l的垂线.
(2)如图,已知直线 l 和l外的一点A,作l的垂线.
过直线外一点画已知直线的垂线,步骤如下:
l
.
A
B
(1)一靠:靠三角板,把三角板的 一直角边靠在直线上;
(2)二移:移动三角板到已知点;
(3)三画:沿着三角板的另一直角边
画出垂线,交直线l于B点.
则所画直线AB是过点A的直线l的垂线.
3
知识点
垂线的性质
想一想
(1)如图, 点A在直线l上,过点A画直线l的垂线,你能
画出多少 条?如果点A在直线l外呢?
∟
A
.
l
∟
. A
l
垂线的性质(一):
平面内,过一点有且只有一条直线与已知直线垂直.
归 纳
知3-导
如图,如果直线ON⊥直线a,直线OM⊥直线a,那么OM与ON重合(即O,M,N三点共线),其理由是( )
A.两点确定一条直线
B.在同一平面内,过两点有且只
有一条直线与已知直线垂直
C.在同一平面内,过一点有且只有一条直线与已
知直线垂直
D.两点之间,线段最短
知3-练
1
C
总 结
利用垂线的性质解答题目,要注意垂线性质满足的条件:
1. 在平面内;
2. 过一点,点的位置可以在直线上也可以在直线外;
3. 相交所成的角必须是直角.
以上三条缺一不可.
2
C
下列说法中,正确的有( )
①在平面内,过直线上一点有且只有一条直线垂直于已 知直线
②在平面内,过直线外一点有且只有一条直线垂直于已知直线
③在平面内,可以过任意一点画一条直线垂直于已知直线
④在平面内,有且只有一条直线垂直于已知直线
A.1个 B.2个 C.3个 D.4个
想一想
(2)如图,点P是直线 l 外一
点,PO⊥l,点O是垂足. 点A,B,C在直线l上,比较线段PO,PA,PB,PC的长短,你发现了什么?
直线外一点与直线上各点连接的所有线段中,垂线段最短.
P
A
B
C
l
D
简单说成:垂线段最短.
o
垂线段的定义:
过直线外一点画已知直线的垂线,这点与垂足之间的线段,
叫这点到已知直线的垂线段.
垂线的性质(二):
4
知识点
点到直线的距离
从直线外一点到这条直线所画垂线段的长度叫做这点到直线的距离.
A
B
下列说法正确的是( )
A.垂线段就是垂直于已知直线的线段
B.垂线段就是垂直于已知直线并且与已知直
线相交的线段
C.垂线段是一条竖起来的线段
D.过直线外一点向该直线作垂线,这一点到
垂足之间的线段叫垂线段
3
D
4 如图,三角形ABC中,∠C=90°,AC=3,点P
可以在直线BC上自由移动,则AP的长不可能是
( )
A.2.5 B.3 C.4 D.5
A
如图,在铁路旁有一李庄,现要建一火车站,为了使李庄人乘车最方便,请你在铁路线上选一点来建火车站,应建在( )
A.A点
B.B点
C.C点
D.D点
5
A
如图,AB是一条河流,要铺设管道将河水引到C,D
两个用水点,现有两种铺设管道的方案:
方案一:分别过点C,D作AB的
垂线,垂足分别为点E,F,沿
CE,DF铺设管道;
方案二:连接CD交AB于点P,
沿PC,PD铺设管道.
这两种铺设管道的方案哪一种更节省材料?为什么?
(河流的宽度可忽略不计)
6
要尽可能节省材料,也就是让管道的总长度更小.
方案一中CE,DF是垂线段,而方案二中PC,PD
不是垂线段,所以CE<PC,DF<PD.所以CE+DF
<PC+PD.所以方案一更节省材料.
导引:
按方案一铺设管道更节省材料.理由如下:
因为CE⊥AB,DF⊥AB,CD不垂直于AB,
且根据“垂线段最短”可知,CE<PC,DF<PD,
所以CE+DF<PC+PD.
所以沿CE,DF铺设管道更节省材料.
解:
本题主要利用“垂线段最短”来解决实际问题,
解决这类求最短距离问题时,要注意“垂线段最短”
与“两点之间,线段最短”的区别,辨明这两条性
质的应用条件:点到直线的最短距离,两点间的最
短距离.
总 结
如图所示,∠BAC=90°,AD⊥BC,垂足为D,则下面的结论中,正确的个数为( )
①AB与AC互相垂直;②AD与AC互相垂直;③点C到AB的垂线段是线段AB;④点A到BC的距离是线段AD;⑤线段AB的长度是点B到AC的距离;⑥线段AB是点B到BC的距离.
A.2 B.3
C.4 D.5
A
7
正确理解点到直线的距离及两点间的距离是解
决此类问题的关键.解决此类问题应注意:(1)点到
直线的距离是点到直线的垂线段的长度,而不是垂
线,也不是垂线段;(2)距离表示线段的长度,是一
个数量,与线段不能等同;(3)用垂线段的长度表示
点到直线的距离,其实质是点与垂足两点间的距离,
体现了数形结合思想.
总 结
如图,在三角形ABC中,∠ACB=90°,CD⊥AB,垂足为D.若AC=4 cm,BC=3 cm,AB=5 cm,则点A到直线BC的距离为________,点B到直线AC的距离为______,点C到直线AB的距离为______.
根据点到直线的距离的定义可知,
点A到直线BC的距离是线段AC的长,
点B到直线AC的距离是线段BC的长,点C到直线AB的距
离是线段CD的长.因为三角形ABC的面积S= AC·BC=
AB·CD,所以AC·BC=AB·CD,进而可得CD=2.4 cm.
导引:
4 cm
3 cm
2.4 cm
8
点P为直线m外一点,点A,B,C为直线m上三点,PA=4 cm,PB=5 cm,PC=2 cm,则点P到直线m的距离( )
A.等于4 cm B.等于2 cm
C.小于2 cm D.不大于2 cm
D
易错点:对垂线段的性质理解不透彻而致错.
9
错解:
B
诊断:
点到直线的距离是指这个点到直线的垂线段的长度.虽然垂线段最短,但是并没有说明PC是垂线段,所以垂线段的长度可能小于2 cm,也可能等于2 cm.
1.垂直的定义及其表示
2.垂线的画法:一靠二移三画
3.垂线的性质:
(一)平面内,过一点有且只有一条直线与已知直线垂直.
(二)直线外一点与直线上各点连接的所有线段中,垂线段最短.
4.点到直线的距离:直线外一点到这条直线的垂线段的长度, 叫做点到直线的距离.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
