北师大版七年级数学下册 3.3. 用图象表示的变量间关系 (共24张PPT)
文档属性
| 名称 | 北师大版七年级数学下册 3.3. 用图象表示的变量间关系 (共24张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-03 14:27:30 | ||
图片预览





文档简介
第三章 变量之间的关系
3.3 用图象表示的变量间关系
课堂讲解
用曲线型图象表示两个变量间关系
用折线型图象表示变量间的关系
从折线型图象中读取变量间关系信息
表示变量间的关系的方法有哪些?
复
习
回
顾
表格法,关系式法
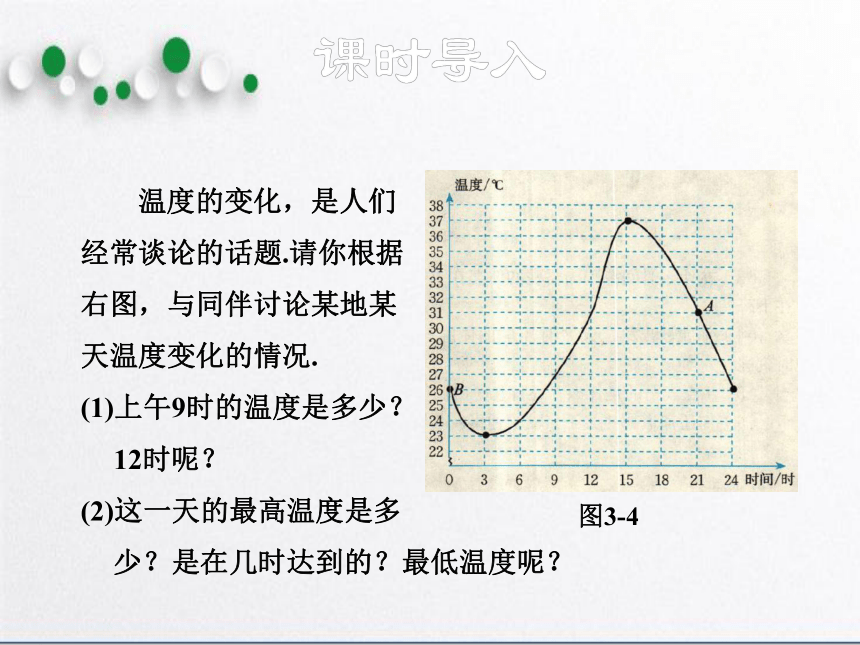
温度的变化,是人们
经常谈论的话题.请你根据
右图,与同伴讨论某地某
天温度变化的情况.
(1)上午9时的温度是多少?
12时呢?
(2)这一天的最高温度是多
少?是在几时达到的?最低温度呢?
图3-4
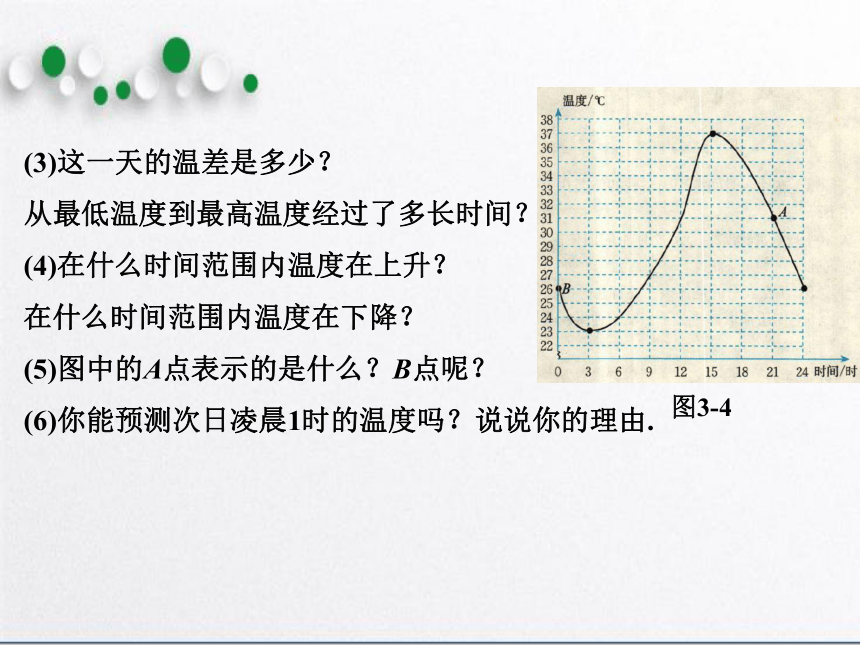
(3)这一天的温差是多少?
从最低温度到最高温度经过了多长时间?
(4)在什么时间范围内温度在上升?
在什么时间范围内温度在下降?
(5)图中的A点表示的是什么?B点呢?
(6)你能预测次日凌晨1时的温度吗?说说你的理由.
图3-4
图3-4表示了温度随时间的变化而变化的情况,
它是温度与时间之间关系的图象.图象是我们表示变
量之间关系的又一种方法,它的特点是非常直观.
在用图象表示变量之间的关系时,通常用水平
方向的数轴(称为横轴)上的点表示自变量,用竖直方
向的数轴(称为纵轴)上的点表示因变量.
归 纳
课本69页议一议上面,找出并标注出来
1
知识点
用曲线型图象表示两个变量间关系
议一议
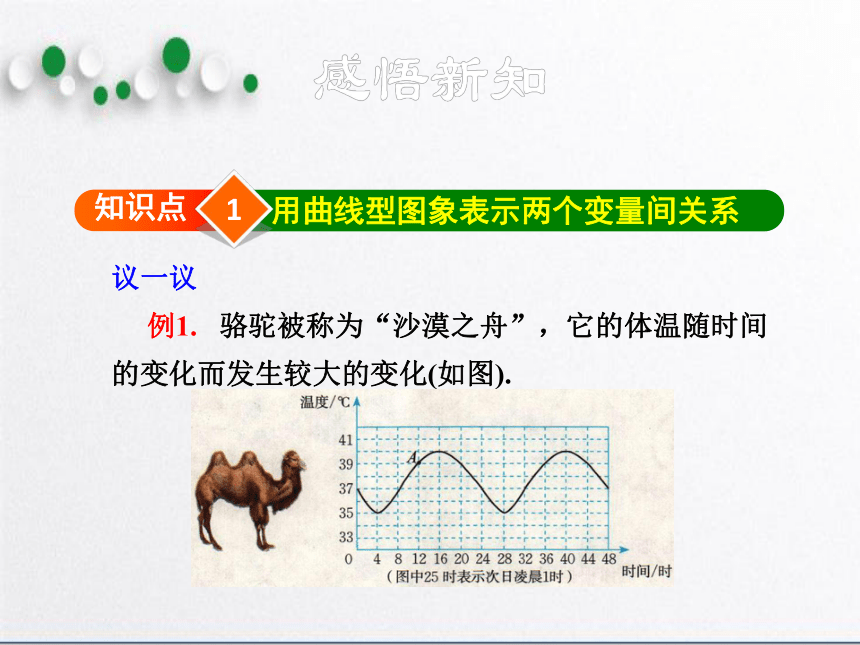
例1. 骆驼被称为“沙漠之舟”,它的体温随时间的变化而发生较大的变化(如图).
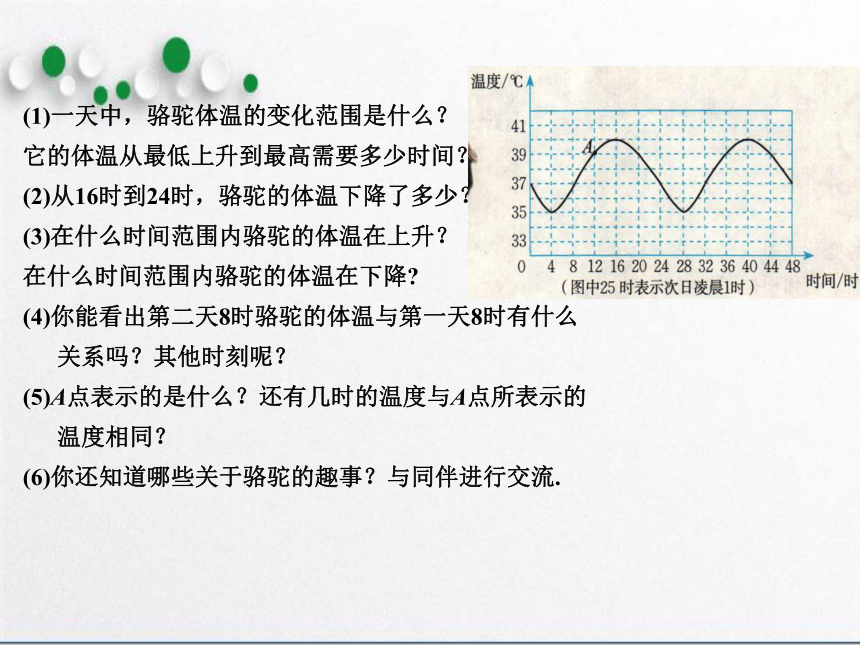
(1)一天中,骆驼体温的变化范围是什么?
它的体温从最低上升到最高需要多少时间?
(2)从16时到24时,骆驼的体温下降了多少?
(3)在什么时间范围内骆驼的体温在上升?
在什么时间范围内骆驼的体温在下降?
(4)你能看出第二天8时骆驼的体温与第一天8时有什么
关系吗?其他时刻呢?
(5)A点表示的是什么?还有几时的温度与A点所表示的
温度相同?
(6)你还知道哪些关于骆驼的趣事?与同伴进行交流.
注意:对图象进行水平方向左右的比较、竖直方向高低的比较.水平方向的左右比较反映了自变量值的大小变化,右边大于左边;竖直方向的高低比较反映了因变量值的大小变化,高者大于低者.
总 结
2
知识点
用折线型图象表示变量间的关系
每一辆汽车上都有一个时速表用来指示汽车当
时的速度. 你知道现在汽车的速度是多少吗?
汽车在行驶的过程中,速度往往是变化的.下图表
示一辆汽车的速度随时间变化而变化的情况.
(1)汽车从出发到最后停止
共经过了多少时间?
它的最高时速是多少?
(2)汽车在哪些时间段保持
匀速行驶?时速分别是多少?
(3)出发后8分到10分之间可能发生了什么情况?
(4)用自己的语言大致描述这辆汽车的行驶情况.
注意:在一个变化过程中,两个变量之间的关系不
是一成不变的,有时随着自变量的变化,因变量与
自变量之间的关系也会发生变化,反映在图象上就
是分段图象.
例2
下图的图象反映的过程是:小明从家去超市买文具,又去书店购书,然后回家.其中x(min)表示时间,y(km)表示小明离家的距离,小明家、超市、书店在同一条直线上.根据图象回答下列问题.
(1)超市离小明家有多远?
小明走到超市用了多少时间?
(2)超市离书店有多远?小明在
书店购书用了多少时间?
(3)书店离小明家有多远?小明从书店走回家的平均速
度是每分钟多少米?
读懂分段图象所表示的实际意义是解决本题的关键.
导引:
解:
(1)由图象可以看出超市离小明家1.1 km,
小明走到超市用了15 min.
(2)超市离书店2-1.1=0.9(km),
小明在书店购书用了55-37=18(min).
(3)由图象可以看出书店离小明家2 km,
小明从书店走回家的平均速度是
运用数形结合思想解答此题.图象上任意一
点都对应了一个自变量的值和一个因变量的值.
总 结
练习1
【中考·凉山州】小明和哥哥从家里出发去买书,从家出发走了20 min到一个离家1 000 m的书店,小明买了书后随即按原路返回;哥哥看了20 min书后,用15 min返回家.
下面的图象中哪
一个表示哥哥离
家时间与距离之
间的关系( )
D
3
知识点
从图象中读取变量间关系信息
根据图象读取信息时要把握四个方面:
(1)横轴和纵轴的意义.
(2)对于某个具体点,可向横、纵轴作垂线,从而求得具体的值;
(3)在实际问题中,要注意图象与横、纵轴的交点代表的实际意义.
(4)注意图像中的拐点,是从一个变化过程到另一个变化过程的转折点.(特别是在几何图形中的动点问题)
例3
某年初,我国西南部分省市遭遇了
严重干旱.某水库的蓄水量随着时
间的增加而减小,干旱持续时间 t
(天)与蓄水量V(万立方米)的变化情
况如图,根据图象回答问题:
(1)这个图象反映了哪两个变量之间的关系?
(2)根据图象填表:
(3)当t取0至60天之间的任一值时,对应几个V值?
(4)写出V和t之间的关系式?
干旱持续时间t/天
0
10
20
30
40
50
60
蓄水量V/万立方米
?
?
?
?
?
?
?
(1)图象反映了干旱持续时间与水库蓄水量之间的关系.
(2)填表如下:
(3)当t取0至60天之间的任一值时,对应着一个V值.
(4)根据图象可知,该水库初始蓄水量为1 200万立方米,
干旱每持续10天,蓄水量相应减少200万立方米,
所以V和t之间的关系式为
V=1 200- =-20t+1 200(0≤t≤60).
解:
干旱持续时间t/天
0
10
20
30
40
50
60
蓄水量V/万立方米
1 200
1 000
800
600
400
200
0
本例通过“形”,即图象中的信息,用列表及关
系式这个“数”来表示说明,三种表示方法之间有互
补性,是可以相互转化的,体现了数形结合思想的应
用.
总 结
例4
.如图①,在长方形ABCD中,动点E从点B出发,沿B→A→D→C方向运动至点C处停止,设点E运动的路程为x,三角形BCE的面积为y,如果y关于x的变化关系图象如图②,则当x=7时,点E应运动到( )
A.点C处
B.点D处
C.点B处
D.点A处
B
x是自变量,y是因变量,点E在运动的过程中,三角形
BCE的底边BC不变,而BC边上的高有时在变化,当点E
在AB上运动时,BC边上的高变得越来越大,此时三角形
BCE的面积不断增大;当点E在AD上运动时,BC边上的
高不变,此时三角形BCE的面积不变;当点E在DC上运
动时,BC边上的高不断减小,此时三角形BCE的面积不
断减小.观察图②,可知当x=7时,所对应的点正处于
水平线段与下降线段的交界处,即点E应运动到面积不发
生变化,若继续运动,面积随着变小的地方.结合图①,
可知点E运动到了点D处.
导引:
运用数形结合思想来解答,认真观察图形与图象,
仔细分析问题情境中的变量间的变化关系与图象的对
应关系,特别要注意抓住关键点.
总 结
其特点是直观
变量之间的关系
表格法
关系式法
图象法
是从“数”的角度反
映变量之间的关系:
其特点是清楚
是从“式”的角度反
映变量之间的关系:
其特点是简单明了
是从“形”的角度反
映变量之间的关系:
1
知识小结
3.3 用图象表示的变量间关系
课堂讲解
用曲线型图象表示两个变量间关系
用折线型图象表示变量间的关系
从折线型图象中读取变量间关系信息
表示变量间的关系的方法有哪些?
复
习
回
顾
表格法,关系式法
温度的变化,是人们
经常谈论的话题.请你根据
右图,与同伴讨论某地某
天温度变化的情况.
(1)上午9时的温度是多少?
12时呢?
(2)这一天的最高温度是多
少?是在几时达到的?最低温度呢?
图3-4
(3)这一天的温差是多少?
从最低温度到最高温度经过了多长时间?
(4)在什么时间范围内温度在上升?
在什么时间范围内温度在下降?
(5)图中的A点表示的是什么?B点呢?
(6)你能预测次日凌晨1时的温度吗?说说你的理由.
图3-4
图3-4表示了温度随时间的变化而变化的情况,
它是温度与时间之间关系的图象.图象是我们表示变
量之间关系的又一种方法,它的特点是非常直观.
在用图象表示变量之间的关系时,通常用水平
方向的数轴(称为横轴)上的点表示自变量,用竖直方
向的数轴(称为纵轴)上的点表示因变量.
归 纳
课本69页议一议上面,找出并标注出来
1
知识点
用曲线型图象表示两个变量间关系
议一议
例1. 骆驼被称为“沙漠之舟”,它的体温随时间的变化而发生较大的变化(如图).
(1)一天中,骆驼体温的变化范围是什么?
它的体温从最低上升到最高需要多少时间?
(2)从16时到24时,骆驼的体温下降了多少?
(3)在什么时间范围内骆驼的体温在上升?
在什么时间范围内骆驼的体温在下降?
(4)你能看出第二天8时骆驼的体温与第一天8时有什么
关系吗?其他时刻呢?
(5)A点表示的是什么?还有几时的温度与A点所表示的
温度相同?
(6)你还知道哪些关于骆驼的趣事?与同伴进行交流.
注意:对图象进行水平方向左右的比较、竖直方向高低的比较.水平方向的左右比较反映了自变量值的大小变化,右边大于左边;竖直方向的高低比较反映了因变量值的大小变化,高者大于低者.
总 结
2
知识点
用折线型图象表示变量间的关系
每一辆汽车上都有一个时速表用来指示汽车当
时的速度. 你知道现在汽车的速度是多少吗?
汽车在行驶的过程中,速度往往是变化的.下图表
示一辆汽车的速度随时间变化而变化的情况.
(1)汽车从出发到最后停止
共经过了多少时间?
它的最高时速是多少?
(2)汽车在哪些时间段保持
匀速行驶?时速分别是多少?
(3)出发后8分到10分之间可能发生了什么情况?
(4)用自己的语言大致描述这辆汽车的行驶情况.
注意:在一个变化过程中,两个变量之间的关系不
是一成不变的,有时随着自变量的变化,因变量与
自变量之间的关系也会发生变化,反映在图象上就
是分段图象.
例2
下图的图象反映的过程是:小明从家去超市买文具,又去书店购书,然后回家.其中x(min)表示时间,y(km)表示小明离家的距离,小明家、超市、书店在同一条直线上.根据图象回答下列问题.
(1)超市离小明家有多远?
小明走到超市用了多少时间?
(2)超市离书店有多远?小明在
书店购书用了多少时间?
(3)书店离小明家有多远?小明从书店走回家的平均速
度是每分钟多少米?
读懂分段图象所表示的实际意义是解决本题的关键.
导引:
解:
(1)由图象可以看出超市离小明家1.1 km,
小明走到超市用了15 min.
(2)超市离书店2-1.1=0.9(km),
小明在书店购书用了55-37=18(min).
(3)由图象可以看出书店离小明家2 km,
小明从书店走回家的平均速度是
运用数形结合思想解答此题.图象上任意一
点都对应了一个自变量的值和一个因变量的值.
总 结
练习1
【中考·凉山州】小明和哥哥从家里出发去买书,从家出发走了20 min到一个离家1 000 m的书店,小明买了书后随即按原路返回;哥哥看了20 min书后,用15 min返回家.
下面的图象中哪
一个表示哥哥离
家时间与距离之
间的关系( )
D
3
知识点
从图象中读取变量间关系信息
根据图象读取信息时要把握四个方面:
(1)横轴和纵轴的意义.
(2)对于某个具体点,可向横、纵轴作垂线,从而求得具体的值;
(3)在实际问题中,要注意图象与横、纵轴的交点代表的实际意义.
(4)注意图像中的拐点,是从一个变化过程到另一个变化过程的转折点.(特别是在几何图形中的动点问题)
例3
某年初,我国西南部分省市遭遇了
严重干旱.某水库的蓄水量随着时
间的增加而减小,干旱持续时间 t
(天)与蓄水量V(万立方米)的变化情
况如图,根据图象回答问题:
(1)这个图象反映了哪两个变量之间的关系?
(2)根据图象填表:
(3)当t取0至60天之间的任一值时,对应几个V值?
(4)写出V和t之间的关系式?
干旱持续时间t/天
0
10
20
30
40
50
60
蓄水量V/万立方米
?
?
?
?
?
?
?
(1)图象反映了干旱持续时间与水库蓄水量之间的关系.
(2)填表如下:
(3)当t取0至60天之间的任一值时,对应着一个V值.
(4)根据图象可知,该水库初始蓄水量为1 200万立方米,
干旱每持续10天,蓄水量相应减少200万立方米,
所以V和t之间的关系式为
V=1 200- =-20t+1 200(0≤t≤60).
解:
干旱持续时间t/天
0
10
20
30
40
50
60
蓄水量V/万立方米
1 200
1 000
800
600
400
200
0
本例通过“形”,即图象中的信息,用列表及关
系式这个“数”来表示说明,三种表示方法之间有互
补性,是可以相互转化的,体现了数形结合思想的应
用.
总 结
例4
.如图①,在长方形ABCD中,动点E从点B出发,沿B→A→D→C方向运动至点C处停止,设点E运动的路程为x,三角形BCE的面积为y,如果y关于x的变化关系图象如图②,则当x=7时,点E应运动到( )
A.点C处
B.点D处
C.点B处
D.点A处
B
x是自变量,y是因变量,点E在运动的过程中,三角形
BCE的底边BC不变,而BC边上的高有时在变化,当点E
在AB上运动时,BC边上的高变得越来越大,此时三角形
BCE的面积不断增大;当点E在AD上运动时,BC边上的
高不变,此时三角形BCE的面积不变;当点E在DC上运
动时,BC边上的高不断减小,此时三角形BCE的面积不
断减小.观察图②,可知当x=7时,所对应的点正处于
水平线段与下降线段的交界处,即点E应运动到面积不发
生变化,若继续运动,面积随着变小的地方.结合图①,
可知点E运动到了点D处.
导引:
运用数形结合思想来解答,认真观察图形与图象,
仔细分析问题情境中的变量间的变化关系与图象的对
应关系,特别要注意抓住关键点.
总 结
其特点是直观
变量之间的关系
表格法
关系式法
图象法
是从“数”的角度反
映变量之间的关系:
其特点是清楚
是从“式”的角度反
映变量之间的关系:
其特点是简单明了
是从“形”的角度反
映变量之间的关系:
1
知识小结
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
