北师大版七年级数学下册 第5章 第2节 探索轴对称的性质 (1) 课件(共23张PPT)
文档属性
| 名称 | 北师大版七年级数学下册 第5章 第2节 探索轴对称的性质 (1) 课件(共23张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 715.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-03 14:40:17 | ||
图片预览




文档简介
(共23张PPT)
XX幼儿园园长工作计划报告
以为指导,以总校目标作为指导方针,以爱为教育的基础,结合本园实际,继续以“我能行,我努力,我真棒!”为精神动力,抓好常规工作的同时,继续建设本园特色,使教育质量上一个新台阶。让我园成为孩子的乐园,家长的放心园,老师的收获园。
二、关键词:坚持反思感恩
、把责任文化打造成部门文化的根基。
1、以“责任”为主题,以“责任”为根基,倡导老师多读书,组织老师们以某本书为中心,在读书中体会生活,学会工作,从而学会感恩,在感恩中提高工作效率,提高幸福指数。
2、每周例会智慧分享,行政和组长把一些“事实性反馈”给老师,使老师做事有的放矢。每周由一位老师把自己收获的一些感受分享给大家。从而把积极、上进、健康的思想带给大家。
3、周二保育员例会,在上个学期的收获中,鼓励保育员在每周例会中和大家分享“我在班级管理中学到了什么”进一步提升“教”的能力!
、在文化背景的引导下,在反思中,坚持我们的收获,努力提高“品质”。
1、教研活动:教师研讨课严格按照我们“流程”进行,资料积累到位,一学期中每位教师要求自己上一节“好课。”
2、年级组工作:常规性的幼儿活动以年级组为单位展开,本学
5.2 探索轴对称的性质
复习回顾
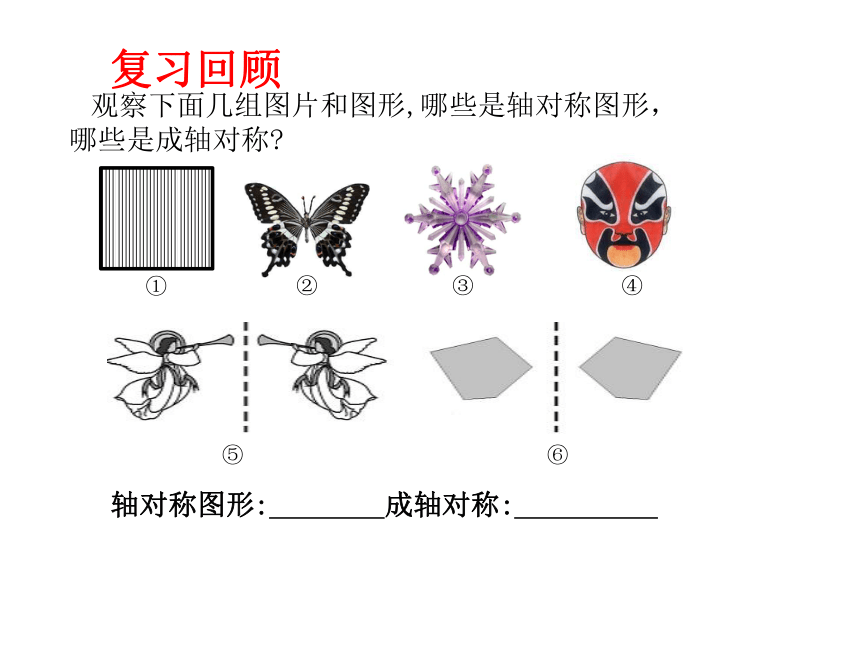
观察下面几组图片和图形,哪些是轴对称图形,哪些是成轴对称
轴对称图形: 成轴对称:
①
②
③
④
⑤
⑥
A
B
C
A/
B/
C/
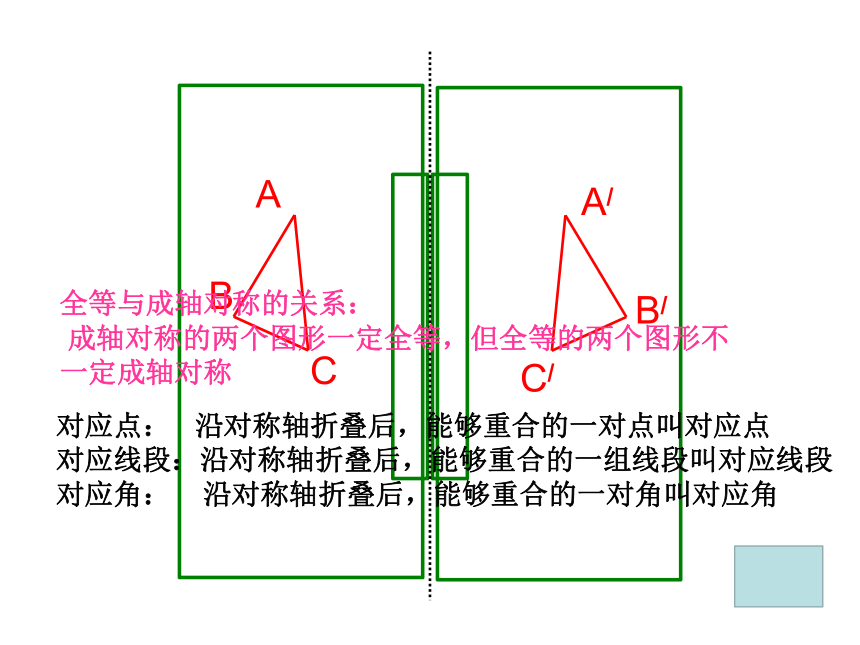
全等与成轴对称的关系:
成轴对称的两个图形一定全等,但全等的两个图形不一定成轴对称
对应点: 沿对称轴折叠后,能够重合的一对点叫对应点
对应线段:沿对称轴折叠后,能够重合的一组线段叫对应线段
对应角: 沿对称轴折叠后,能够重合的一对角叫对应角
扎字实验
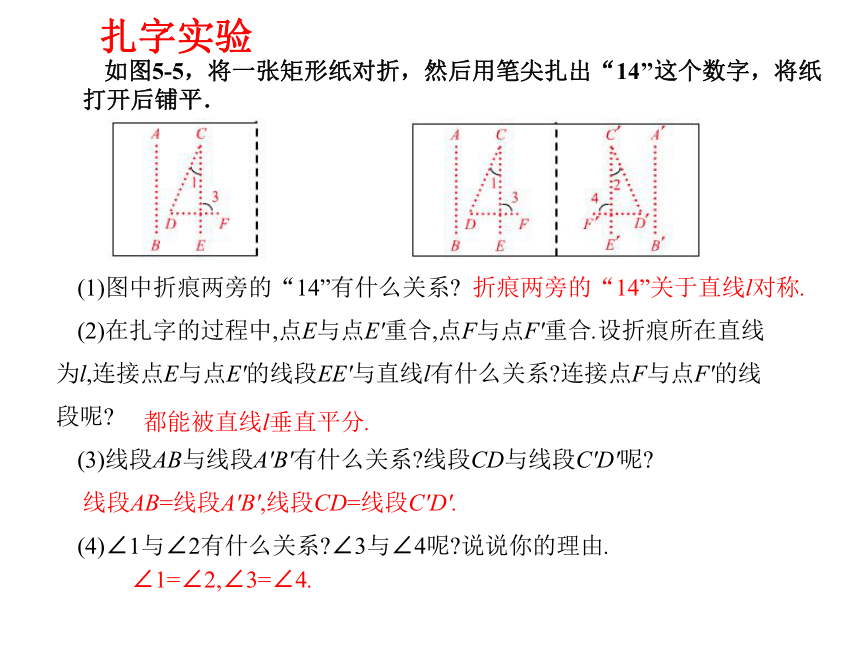
如图5-5,将一张矩形纸对折,然后用笔尖扎出“14’’这个数字,将纸打开后铺平.
(1)图中折痕两旁的“14”有什么关系
(2)在扎字的过程中,点E与点E'重合,点F与点F'重合.设折痕所在直线为l,连接点E与点E'的线段EE'与直线l有什么关系 连接点F与点F'的线段呢
(3)线段AB与线段A'B'有什么关系 线段CD与线段C'D'呢
(4)∠1与∠2有什么关系 ∠3与∠4呢 说说你的理由.
∠1=∠2,∠3=∠4.
折痕两旁的“14”关于直线l对称.
都能被直线l垂直平分.
线段AB=线段A'B',线段CD=线段C'D'.
A
B
C
D
D1
C1
A1
B1
3
4
1
2
做一做:
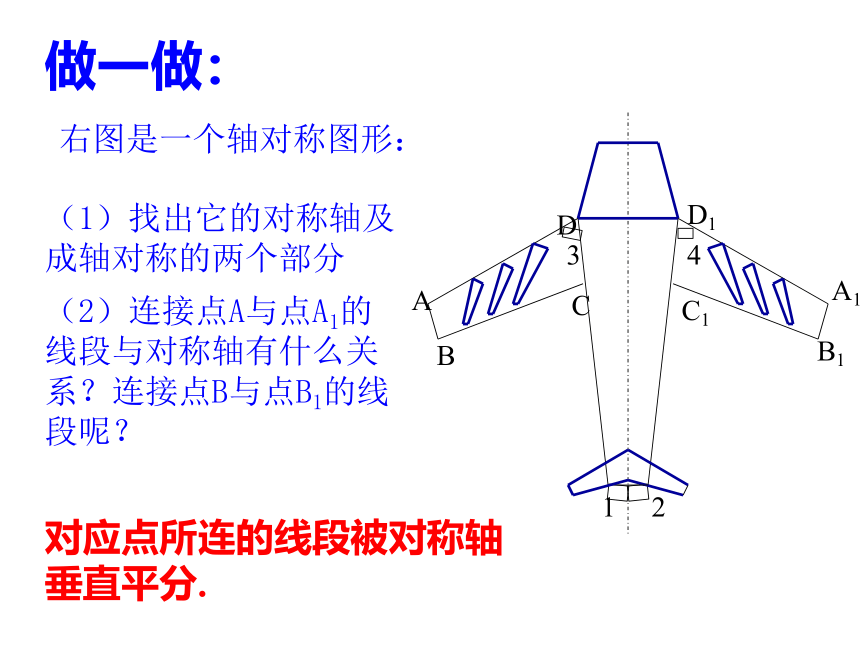
右图是一个轴对称图形:
(1)找出它的对称轴及成轴对称的两个部分
(2)连接点A与点A1的线段与对称轴有什么关系?连接点B与点B1的线段呢?
对应点所连的线段被对称轴垂直平分.
A
B
C
D
D1
C1
A1
B1
3
4
1
2
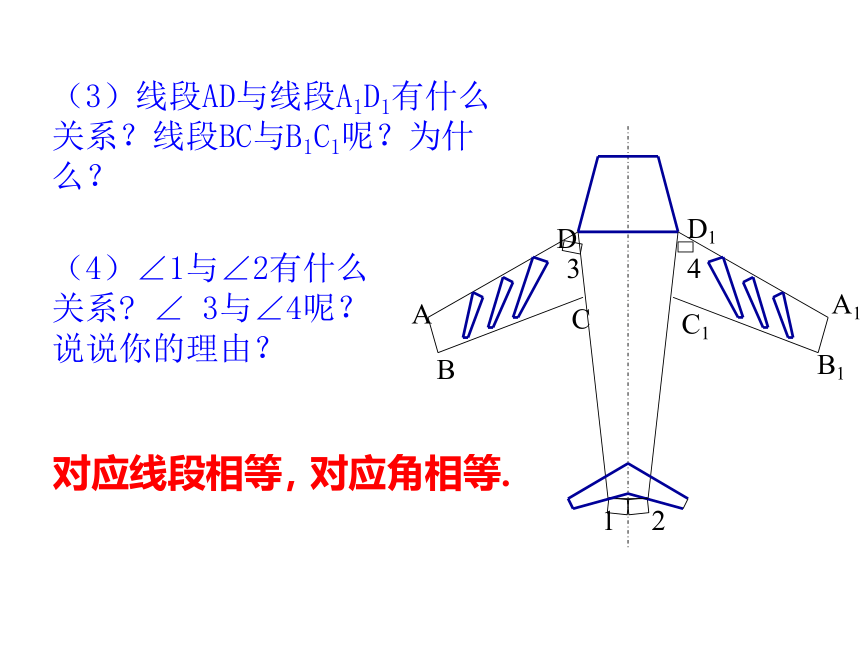
(3)线段AD与线段A1D1有什么关系?线段BC与B1C1呢?为什么?
(4)∠1与∠2有什么关系 ∠ 3与∠4呢?说说你的理由?
对应角相等.
对应线段相等,
在轴对称图形或两个成轴对称的图形中:
1.对应点所连的线段被对称轴垂直平分
2.对应线段相等
3.对应角相等
根据轴对称的性质进行一次实战演习
轴对称性质的应用
(1)给你一个点A,你能找到并画出点A关于直线l的对应点A'吗 你是如何做的 与同伴交流.
如图所示,①过A点画AO⊥l于O点;
②延长AO到点A'使OA'=AO.
所以点A'就是点A关于直线l的对应点.
若两点所连线段被某直线垂直平分,则此直线为这两点的对称轴;
O
A'
(2)同学们能够画出一个点的对称点,那么如果老师给的是一条线段呢 如图,画出线段AB关于直线l成轴对称的线段A'B'.
A'
B'.
3. 画出△ABC关于直线l的对称图形.
解:如图所示.
方法总结:先确定一些关键的点(线段端点,三角形的顶点),然后作这些关键点的对称点,连接这些对称点即可.
1.如果两个图形关于某条直线对称,那么对应点所
连的线段被__________垂直平分.
2.下图是轴对称图形,相等的线段是____________
________,相等的角是__________.
A
B
C
D
E
对称轴
AB=CD,
BE=CE
∠B=∠C
当堂练习
3.两个图形关于某直线对称,对称点一定 ( ) A.这直线的两旁 B.这直线的同旁
C.这直线上 D.这直线两旁或这直线上
D
4.轴对称图形沿对称轴对折后,对称轴两旁的
部分( )
A.完全重合 B.不完全重合
C.两者都有
A
实战演练
5.如图,△ABC与△A1B1C1关于直线l对称,则∠B
为______.
解析:由轴对称的性质可得∠A1=∠A=50°, ∠C=∠C1=30°,所以∠B=∠B1=180°-50°-30°=100°.
100°
后面还有智力测验,你想试一试吗?
1. 一个汽车车牌在水中的倒影如图所示,你能确定该车的牌照号码吗?
你的眼力
下面哪一面镜子里是他像?
( D )
3、一次晚会上,主持人出了一道题目:“如何把 变成一个真正的等式?”过了很长时间,也没有人答出。
小兰仅仅拿了一面镜子,就很快解决了这道题目。
你知道她是怎样做的吗?
你知道为什么吗?
如图,宿州市要修建两个水上公园A,B,要在新汴河边修建一个水泵站向A,B两地送水,修在什么地方所用的水管最短?
A
B
实战演练
A
′
.
.
.
P
O
本节课学习了_________
学会了_________
感受了_________
作业
基础性作业:
画一个轴对称图形,并标明对称轴;
感谢语:
谢谢各位老师的光临!感谢大家的支持!
您的鼓励是我前进的动力!
再见!
XX幼儿园园长工作计划报告
以为指导,以总校目标作为指导方针,以爱为教育的基础,结合本园实际,继续以“我能行,我努力,我真棒!”为精神动力,抓好常规工作的同时,继续建设本园特色,使教育质量上一个新台阶。让我园成为孩子的乐园,家长的放心园,老师的收获园。
二、关键词:坚持反思感恩
、把责任文化打造成部门文化的根基。
1、以“责任”为主题,以“责任”为根基,倡导老师多读书,组织老师们以某本书为中心,在读书中体会生活,学会工作,从而学会感恩,在感恩中提高工作效率,提高幸福指数。
2、每周例会智慧分享,行政和组长把一些“事实性反馈”给老师,使老师做事有的放矢。每周由一位老师把自己收获的一些感受分享给大家。从而把积极、上进、健康的思想带给大家。
3、周二保育员例会,在上个学期的收获中,鼓励保育员在每周例会中和大家分享“我在班级管理中学到了什么”进一步提升“教”的能力!
、在文化背景的引导下,在反思中,坚持我们的收获,努力提高“品质”。
1、教研活动:教师研讨课严格按照我们“流程”进行,资料积累到位,一学期中每位教师要求自己上一节“好课。”
2、年级组工作:常规性的幼儿活动以年级组为单位展开,本学
5.2 探索轴对称的性质
复习回顾
观察下面几组图片和图形,哪些是轴对称图形,哪些是成轴对称
轴对称图形: 成轴对称:
①
②
③
④
⑤
⑥
A
B
C
A/
B/
C/
全等与成轴对称的关系:
成轴对称的两个图形一定全等,但全等的两个图形不一定成轴对称
对应点: 沿对称轴折叠后,能够重合的一对点叫对应点
对应线段:沿对称轴折叠后,能够重合的一组线段叫对应线段
对应角: 沿对称轴折叠后,能够重合的一对角叫对应角
扎字实验
如图5-5,将一张矩形纸对折,然后用笔尖扎出“14’’这个数字,将纸打开后铺平.
(1)图中折痕两旁的“14”有什么关系
(2)在扎字的过程中,点E与点E'重合,点F与点F'重合.设折痕所在直线为l,连接点E与点E'的线段EE'与直线l有什么关系 连接点F与点F'的线段呢
(3)线段AB与线段A'B'有什么关系 线段CD与线段C'D'呢
(4)∠1与∠2有什么关系 ∠3与∠4呢 说说你的理由.
∠1=∠2,∠3=∠4.
折痕两旁的“14”关于直线l对称.
都能被直线l垂直平分.
线段AB=线段A'B',线段CD=线段C'D'.
A
B
C
D
D1
C1
A1
B1
3
4
1
2
做一做:
右图是一个轴对称图形:
(1)找出它的对称轴及成轴对称的两个部分
(2)连接点A与点A1的线段与对称轴有什么关系?连接点B与点B1的线段呢?
对应点所连的线段被对称轴垂直平分.
A
B
C
D
D1
C1
A1
B1
3
4
1
2
(3)线段AD与线段A1D1有什么关系?线段BC与B1C1呢?为什么?
(4)∠1与∠2有什么关系 ∠ 3与∠4呢?说说你的理由?
对应角相等.
对应线段相等,
在轴对称图形或两个成轴对称的图形中:
1.对应点所连的线段被对称轴垂直平分
2.对应线段相等
3.对应角相等
根据轴对称的性质进行一次实战演习
轴对称性质的应用
(1)给你一个点A,你能找到并画出点A关于直线l的对应点A'吗 你是如何做的 与同伴交流.
如图所示,①过A点画AO⊥l于O点;
②延长AO到点A'使OA'=AO.
所以点A'就是点A关于直线l的对应点.
若两点所连线段被某直线垂直平分,则此直线为这两点的对称轴;
O
A'
(2)同学们能够画出一个点的对称点,那么如果老师给的是一条线段呢 如图,画出线段AB关于直线l成轴对称的线段A'B'.
A'
B'.
3. 画出△ABC关于直线l的对称图形.
解:如图所示.
方法总结:先确定一些关键的点(线段端点,三角形的顶点),然后作这些关键点的对称点,连接这些对称点即可.
1.如果两个图形关于某条直线对称,那么对应点所
连的线段被__________垂直平分.
2.下图是轴对称图形,相等的线段是____________
________,相等的角是__________.
A
B
C
D
E
对称轴
AB=CD,
BE=CE
∠B=∠C
当堂练习
3.两个图形关于某直线对称,对称点一定 ( ) A.这直线的两旁 B.这直线的同旁
C.这直线上 D.这直线两旁或这直线上
D
4.轴对称图形沿对称轴对折后,对称轴两旁的
部分( )
A.完全重合 B.不完全重合
C.两者都有
A
实战演练
5.如图,△ABC与△A1B1C1关于直线l对称,则∠B
为______.
解析:由轴对称的性质可得∠A1=∠A=50°, ∠C=∠C1=30°,所以∠B=∠B1=180°-50°-30°=100°.
100°
后面还有智力测验,你想试一试吗?
1. 一个汽车车牌在水中的倒影如图所示,你能确定该车的牌照号码吗?
你的眼力
下面哪一面镜子里是他像?
( D )
3、一次晚会上,主持人出了一道题目:“如何把 变成一个真正的等式?”过了很长时间,也没有人答出。
小兰仅仅拿了一面镜子,就很快解决了这道题目。
你知道她是怎样做的吗?
你知道为什么吗?
如图,宿州市要修建两个水上公园A,B,要在新汴河边修建一个水泵站向A,B两地送水,修在什么地方所用的水管最短?
A
B
实战演练
A
′
.
.
.
P
O
本节课学习了_________
学会了_________
感受了_________
作业
基础性作业:
画一个轴对称图形,并标明对称轴;
感谢语:
谢谢各位老师的光临!感谢大家的支持!
您的鼓励是我前进的动力!
再见!
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
