北师大版七年级数学下册 第五章5.3.3简单的轴对称图形 (共15张PPT)
文档属性
| 名称 | 北师大版七年级数学下册 第五章5.3.3简单的轴对称图形 (共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 427.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-03 14:51:27 | ||
图片预览






文档简介
七年级数学下册第五章5.3.3
简单的轴对称图形
一、学习目标
1.???通过实践操作与思考,经历探索简单图形轴对称性的过程,进一步体验轴对称的特征,发展空间观念.
2.掌握掌握角的平分线的性质和作已知角的平分线的方法。
二、温故知新
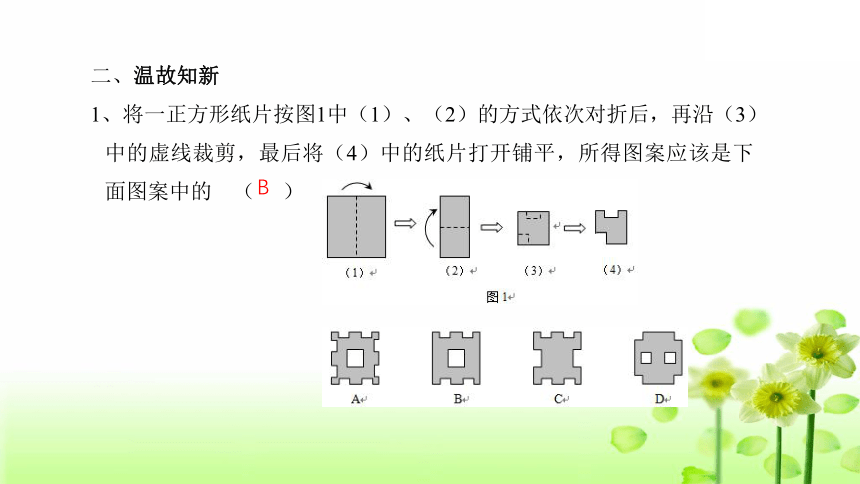
1、将一正方形纸片按图1中(1)、(2)的方式依次对折后,再沿(3)中的虚线裁剪,最后将(4)中的纸片打开铺平,所得图案应该是下面图案中的 ( )
B
三、自主探究:阅读课本p125-126
探究(一)角也是轴对称图形
1、动手操作:画出一个任意角∠AOB,将画出的∠AOB对折,使角的两边完全重合,然后用直尺画出折痕OM,回答问题:
(1)射线OM是∠AOB的 。
A、中线 B、高线 C、角平分线
(2)∠AOB是轴对称图形吗?它的对称轴是什么?
结论:角的轴对称性:
角是 图形,角的平分线所在的 就是它的对称轴。
C
∠AOB是轴对称图形
它的对称轴是角平分线所在直线
轴对称
直线
(3)如图,在∠AOB的平分线 OM上任取一点P,过点P分别向OA、OB作垂线,垂足为C和D,线段PC和线段PD有怎样的数量关系?请说明理由。
结论:
角平分线的性质: 的点到这个角的两边的距离 。
注意:使用角平分线的性质时必须具备两个条件:
①在角平分线上; ②过这点作角两边的垂线段。(两个条件缺一不可
解:PC=PD
理由: ∵ OM是∠AOB的平分线,
∴ ∠AOM=∠BOM
∵ CP ⊥ OA,DP ⊥ OB
∴ ∠PCO=∠PDO
∵ OP=OP
∴ △OPC ≌ △OPD
∴ PC=PD
角平分线上
相等
利用尺规,作∠AOB的平分线。(不写作法,保留作图痕迹)
问题:(1)为什么要“以大于12DE的长度为半径”?
(2)为什么OC是∠AOB平分线?你能证明吗?
?
若小于12DE的长度的一半为半径画弧,两弧不能相交
若等于12DE的长度的一半为半径画弧,两弧只有一个交点
所以只有大于12DE的长度的一半为半径画弧,两弧才能相交于两点
?
例1、如图,OP平分∠AOB,PC⊥OA于C,PD⊥OB于D,则PC与PD的大小关系是( )
A.PC>PD B.PC=PD C.PC<PD D.不能确定
例2、在Rt△ABC中,BD是∠ABC的平分线,DE⊥AB,垂足为E,DE与DC相等吗?为什么?
B
解:DE=DC
∵BD平分∠ABC的
∴∠EBD=∠CBD
∵DE⊥AB
∴∠BED=∠BCD=90°
∴△DBE ≌ △DBC(AAS)
∴DE=DC
四.随堂练习:
1.先任意画一个角,然后将它四等分.
解: ∵ BC=10,BD=6,
∴ CD=4
过D作DE⊥AB与E
∵ ∠C=90°,∠1=∠2,
∴ CD=DE=4
∴点D到边AB的距离是4
2.如图,已知∠C=90°,∠1=∠2,若BC=10,BD=6,求点D到边AB的距离。
五、小结:
1、角是轴对称图形,它的对称轴是 ,角的平分线上的点到这个角的两边的距离_______。
2、线段是轴对称图形,它的一条对称轴是 ,另一条对称轴是线段所在的直线。
3、线段垂直平分线上的点到这条线段 。
角平分线所在直线
相等
相等的垂直平分线
两端的距离相等
六.当堂检测:
1.下列图形中,不是轴对称图形的是( ).
A.角 B.等边三角形 C.线段 D.平行四边形
2、判断对错并说明理由
(1)∵ 如图(1),AD平分∠BAC(已知)
∴ BD = CD (在角的平分线上的点到这个角的两边的距离相等)
(2)∵ 如图(2), DC⊥AC,DB⊥AB (已知)
∴ BD = CD (在角的平分线上的点到这个角的两边的距离相等)
(1) (2)
D
错,因为没有指明DB,DC是点D到∠BAC两边的距离
错,因为没有指明AD是∠BAC的平分线
3、如图,直线a,b,c表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,可供选择的地址有几处?如何选?
可供选择的地址有4处:分别作△ABC的内角和外角的平分线,交点????1,????2,????3,????4,即为所选择的位置
?
分析:AC的长可分为AD和CD两部分,根据角平分线的性质可得DC=DE=1,根据线段垂直平分线的性质可得DA=DB=2.
解:∵ BD平分∠ABC,∠C=90°,DE⊥AB,
∴ DC=DE=1;
∵ DE⊥AB,E为AB的中点,
∴ DA=DB=2;
AC=DC+DA=1+2=3.
4.如图5-2所示,在△ABC中,∠C=90°,BD平分∠ABC,交AC于点D,过点D作DE⊥AB于点E,点E恰为AB的中点,若DE=1,BD=2,求AC的长.
5.如图,校园有两条路OA、OB,在交叉口附近有两块宣传牌C、D,学校准备在这里安装一盏路灯,要求灯柱的位置P离两块宣传牌一样远,并且到两条路的距离也一样远,请你帮助画出灯柱的位置点P,并说明理由.
解:作∠AOB的平分线OE,作线段CD的垂直平分线FH,OE与FH相交于点P,则点P就是灯柱的位置。
理由: ∵ OE平分∠AOB,点P在OE上
∴点P到∠AOB两边的距离相等
∵ FH是线段CD的垂直平分线,点P在FH上
∴点P到点C,D的距离相等
6.如图,在△ABC中,已知AB=AC,∠BAC和∠ACB的平分线相交于点D, ∠ADC=125°. 求∠ACB和∠BAC的度数.
解:∵AB=AC,AE平分∠BAC,
∴AE⊥BC(等腰三角形三线合一),
∵∠ADC=125°,
∴∠CDE=55°,
∴∠DCE=90°-∠CDE=35°,
又∵CD平分∠ACB,
∴∠ACB=2∠DCE=70°.
又∵AB=AC,
∴∠B=∠ACB=70°,
∴∠BAC=180-(∠B+∠ACB)=40°.
7.如图,在△ABC中,AB=AC,∠A=40°,点P为△ABC内的一点,
且∠PBC=∠PCA,则∠BPC的大小为 ( )
A.110° B.120° C.130° D.140°
A
∵在△ABC中,AB=AC,∠A=40°,
∴∠ACB=∠ABC=70°.
又∵∠PBC=∠PCA,
∴∠PBC+∠PCB=70°,
∴∠BPC=110°.
简单的轴对称图形
一、学习目标
1.???通过实践操作与思考,经历探索简单图形轴对称性的过程,进一步体验轴对称的特征,发展空间观念.
2.掌握掌握角的平分线的性质和作已知角的平分线的方法。
二、温故知新
1、将一正方形纸片按图1中(1)、(2)的方式依次对折后,再沿(3)中的虚线裁剪,最后将(4)中的纸片打开铺平,所得图案应该是下面图案中的 ( )
B
三、自主探究:阅读课本p125-126
探究(一)角也是轴对称图形
1、动手操作:画出一个任意角∠AOB,将画出的∠AOB对折,使角的两边完全重合,然后用直尺画出折痕OM,回答问题:
(1)射线OM是∠AOB的 。
A、中线 B、高线 C、角平分线
(2)∠AOB是轴对称图形吗?它的对称轴是什么?
结论:角的轴对称性:
角是 图形,角的平分线所在的 就是它的对称轴。
C
∠AOB是轴对称图形
它的对称轴是角平分线所在直线
轴对称
直线
(3)如图,在∠AOB的平分线 OM上任取一点P,过点P分别向OA、OB作垂线,垂足为C和D,线段PC和线段PD有怎样的数量关系?请说明理由。
结论:
角平分线的性质: 的点到这个角的两边的距离 。
注意:使用角平分线的性质时必须具备两个条件:
①在角平分线上; ②过这点作角两边的垂线段。(两个条件缺一不可
解:PC=PD
理由: ∵ OM是∠AOB的平分线,
∴ ∠AOM=∠BOM
∵ CP ⊥ OA,DP ⊥ OB
∴ ∠PCO=∠PDO
∵ OP=OP
∴ △OPC ≌ △OPD
∴ PC=PD
角平分线上
相等
利用尺规,作∠AOB的平分线。(不写作法,保留作图痕迹)
问题:(1)为什么要“以大于12DE的长度为半径”?
(2)为什么OC是∠AOB平分线?你能证明吗?
?
若小于12DE的长度的一半为半径画弧,两弧不能相交
若等于12DE的长度的一半为半径画弧,两弧只有一个交点
所以只有大于12DE的长度的一半为半径画弧,两弧才能相交于两点
?
例1、如图,OP平分∠AOB,PC⊥OA于C,PD⊥OB于D,则PC与PD的大小关系是( )
A.PC>PD B.PC=PD C.PC<PD D.不能确定
例2、在Rt△ABC中,BD是∠ABC的平分线,DE⊥AB,垂足为E,DE与DC相等吗?为什么?
B
解:DE=DC
∵BD平分∠ABC的
∴∠EBD=∠CBD
∵DE⊥AB
∴∠BED=∠BCD=90°
∴△DBE ≌ △DBC(AAS)
∴DE=DC
四.随堂练习:
1.先任意画一个角,然后将它四等分.
解: ∵ BC=10,BD=6,
∴ CD=4
过D作DE⊥AB与E
∵ ∠C=90°,∠1=∠2,
∴ CD=DE=4
∴点D到边AB的距离是4
2.如图,已知∠C=90°,∠1=∠2,若BC=10,BD=6,求点D到边AB的距离。
五、小结:
1、角是轴对称图形,它的对称轴是 ,角的平分线上的点到这个角的两边的距离_______。
2、线段是轴对称图形,它的一条对称轴是 ,另一条对称轴是线段所在的直线。
3、线段垂直平分线上的点到这条线段 。
角平分线所在直线
相等
相等的垂直平分线
两端的距离相等
六.当堂检测:
1.下列图形中,不是轴对称图形的是( ).
A.角 B.等边三角形 C.线段 D.平行四边形
2、判断对错并说明理由
(1)∵ 如图(1),AD平分∠BAC(已知)
∴ BD = CD (在角的平分线上的点到这个角的两边的距离相等)
(2)∵ 如图(2), DC⊥AC,DB⊥AB (已知)
∴ BD = CD (在角的平分线上的点到这个角的两边的距离相等)
(1) (2)
D
错,因为没有指明DB,DC是点D到∠BAC两边的距离
错,因为没有指明AD是∠BAC的平分线
3、如图,直线a,b,c表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,可供选择的地址有几处?如何选?
可供选择的地址有4处:分别作△ABC的内角和外角的平分线,交点????1,????2,????3,????4,即为所选择的位置
?
分析:AC的长可分为AD和CD两部分,根据角平分线的性质可得DC=DE=1,根据线段垂直平分线的性质可得DA=DB=2.
解:∵ BD平分∠ABC,∠C=90°,DE⊥AB,
∴ DC=DE=1;
∵ DE⊥AB,E为AB的中点,
∴ DA=DB=2;
AC=DC+DA=1+2=3.
4.如图5-2所示,在△ABC中,∠C=90°,BD平分∠ABC,交AC于点D,过点D作DE⊥AB于点E,点E恰为AB的中点,若DE=1,BD=2,求AC的长.
5.如图,校园有两条路OA、OB,在交叉口附近有两块宣传牌C、D,学校准备在这里安装一盏路灯,要求灯柱的位置P离两块宣传牌一样远,并且到两条路的距离也一样远,请你帮助画出灯柱的位置点P,并说明理由.
解:作∠AOB的平分线OE,作线段CD的垂直平分线FH,OE与FH相交于点P,则点P就是灯柱的位置。
理由: ∵ OE平分∠AOB,点P在OE上
∴点P到∠AOB两边的距离相等
∵ FH是线段CD的垂直平分线,点P在FH上
∴点P到点C,D的距离相等
6.如图,在△ABC中,已知AB=AC,∠BAC和∠ACB的平分线相交于点D, ∠ADC=125°. 求∠ACB和∠BAC的度数.
解:∵AB=AC,AE平分∠BAC,
∴AE⊥BC(等腰三角形三线合一),
∵∠ADC=125°,
∴∠CDE=55°,
∴∠DCE=90°-∠CDE=35°,
又∵CD平分∠ACB,
∴∠ACB=2∠DCE=70°.
又∵AB=AC,
∴∠B=∠ACB=70°,
∴∠BAC=180-(∠B+∠ACB)=40°.
7.如图,在△ABC中,AB=AC,∠A=40°,点P为△ABC内的一点,
且∠PBC=∠PCA,则∠BPC的大小为 ( )
A.110° B.120° C.130° D.140°
A
∵在△ABC中,AB=AC,∠A=40°,
∴∠ACB=∠ABC=70°.
又∵∠PBC=∠PCA,
∴∠PBC+∠PCB=70°,
∴∠BPC=110°.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
