北师大版七年级数学下册第4章 4.5利用三角形全等测距离 (共22张PPT)
文档属性
| 名称 | 北师大版七年级数学下册第4章 4.5利用三角形全等测距离 (共22张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-03 14:51:49 | ||
图片预览



文档简介
北师大版七年级数学下册
山东省滕州市洪绪中学
(1)会利用三角形全等解决实际问题,体会数学与实际生活的联系。(重点)
(2)能从实例中构建全等三角形,体会转化思想。
(重点、难点)
(3)在利用三角形全等解决问题的过程中能进行有条理的思考和表达。(难点)
学习目标
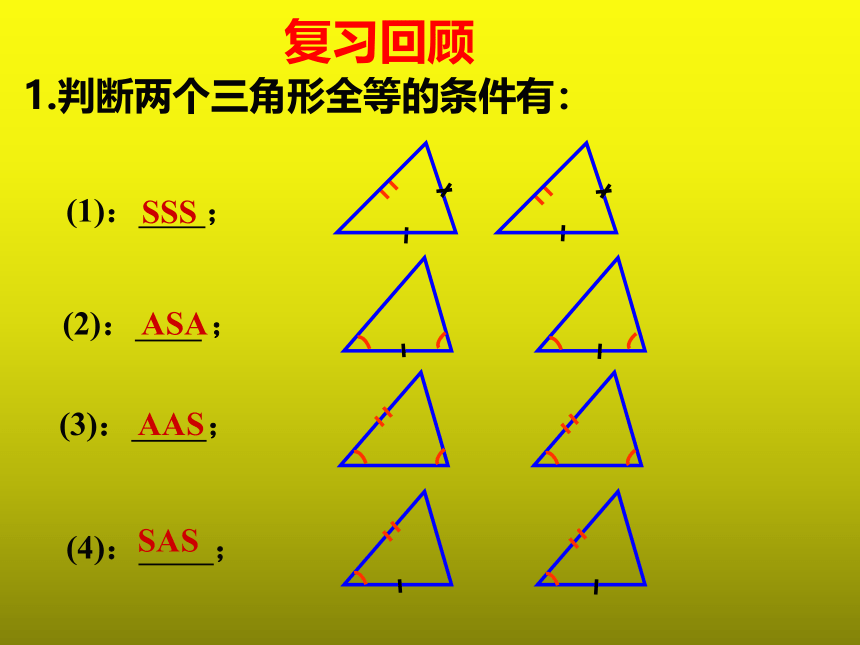
1.判断两个三角形全等的条件有:
(1): ;
(2): ;
(3): ;
SSS
ASA
AAS
复习回顾
(4): ;
SAS
2.全等三角形有什么性质是?
?全等三角形的对应角相等
?全等三角形的对应边相等
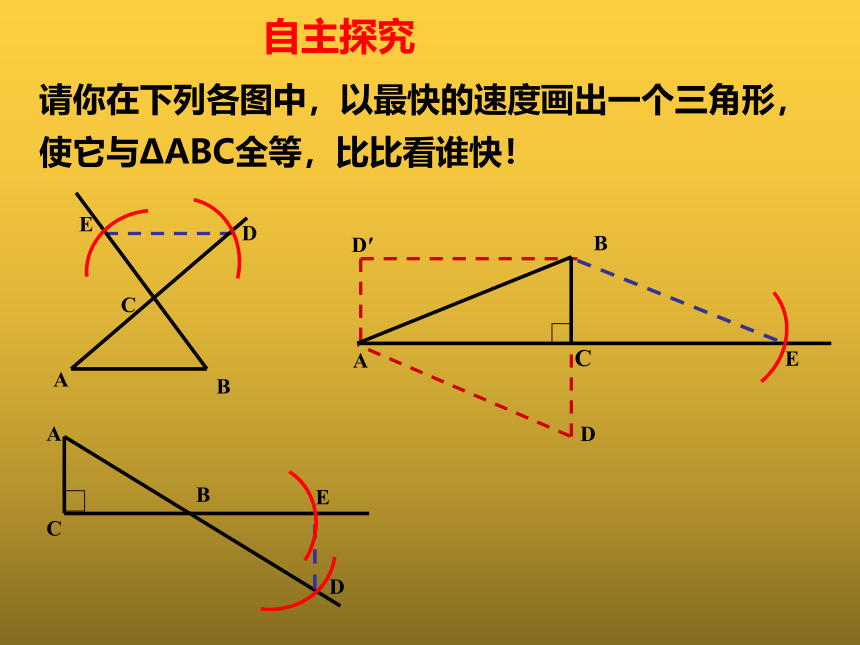
请你在下列各图中,以最快的速度画出一个三角形,使它与ΔABC全等,比比看谁快!
A
B
C
A
C
B
A
C
B
D′
D
E
D
E
E
D
自主探究
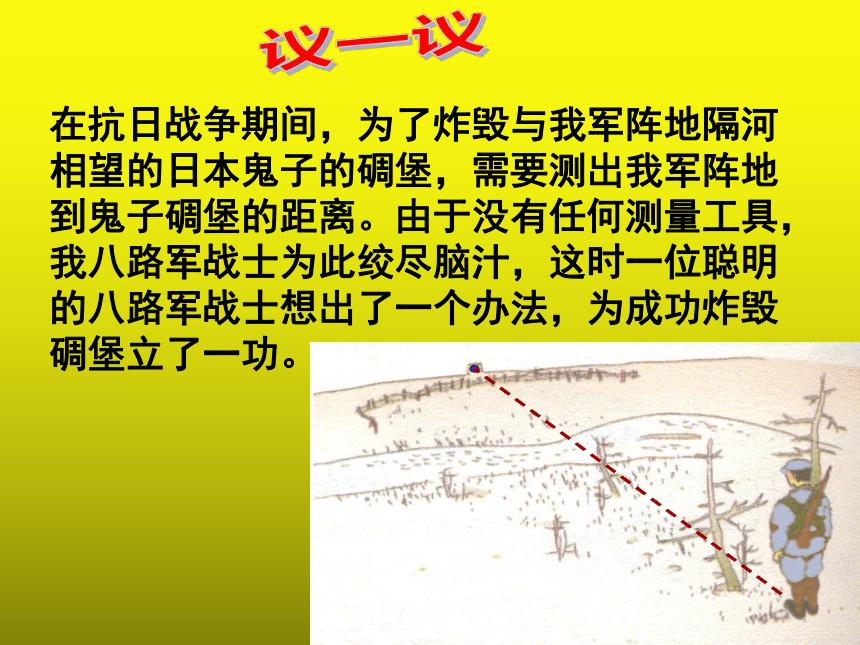
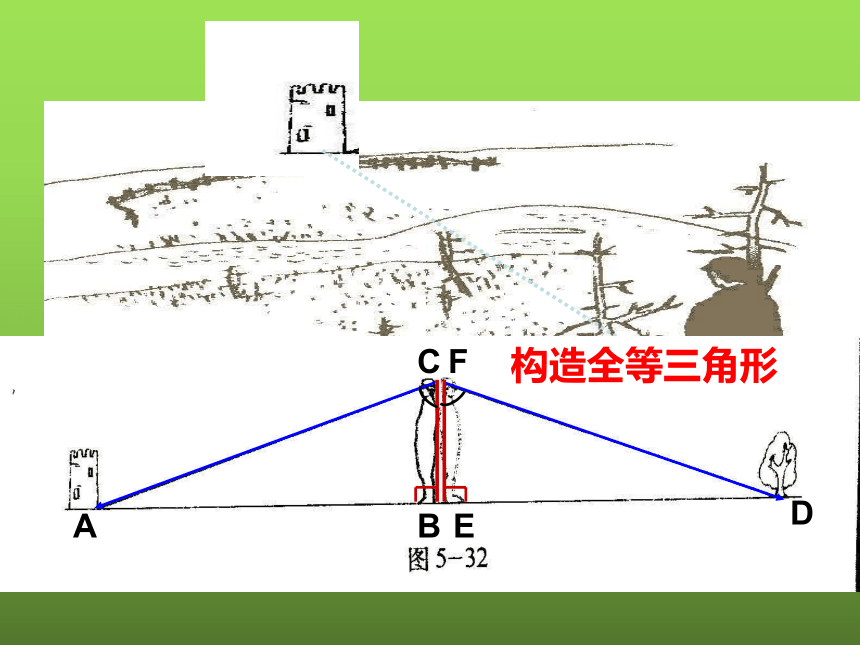
在抗日战争期间,为了炸毁与我军阵地隔河相望的日本鬼子的碉堡,需要测出我军阵地到鬼子碉堡的距离。由于没有任何测量工具,我八路军战士为此绞尽脑汁,这时一位聪明的八路军战士想出了一个办法,为成功炸毁碉堡立了一功。
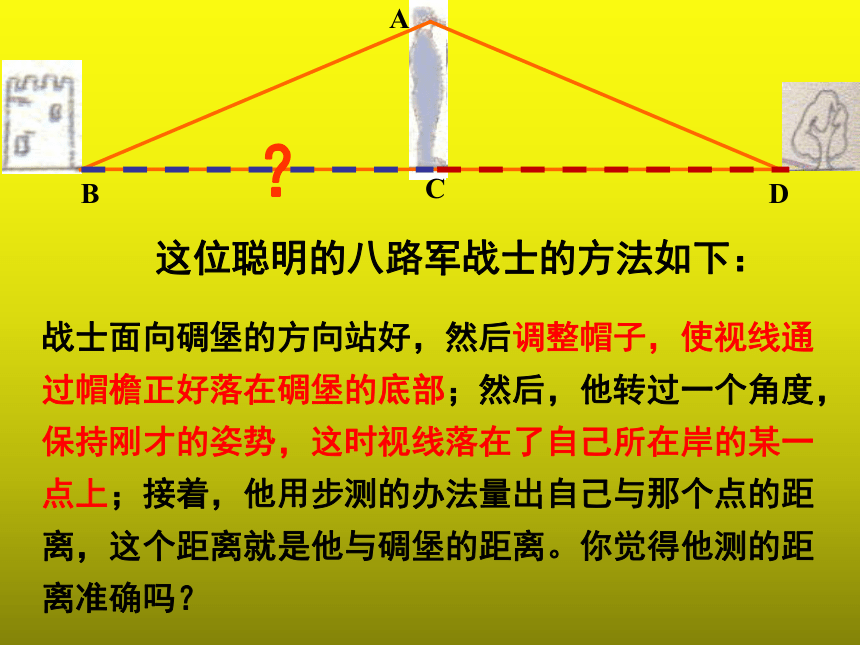
这位聪明的八路军战士的方法如下:
战士面向碉堡的方向站好,然后调整帽子,使视线通过帽檐正好落在碉堡的底部;然后,他转过一个角度,保持刚才的姿势,这时视线落在了自己所在岸的某一点上;接着,他用步测的办法量出自己与那个点的距离,这个距离就是他与碉堡的距离。你觉得他测的距离准确吗?
A
C
B
D
?
F
E
D
C
B
A
构造全等三角形
∴BC= DC( )
A
C
B
D
?
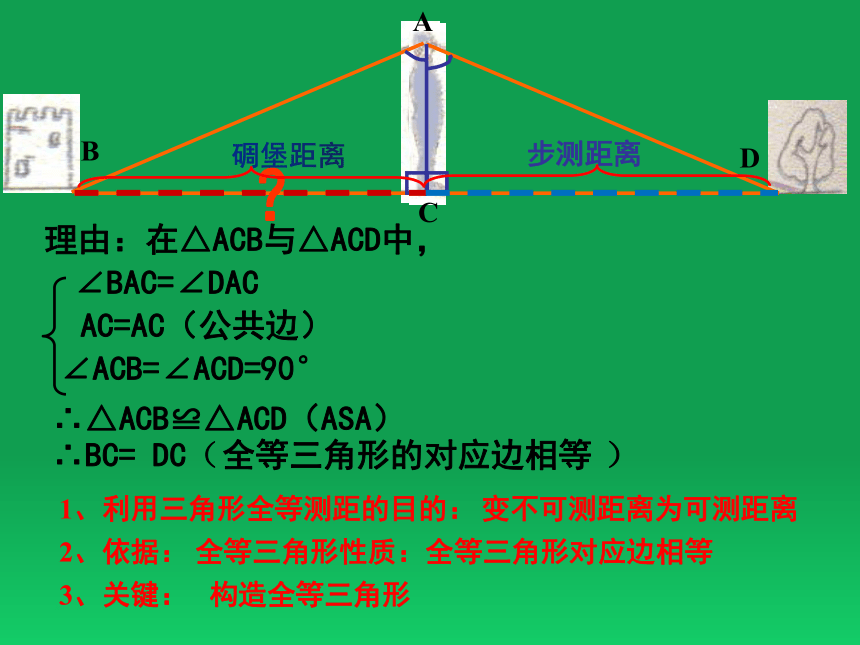
理由:在△ACB与△ACD中,
∠BAC=∠DAC
AC=AC(公共边)
∠ACB=∠ACD=90°
∴△ACB≌△ACD(ASA)
全等三角形的对应边相等
步测距离
1、利用三角形全等测距的目的:
2、依据:
3、关键:
变不可测距离为可测距离
全等三角形性质:全等三角形对应边相等
构造全等三角形
小明在上周末游览风景
区时,看到了一个美丽的
池塘 ,他想知道最远两点
A、B之间的距离,但是他没有船,不能直接去测量。
手里只有一根绳子和一把尺子,他怎样才能测出A、
B之间的距离呢?
把你的设计方案在图上画出来,并与你的同伴
交流你的方案,看看谁的方案更便捷。
A
B
●
●
A、B间有多远呢?
A
B
●
●
C
E
D
在能够到达A、B的空地上取一适当点C,连接AC,并延长AC到D,使CD=AC,连接BC,并延长BC到E,使CE=BC,连接ED。则只要测出ED的长就可以知道AB的长了。
理由如下: 在ΔACB与ΔDCE中,
∠BCA=∠ECD(对顶角相等)
AC= DC(已知)
BC=CE(已知)
∴ΔACB≌ΔDCE(SAS)
∴AB=DE( 全等三角形的对应边相等)
方案一
方法总结:
延长线法
●
在AB的垂线BF上取两点C、D,使CD=BC.再过D点作出BF的垂线DG,并在DG上找一点E,使A、C、E在一条直线上。这时测得的DE的长就是A 、 B间距离.
F
D
E
C
A
B
在△ACB与△ECD中,
证明:
∠ABC=∠EDC=90°(已知)
BC=DC(已知)
∠ACB=∠ECD(对顶角相等)
G
方案二
方法总结:垂直法
∴△ACB≌△ECD ( ASA)
∴AB=DE( 全等三角形的对应边相等)
小结
1、知识:
利用三角形全等测距离的目的:
变不可测距离为可测距离。
依据:
全等三角形性质。
关键:
构造全等三角形。
2、方法:
(1)延长法构造全等三角形;
(2)垂直法构造全等三角形;
3、数学思想:
树立用三角形全等构建数学模型解决实际问题的思想。
1.如图所示小明设计了一种测工件内径AB的卡钳,问:在卡钳的设计中,AO、BO、CO、DO 应满足下列的哪个条件?( )
A、AO=CO
B、BO=DO
C、AC=BD
D、AO=CO且BO=DO
D
O
D
C
B
A
检测练习
2、如图要测量河两岸相对的两点A、B的距离,先在AB 的垂线BF上取两点C、D,使CD=BC,再定出BF的垂线DE,可以证明△EDC≌△ABC,得ED=AB,因此,测得ED的长就是AB的长。判定△EDC≌△ABC的理由是( )
A、SSS B、ASA C、AAS D、SAS
B
A
●
●
D
C
E
F
B
3、如图,工人师傅要计算一个圆柱形容器的容积,需要测量其内径。现在有两根同样长的木棒、一条橡皮绳和一把带有刻度的直尺,你能想法帮助他完成吗?
·
中点O
A
B
C
D
用直尺量出两根木棒AC、BD的中点O,用橡皮筋把两个中点固定在一起,再把两根木棒的一头C、D放进容器内,调整角度使C、D紧贴容器内壁,在容器外部测量AB的长度就是容器内径CD的长。利用SAS判断△AOB≌△ COD
在△AOB与△COD中,
证明:
AO=CO
∠AOB= ∠COD
BO=DO
∴△AOB≌△COD ( SAS)
∴AB=CD (全等三角形的对应边相等)
4、如图,山脚下有A、B两点,要测出A、B两点的距离。
(1)在地上取一个可以直接到达A、B点的点O,连接AO
并延长AO到C,使AO=CO,你能完成剩下的图形吗?
A
B
(2)说明你是如何求AB的距离。
?
?
D
C
解:在△AOB与△COD中,
AO = CO(已知)
∠ AOB = ∠COD(对顶角相等)
BO = DO(已知)
∴△AOB≌△ COD(SAS)
∴ AB=CD(全等三角形的对应边相等)
所以通过测量C、D之间的距离可以求A、B的距离
O
连接BO并延长BO到D,使BO=DO,测得CD的长就是A、B间的距离。
4、如图,山脚下有A、B两点,要测出A、B两点的距离。
你能垂直法设计求AB间距离吗?
并说明你的理由!
A
B
?
?
D
C
O
解:在△AOB与△COD中,
∠BAO =∠DCO(已知)
∠ AOB = ∠COD(对顶角相等)
AO = CO(已知)
∴△AOB≌△ COD(ASA)
∴ AB=CD (全等三角形的对应边相等)
所以通过测量C、D之间的距离可以求A、B的距离
在AB的垂线AC上取两点O、C,使AO=CO,过点C作AC的垂线交BO的延长线于点D,测得CD的长即为A、B间的距离。
6.如图,小颖为了测量B点到河对岸的目标A的距离,她在B 的同侧选择了一点C,测得∠ABC=70°,∠ACB=40°,然后在M处立了标杆,使∠CBM=70°,
1.她应该怎样做才能测得A、B之间的距离?
2.画出完整图形,并说根据图形明理由。
40°
D
1.以点C为顶点BC为一边在另一侧作∠BCD=40°,测得BD的长就等于AB间的距离。
2.解:在△ABC与△DBC中
∠ABC=∠DBC=70°(已知)
BC=BC (公共边)
∠ACB=∠DCB=40°(已知)
∴△ABC≌△DBC (ASA)
∴AB=DB (全等三角形的对应边相等)
所以通过测量B、D之间的距离可以求A、B的距离
7.为了测量一幢高楼的高度AB,在旗杆CD与楼之间选定一点P.测得旗杆顶C视线PC与地面夹角∠DPC=38°,测得楼顶A视线PA与地面夹角∠APB=52°,量得点P到楼底距离PB与旗杆高度相等,等于8米,量得旗杆与楼之间距离为DB=33米,计算楼高AB是多少米?
解:∵∠CPD=38°,∠APB=52°
∠CDP=∠ABP=90°,
∴∠DCP=∠APB=52°
在△CPD和△PAB中
∠CDP=∠ABP=90°
DC=PB
∠DCP=∠APB
∴△CPD≌△PAB(ASA)
∴ DP=AB
因为DB=33米,PB=8米,所以AB=33-8=25(米)
答:楼高AB是25米 .
38°
52°
∟
∟
布置作业
完成助学113--116页4.5“利用三角形全等测距离”
谢谢!下课!
2019
不负过去
2020
不惧未来
山东省滕州市洪绪中学
(1)会利用三角形全等解决实际问题,体会数学与实际生活的联系。(重点)
(2)能从实例中构建全等三角形,体会转化思想。
(重点、难点)
(3)在利用三角形全等解决问题的过程中能进行有条理的思考和表达。(难点)
学习目标
1.判断两个三角形全等的条件有:
(1): ;
(2): ;
(3): ;
SSS
ASA
AAS
复习回顾
(4): ;
SAS
2.全等三角形有什么性质是?
?全等三角形的对应角相等
?全等三角形的对应边相等
请你在下列各图中,以最快的速度画出一个三角形,使它与ΔABC全等,比比看谁快!
A
B
C
A
C
B
A
C
B
D′
D
E
D
E
E
D
自主探究
在抗日战争期间,为了炸毁与我军阵地隔河相望的日本鬼子的碉堡,需要测出我军阵地到鬼子碉堡的距离。由于没有任何测量工具,我八路军战士为此绞尽脑汁,这时一位聪明的八路军战士想出了一个办法,为成功炸毁碉堡立了一功。
这位聪明的八路军战士的方法如下:
战士面向碉堡的方向站好,然后调整帽子,使视线通过帽檐正好落在碉堡的底部;然后,他转过一个角度,保持刚才的姿势,这时视线落在了自己所在岸的某一点上;接着,他用步测的办法量出自己与那个点的距离,这个距离就是他与碉堡的距离。你觉得他测的距离准确吗?
A
C
B
D
?
F
E
D
C
B
A
构造全等三角形
∴BC= DC( )
A
C
B
D
?
理由:在△ACB与△ACD中,
∠BAC=∠DAC
AC=AC(公共边)
∠ACB=∠ACD=90°
∴△ACB≌△ACD(ASA)
全等三角形的对应边相等
步测距离
1、利用三角形全等测距的目的:
2、依据:
3、关键:
变不可测距离为可测距离
全等三角形性质:全等三角形对应边相等
构造全等三角形
小明在上周末游览风景
区时,看到了一个美丽的
池塘 ,他想知道最远两点
A、B之间的距离,但是他没有船,不能直接去测量。
手里只有一根绳子和一把尺子,他怎样才能测出A、
B之间的距离呢?
把你的设计方案在图上画出来,并与你的同伴
交流你的方案,看看谁的方案更便捷。
A
B
●
●
A、B间有多远呢?
A
B
●
●
C
E
D
在能够到达A、B的空地上取一适当点C,连接AC,并延长AC到D,使CD=AC,连接BC,并延长BC到E,使CE=BC,连接ED。则只要测出ED的长就可以知道AB的长了。
理由如下: 在ΔACB与ΔDCE中,
∠BCA=∠ECD(对顶角相等)
AC= DC(已知)
BC=CE(已知)
∴ΔACB≌ΔDCE(SAS)
∴AB=DE( 全等三角形的对应边相等)
方案一
方法总结:
延长线法
●
在AB的垂线BF上取两点C、D,使CD=BC.再过D点作出BF的垂线DG,并在DG上找一点E,使A、C、E在一条直线上。这时测得的DE的长就是A 、 B间距离.
F
D
E
C
A
B
在△ACB与△ECD中,
证明:
∠ABC=∠EDC=90°(已知)
BC=DC(已知)
∠ACB=∠ECD(对顶角相等)
G
方案二
方法总结:垂直法
∴△ACB≌△ECD ( ASA)
∴AB=DE( 全等三角形的对应边相等)
小结
1、知识:
利用三角形全等测距离的目的:
变不可测距离为可测距离。
依据:
全等三角形性质。
关键:
构造全等三角形。
2、方法:
(1)延长法构造全等三角形;
(2)垂直法构造全等三角形;
3、数学思想:
树立用三角形全等构建数学模型解决实际问题的思想。
1.如图所示小明设计了一种测工件内径AB的卡钳,问:在卡钳的设计中,AO、BO、CO、DO 应满足下列的哪个条件?( )
A、AO=CO
B、BO=DO
C、AC=BD
D、AO=CO且BO=DO
D
O
D
C
B
A
检测练习
2、如图要测量河两岸相对的两点A、B的距离,先在AB 的垂线BF上取两点C、D,使CD=BC,再定出BF的垂线DE,可以证明△EDC≌△ABC,得ED=AB,因此,测得ED的长就是AB的长。判定△EDC≌△ABC的理由是( )
A、SSS B、ASA C、AAS D、SAS
B
A
●
●
D
C
E
F
B
3、如图,工人师傅要计算一个圆柱形容器的容积,需要测量其内径。现在有两根同样长的木棒、一条橡皮绳和一把带有刻度的直尺,你能想法帮助他完成吗?
·
中点O
A
B
C
D
用直尺量出两根木棒AC、BD的中点O,用橡皮筋把两个中点固定在一起,再把两根木棒的一头C、D放进容器内,调整角度使C、D紧贴容器内壁,在容器外部测量AB的长度就是容器内径CD的长。利用SAS判断△AOB≌△ COD
在△AOB与△COD中,
证明:
AO=CO
∠AOB= ∠COD
BO=DO
∴△AOB≌△COD ( SAS)
∴AB=CD (全等三角形的对应边相等)
4、如图,山脚下有A、B两点,要测出A、B两点的距离。
(1)在地上取一个可以直接到达A、B点的点O,连接AO
并延长AO到C,使AO=CO,你能完成剩下的图形吗?
A
B
(2)说明你是如何求AB的距离。
?
?
D
C
解:在△AOB与△COD中,
AO = CO(已知)
∠ AOB = ∠COD(对顶角相等)
BO = DO(已知)
∴△AOB≌△ COD(SAS)
∴ AB=CD(全等三角形的对应边相等)
所以通过测量C、D之间的距离可以求A、B的距离
O
连接BO并延长BO到D,使BO=DO,测得CD的长就是A、B间的距离。
4、如图,山脚下有A、B两点,要测出A、B两点的距离。
你能垂直法设计求AB间距离吗?
并说明你的理由!
A
B
?
?
D
C
O
解:在△AOB与△COD中,
∠BAO =∠DCO(已知)
∠ AOB = ∠COD(对顶角相等)
AO = CO(已知)
∴△AOB≌△ COD(ASA)
∴ AB=CD (全等三角形的对应边相等)
所以通过测量C、D之间的距离可以求A、B的距离
在AB的垂线AC上取两点O、C,使AO=CO,过点C作AC的垂线交BO的延长线于点D,测得CD的长即为A、B间的距离。
6.如图,小颖为了测量B点到河对岸的目标A的距离,她在B 的同侧选择了一点C,测得∠ABC=70°,∠ACB=40°,然后在M处立了标杆,使∠CBM=70°,
1.她应该怎样做才能测得A、B之间的距离?
2.画出完整图形,并说根据图形明理由。
40°
D
1.以点C为顶点BC为一边在另一侧作∠BCD=40°,测得BD的长就等于AB间的距离。
2.解:在△ABC与△DBC中
∠ABC=∠DBC=70°(已知)
BC=BC (公共边)
∠ACB=∠DCB=40°(已知)
∴△ABC≌△DBC (ASA)
∴AB=DB (全等三角形的对应边相等)
所以通过测量B、D之间的距离可以求A、B的距离
7.为了测量一幢高楼的高度AB,在旗杆CD与楼之间选定一点P.测得旗杆顶C视线PC与地面夹角∠DPC=38°,测得楼顶A视线PA与地面夹角∠APB=52°,量得点P到楼底距离PB与旗杆高度相等,等于8米,量得旗杆与楼之间距离为DB=33米,计算楼高AB是多少米?
解:∵∠CPD=38°,∠APB=52°
∠CDP=∠ABP=90°,
∴∠DCP=∠APB=52°
在△CPD和△PAB中
∠CDP=∠ABP=90°
DC=PB
∠DCP=∠APB
∴△CPD≌△PAB(ASA)
∴ DP=AB
因为DB=33米,PB=8米,所以AB=33-8=25(米)
答:楼高AB是25米 .
38°
52°
∟
∟
布置作业
完成助学113--116页4.5“利用三角形全等测距离”
谢谢!下课!
2019
不负过去
2020
不惧未来
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
