北师大版七年级下册 3.1用表格表示的变量间关系专题提升(共20张PPT)
文档属性
| 名称 | 北师大版七年级下册 3.1用表格表示的变量间关系专题提升(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-03 14:53:03 | ||
图片预览








文档简介
3.1用表格表示的变量间关系
课堂目标
(1)在具体情境中理解什么是变量、自变量、因变量,并能举出反映变量之间关系的例子
(2)能从表格中获得变量之间关系的信息,能用表格表示两个变量之间的关系,并根据表格中的数据尝试对变化趋势进行初步的预测
物体质量x和弹簧长度y都在变化,它们都是变量.
其中弹簧长度y随物体质量x的变化而变化,x是自变量,y是因变量
在这一变化过程中,弹簧的自然长度(80cm)始终没有变化.像这种在变化过程中数值始终不变的量叫做常量.
表格可以表示因变量随自变量变化而变化的情况。
概念回顾:
概念巩固
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}年数(年)
0
1
2
3
4
5
...
树高(米)
1.5
1.7
1.9
2.1
2.3
2.5
...
1.指出下列实例中的自变量与因变量。
(1)小树苗的生长情况如下表。 (2)圆的半径为r,周长C=2πr.
(3)小明背英语单词,每天背5个,随着时间的推移,他的词汇量越来越大
2.请你举出生活中反映变量之间关系的例子,并说出其中的自变量和因变量.
(1)水电费 (2)购物 (3)水龙头出水
巩固深化
1.我国从1949年到2009年的人口统计数据如下(精确到0.01亿):
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}时间/年
1959
1969
1979
1989
1999
2009
人口数量/亿
6.72
8.07
9.75
11.07
12.59
13.35
(1)如果用x表示时间,y表示我国人口总数,那么随着x的变化,y的变化趋势是什么?
(2)x和y哪个是自变量?哪个是因变量?
(3)从1949年起,时间每向后推移10年,我国人口是怎样的变化?
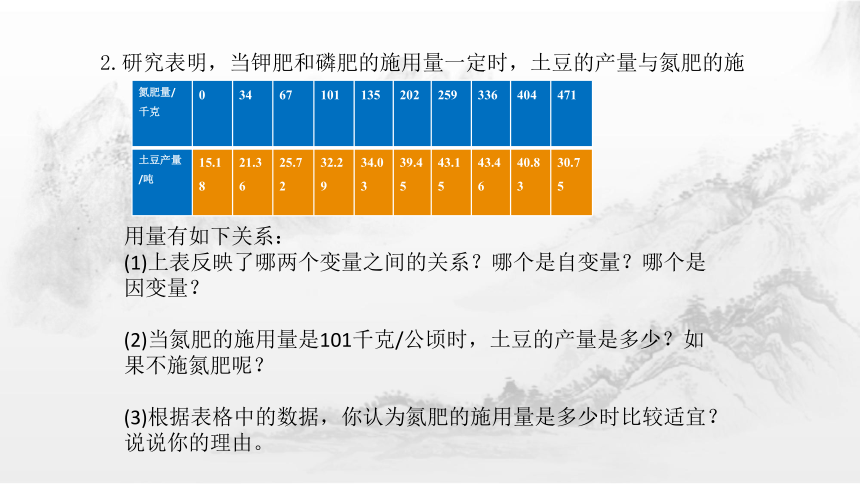
2.研究表明,当钾肥和磷肥的施用量一定时,土豆的产量与氮肥的施
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}氮肥量/千克
0
34
67
101
135
202
259
336
404
471
土豆产量/吨
15.18
21.36
25.72
32.29
34.03
39.45
43.15
43.46
40.83
30.75
用量有如下关系:
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当氮肥的施用量是101千克/公顷时,土豆的产量是多少?如果不施氮肥呢?
(3)根据表格中的数据,你认为氮肥的施用量是多少时比较适宜?说说你的理由。
当堂检测
1.指出下列实例中自变量与因变量
(1)随着时间推移,汽车在行驶中的剩余油量减少.
(2)烧一壶水,发现在一定时间内温度随时间的变化而变化,即随时间的增加,温度逐渐增高.
(3)农作物高度随种植时间的变化而变化
(4)乘坐出租车时,费用随行驶路程而变化
(5)圆柱的高是6cm,当圆柱的底面半径r由小到大变化时,圆柱的体积V也随之发生变化.
2.儿童从出生到10岁的体重变化。
婴儿在6个月、1周岁、2周岁时体重分别大约是出生时的2倍、3倍、4倍,6周岁、10周岁时体重分别约是1周岁时的2倍、3倍。
(1)上述的哪些量在发生变化?
(2)某婴儿在出生时的体重是3.5千克,请把他在发育过程中的体重情况填入下表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}年龄
刚出生
6个月
1周岁
2周岁
6周岁
10周岁
体重/千克
?
?
?
?
?
?
(3)根据表中的数据,说一说儿童从出生到10周岁之间体重是怎样随着年龄的增长而变化的。
3.已知某易拉罐厂设计一种易拉罐,在设计过程中发现符合要求的易拉罐的底面半径与用铝量有如下关系:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}底面半径x( cm)
1.6
2.0
2.4
2.8
3.2
3.6
4.0
用铝量y( cm3)
6.9
6.0
5.6
5.5
5.7
6.0
6.5
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当易拉罐底面半径为2.4 cm时,易拉罐需要的用铝量是多少?
(3)根据表格中的数据,你认为易拉罐的底面半径为多少时比较适宜?说说你的理由;
随堂练习
A.S,a是变量, h是常量 B.S,h是变量, 是常量
C.S,h是变量, a是常量 D.S,h,a是变量, 是常量
2.小丽烧一壶水,发现在一定时间内温度随时间的变化而变化,即随时间的增加,温度逐渐增高,如果用t表示时间,T表示温度,则_____是自变量,_____是因变量.
3.某河受暴雨袭击,某天此河水的水位记录为下表
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}时间/小时
0
4
8
12
16
20
24
水位/米
2
2.5
3
4
5
6
8
(1)上表中反映了哪两个变量之间的关系?自变量和因变量各是什么?
(2)12时,水位是多少?
(3)哪一时段水位上升最快?
4.下表是小华做观察水的沸腾实验时所记录的数据:
(1)时间是8分钟时,水的温度为_____;
(2)此表反映了变量_____和_____之间的关系,其中_____是自变量,_____是因变量;
(3)在_____时间内,温度随时间增加而增加;_____时间内,水的温度不再变化.
单击此处添加标题
文字内容
0
10
20
30
40
50
60
70
80
文字内容
文字内容
文字内容
文字内容
文字内容
文字内容
文字内容
文字内容
36
41
45
57
54
39
48
60
5.某电影院地面的一部分是扇形,座位按下列方式设置:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}排数
1
2
3
4
座位数
60
64
68
72
(1)上述哪些量在变化?自变量和因变量分别是什么?
(2)第5排、第6排各有多少个座位?
(3)第n排有多少个座位?请说明你的理由。
6.某电信公司提供了一种移动通讯服务的收费标准,如下表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}项目
月基本服务费
月免费通话时间
超出后每分收费
标准
40元
150分
0.6元
(1)上述哪些量在变化?自变量和因变量分别是什么?
(2)第5排、第6排各有多少个座位?
(3)第n排有多少个座位?请说明你的理由。
6.研究发现,地表以下岩层的温度与它所处的深度有表中的关系:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}岩层的深度h/km
1
2
3
4
5
6
…
岩层的温度t/℃
55
90
125
160
195
230
…
根据以上信息,回答下列问题:
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)岩层的深度h每增加1km,温度t是怎样变化的?
(3)估计岩层10km深处的温度是多少?
8.阅读下面这段有关“龟兔赛跑”的寓言故事,并指出所涉及的量中,哪些是常量,哪些是变量.
一次乌龟与兔子举行500米赛跑,比赛开始不久,兔子就遥遥领先.当兔子以20米/分的速度跑了10分时,往回一看,乌龟远远地落在后面呢!兔子心想:“我就是睡一觉,你乌龟也追不上我,我为何不在此美美地睡上一觉呢?”可是,当骄傲的兔子正做着胜利者的美梦时,勤勉的乌龟却从它身边悄悄爬过,并以10米/分的速度匀速爬向终点.40分后,兔子梦醒了,而此时乌龟刚好到达终点.兔子悔之晚矣,等它再以30米/分的速度跑向终点时,它比乌龟足足晚了10分.
谢谢观看
课堂目标
(1)在具体情境中理解什么是变量、自变量、因变量,并能举出反映变量之间关系的例子
(2)能从表格中获得变量之间关系的信息,能用表格表示两个变量之间的关系,并根据表格中的数据尝试对变化趋势进行初步的预测
物体质量x和弹簧长度y都在变化,它们都是变量.
其中弹簧长度y随物体质量x的变化而变化,x是自变量,y是因变量
在这一变化过程中,弹簧的自然长度(80cm)始终没有变化.像这种在变化过程中数值始终不变的量叫做常量.
表格可以表示因变量随自变量变化而变化的情况。
概念回顾:
概念巩固
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}年数(年)
0
1
2
3
4
5
...
树高(米)
1.5
1.7
1.9
2.1
2.3
2.5
...
1.指出下列实例中的自变量与因变量。
(1)小树苗的生长情况如下表。 (2)圆的半径为r,周长C=2πr.
(3)小明背英语单词,每天背5个,随着时间的推移,他的词汇量越来越大
2.请你举出生活中反映变量之间关系的例子,并说出其中的自变量和因变量.
(1)水电费 (2)购物 (3)水龙头出水
巩固深化
1.我国从1949年到2009年的人口统计数据如下(精确到0.01亿):
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}时间/年
1959
1969
1979
1989
1999
2009
人口数量/亿
6.72
8.07
9.75
11.07
12.59
13.35
(1)如果用x表示时间,y表示我国人口总数,那么随着x的变化,y的变化趋势是什么?
(2)x和y哪个是自变量?哪个是因变量?
(3)从1949年起,时间每向后推移10年,我国人口是怎样的变化?
2.研究表明,当钾肥和磷肥的施用量一定时,土豆的产量与氮肥的施
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}氮肥量/千克
0
34
67
101
135
202
259
336
404
471
土豆产量/吨
15.18
21.36
25.72
32.29
34.03
39.45
43.15
43.46
40.83
30.75
用量有如下关系:
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当氮肥的施用量是101千克/公顷时,土豆的产量是多少?如果不施氮肥呢?
(3)根据表格中的数据,你认为氮肥的施用量是多少时比较适宜?说说你的理由。
当堂检测
1.指出下列实例中自变量与因变量
(1)随着时间推移,汽车在行驶中的剩余油量减少.
(2)烧一壶水,发现在一定时间内温度随时间的变化而变化,即随时间的增加,温度逐渐增高.
(3)农作物高度随种植时间的变化而变化
(4)乘坐出租车时,费用随行驶路程而变化
(5)圆柱的高是6cm,当圆柱的底面半径r由小到大变化时,圆柱的体积V也随之发生变化.
2.儿童从出生到10岁的体重变化。
婴儿在6个月、1周岁、2周岁时体重分别大约是出生时的2倍、3倍、4倍,6周岁、10周岁时体重分别约是1周岁时的2倍、3倍。
(1)上述的哪些量在发生变化?
(2)某婴儿在出生时的体重是3.5千克,请把他在发育过程中的体重情况填入下表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}年龄
刚出生
6个月
1周岁
2周岁
6周岁
10周岁
体重/千克
?
?
?
?
?
?
(3)根据表中的数据,说一说儿童从出生到10周岁之间体重是怎样随着年龄的增长而变化的。
3.已知某易拉罐厂设计一种易拉罐,在设计过程中发现符合要求的易拉罐的底面半径与用铝量有如下关系:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}底面半径x( cm)
1.6
2.0
2.4
2.8
3.2
3.6
4.0
用铝量y( cm3)
6.9
6.0
5.6
5.5
5.7
6.0
6.5
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当易拉罐底面半径为2.4 cm时,易拉罐需要的用铝量是多少?
(3)根据表格中的数据,你认为易拉罐的底面半径为多少时比较适宜?说说你的理由;
随堂练习
A.S,a是变量, h是常量 B.S,h是变量, 是常量
C.S,h是变量, a是常量 D.S,h,a是变量, 是常量
2.小丽烧一壶水,发现在一定时间内温度随时间的变化而变化,即随时间的增加,温度逐渐增高,如果用t表示时间,T表示温度,则_____是自变量,_____是因变量.
3.某河受暴雨袭击,某天此河水的水位记录为下表
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}时间/小时
0
4
8
12
16
20
24
水位/米
2
2.5
3
4
5
6
8
(1)上表中反映了哪两个变量之间的关系?自变量和因变量各是什么?
(2)12时,水位是多少?
(3)哪一时段水位上升最快?
4.下表是小华做观察水的沸腾实验时所记录的数据:
(1)时间是8分钟时,水的温度为_____;
(2)此表反映了变量_____和_____之间的关系,其中_____是自变量,_____是因变量;
(3)在_____时间内,温度随时间增加而增加;_____时间内,水的温度不再变化.
单击此处添加标题
文字内容
0
10
20
30
40
50
60
70
80
文字内容
文字内容
文字内容
文字内容
文字内容
文字内容
文字内容
文字内容
36
41
45
57
54
39
48
60
5.某电影院地面的一部分是扇形,座位按下列方式设置:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}排数
1
2
3
4
座位数
60
64
68
72
(1)上述哪些量在变化?自变量和因变量分别是什么?
(2)第5排、第6排各有多少个座位?
(3)第n排有多少个座位?请说明你的理由。
6.某电信公司提供了一种移动通讯服务的收费标准,如下表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}项目
月基本服务费
月免费通话时间
超出后每分收费
标准
40元
150分
0.6元
(1)上述哪些量在变化?自变量和因变量分别是什么?
(2)第5排、第6排各有多少个座位?
(3)第n排有多少个座位?请说明你的理由。
6.研究发现,地表以下岩层的温度与它所处的深度有表中的关系:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}岩层的深度h/km
1
2
3
4
5
6
…
岩层的温度t/℃
55
90
125
160
195
230
…
根据以上信息,回答下列问题:
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)岩层的深度h每增加1km,温度t是怎样变化的?
(3)估计岩层10km深处的温度是多少?
8.阅读下面这段有关“龟兔赛跑”的寓言故事,并指出所涉及的量中,哪些是常量,哪些是变量.
一次乌龟与兔子举行500米赛跑,比赛开始不久,兔子就遥遥领先.当兔子以20米/分的速度跑了10分时,往回一看,乌龟远远地落在后面呢!兔子心想:“我就是睡一觉,你乌龟也追不上我,我为何不在此美美地睡上一觉呢?”可是,当骄傲的兔子正做着胜利者的美梦时,勤勉的乌龟却从它身边悄悄爬过,并以10米/分的速度匀速爬向终点.40分后,兔子梦醒了,而此时乌龟刚好到达终点.兔子悔之晚矣,等它再以30米/分的速度跑向终点时,它比乌龟足足晚了10分.
谢谢观看
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
