北师大版七年级下册4.3探索三角形全等的条件 --两边和一角课件(共30张PPT)
文档属性
| 名称 | 北师大版七年级下册4.3探索三角形全等的条件 --两边和一角课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-03 00:00:00 | ||
图片预览




文档简介
利用“两边一角”判定三角形全等
第四章 三角形
教学目标
1.掌握三角形全等的“SAS”判定;(重点)
2.能运用“SAS ”说明简单的三角形全等问题; (难点)
3.判定三角形全等的灵活运用
学习指南
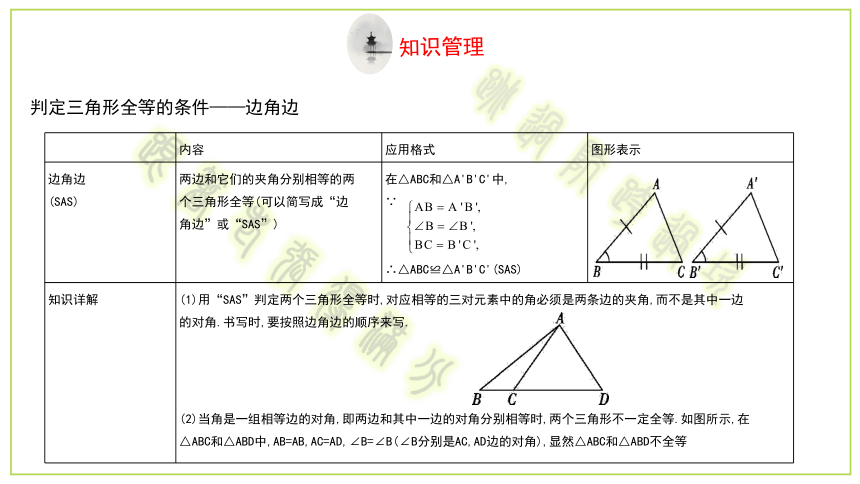
?判定三角形全等的条件——边角边
内容
应用格式
图形表示
边角边
(SAS)
两边和它们的夹角分别相等的两
个三角形全等(可以简写成“边
角边”或“SAS”)
在△ABC和△A'B'C'中,
∵?
∴△ABC≌△A'B'C'(SAS)
?
知识详解
(1)用“SAS”判定两个三角形全等时,对应相等的三对元素中的角必须是两条边的夹角,而不是其中一边
的对角.书写时,要按照边角边的顺序来写.
?
(2)当角是一组相等边的对角,即两边和其中一边的对角分别相等时,两个三角形不一定全等.如图所示,在
△ABC和△ABD中,AB=AB,AC=AD,∠B=∠B(∠B分别是AC,AD边的对角),显然△ABC和△ABD不全等
知识管理
全等三角形判定方法的灵活运用
判定两个三角形全等时,如果给出的条件不全面,则需要根据已知的条件结合相应的判定方法进行分析,先找出所缺的条件再说明全等.
具体思路如下:
知识管理
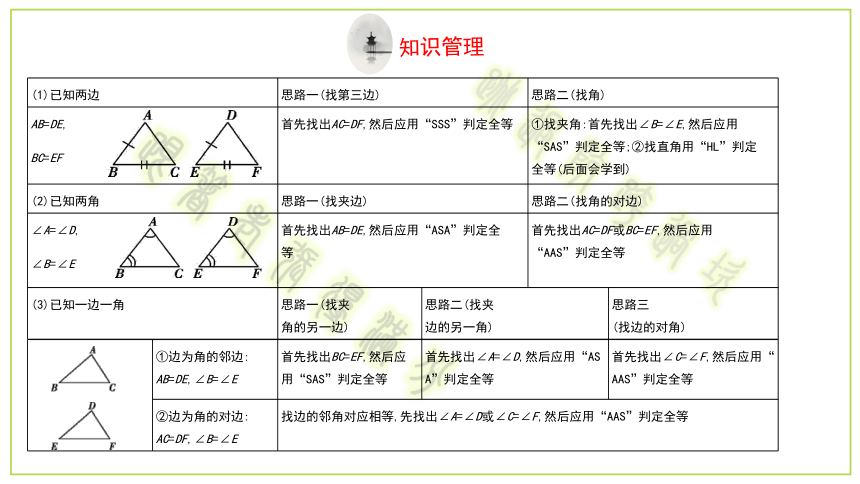
(1)已知两边
思路一(找第三边)
思路二(找角)
AB=DE,
BC=EF
首先找出AC=DF,然后应用“SSS”判定全等
①找夹角:首先找出∠B=∠E,然后应用
“SAS”判定全等;②找直角用“HL”判定
全等(后面会学到)
(2)已知两角
思路一(找夹边)
思路二(找角的对边)
∠A=∠D,
∠B=∠E
首先找出AB=DE,然后应用“ASA”判定全
等
首先找出AC=DF或BC=EF,然后应用
“AAS”判定全等
(3)已知一边一角
思路一(找夹
角的另一边)
思路二(找夹
边的另一角)
思路三
(找边的对角)
?
①边为角的邻边:
AB=DE,∠B=∠E
首先找出BC=EF,然后应用“SAS”判定全等
首先找出∠A=∠D,然后应用“ASA”判定全等
首先找出∠C=∠F,然后应用“AAS”判定全等
②边为角的对边:
AC=DF,∠B=∠E
找边的邻角对应相等,先找出∠A=∠D或∠C=∠F,然后应用“AAS”判定全等
知识管理
根据探索三角形全等的条件,至少需要三个条件,除了上述三种情况外,还有哪种情况?
两边一角相等
1.两边及夹角;
2.两边及其一边的对角.
类型一:利用“SAS”判定三角形全等
归类探究
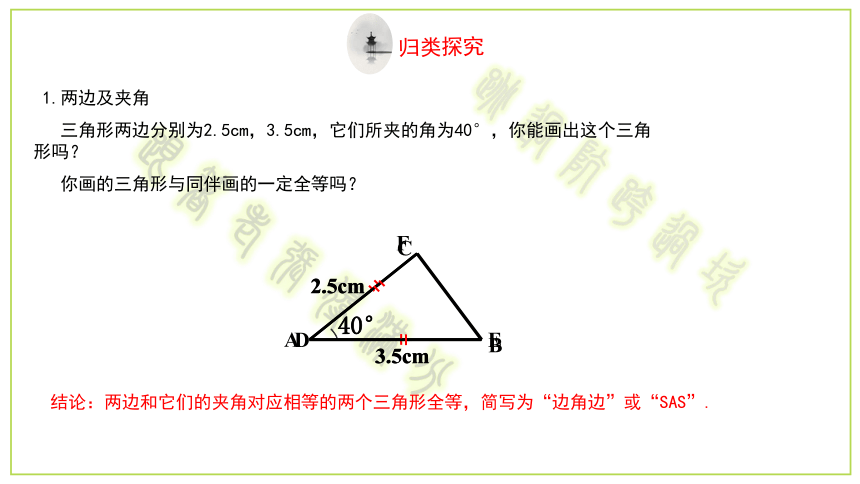
1.两边及夹角
三角形两边分别为2.5cm,3.5cm,它们所夹的角为40°,你能画出这个三角形吗?
你画的三角形与同伴画的一定全等吗?
3.5cm
2.5cm
40°
A
B
C
3.5cm
2.5cm
40°
D
E
F
结论:两边和它们的夹角对应相等的两个三角形全等,简写为“边角边”或“SAS”.
归类探究
B
C
A
2.5cm
3.5cm
40°
E
D
F
40°
3.5cm
2.5cm
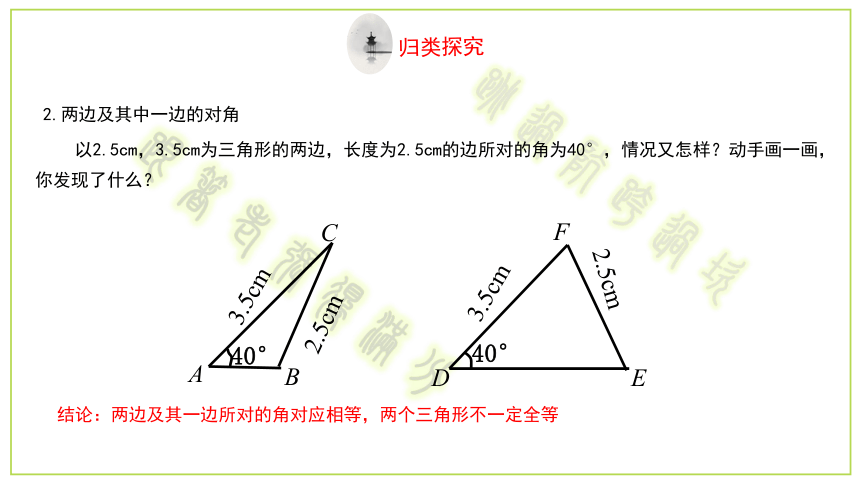
以2.5cm,3.5cm为三角形的两边,长度为2.5cm的边所对的角为40°,情况又怎样?动手画一画,你发现了什么?
2.两边及其中一边的对角
结论:两边及其一边所对的角对应相等,两个三角形不一定全等
归类探究
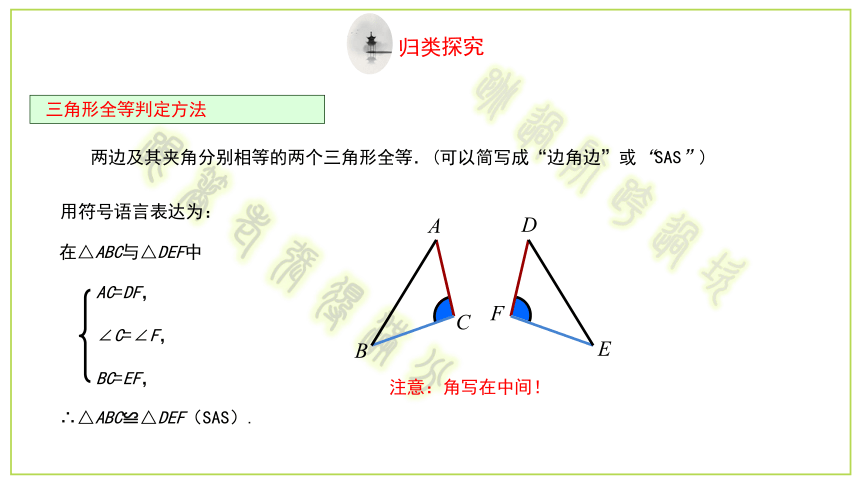
三角形全等判定方法
用符号语言表达为:
在△ABC与△DEF中
∴△ABC≌△DEF(SAS).
两边及其夹角分别相等的两个三角形全等.(可以简写成“边角边”或“SAS”)
F
E
D
C
B
A
AC=DF,
∠C=∠F,
BC=EF,
注意:角写在中间!
归类探究
4
4
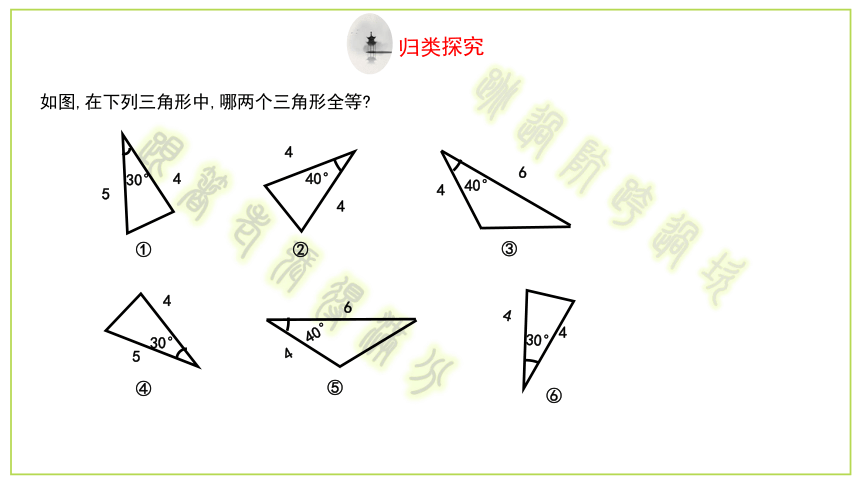
如图,在下列三角形中,哪两个三角形全等?
4
4
5
5
30°
30°
4
4
30°
4
6
40°
4
6
40°
40°
①
③
②
⑥
⑤
④
归类探究
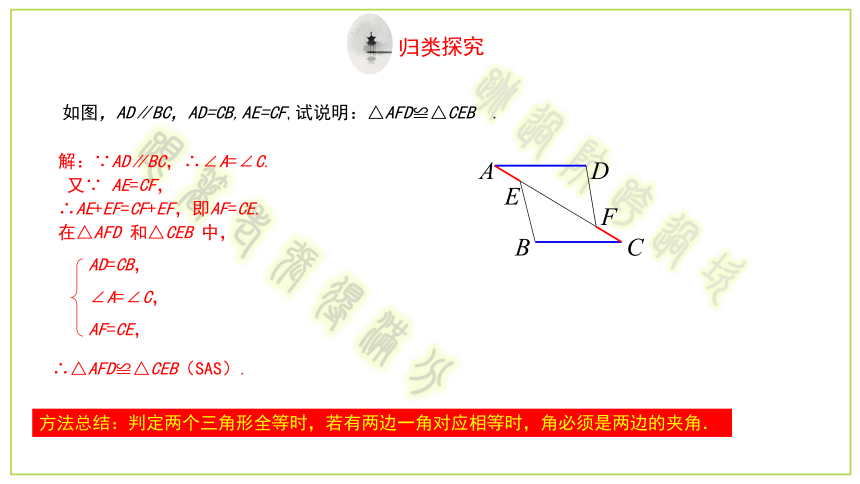
解:∵AD∥BC,∴∠A=∠C.
又∵ AE=CF,
∴AE+EF=CF+EF,即AF=CE.
在△AFD 和△CEB 中,
AD=CB,
∠A=∠C,
AF=CE,
A
D
B
E
F
C
如图,AD∥BC,AD=CB,AE=CF,试说明:△AFD≌△CEB .
∴△AFD≌△CEB(SAS).
方法总结:判定两个三角形全等时,若有两边一角对应相等时,角必须是两边的夹角.
归类探究
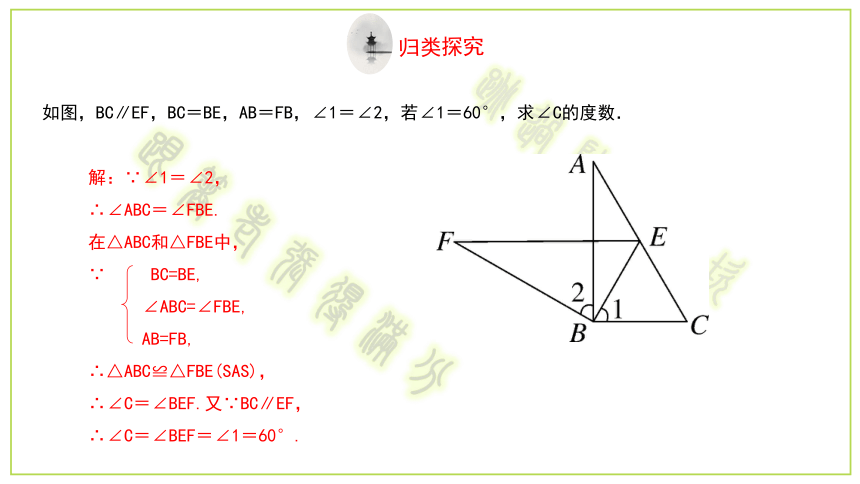
如图,BC∥EF,BC=BE,AB=FB,∠1=∠2,若∠1=60°,求∠C的度数.
解:∵∠1=∠2,
∴∠ABC=∠FBE.
在△ABC和△FBE中,
∵ BC=BE,
∠ABC=∠FBE,
AB=FB,
∴△ABC≌△FBE(SAS),
∴∠C=∠BEF.又∵BC∥EF,
∴∠C=∠BEF=∠1=60°.
归类探究
1.下列图形中有没有全等三角形,并说明全等的理由.
甲
8 cm
9 cm
丙
8 cm
9 cm
8 cm
9 cm
乙
30°
30°
30°
甲与丙全等,SAS.
当堂测评
2.在下列推理中填写需要补充的条件,使结论成立.
(已知),
=
∠A=∠A(公共角),
=
C
B
∴△AEC≌△ADB ( ).
在△AEC和△ADB中,
AB
AC
AD
AE
A
D
E
SAS
注意:“SAS”中的角必须是两边的夹角,“A”必须在中间.
.
当堂测评
3.如图,AC=BD,∠CAB= ∠DBA,试说明:BC=AD.
A
B
C
D
解:在△ABC与△BAD中,
∴△ABC≌△BAD(SAS),
AC=BD,
∠CAB=∠DBA,
AB=BA,
∴BC=AD
(全等三角形的对应边相等).
当堂测评
B
C
D
E
A
4.如图,已知AB=AC,AD=AE,试说明:∠B=∠C.
C
E
A
B
A
D
解:在△ABD和△ACE中,
∴△ABD≌△ACE(SAS)
∴∠B=∠C(全等三角形
对应角相等).
AB=AC(已知),
∠A=∠A(公共角),
AD=AE(已知),
当堂测评
5.小兰做了一个如图所示的风筝,其中∠EDH=∠FDH, ED=FD ,将上述条件标注在图中,小明不用测量就能知道EH=FH吗?
E
F
D
H
解:能.在△EDH和△FDH中 ,
ED=FD(已知),
∠EDH=∠FDH(已知),
DH=DH(公共边),
∴△EDH≌△FDH(SAS),
∴EH=FH.(全等三角形对应边相等).
当堂测评
6.已知:如图,AB=DB,CB=EB,∠1=∠2, 试说明:∠A=∠D.
解:∵ ∠1=∠2(已知),
∴∠1+∠DBC= ∠2+ ∠DBC,
即∠ABC=∠DBE.
在△ABC和△DBE中,
AB=DB(已知),
∠ABC=∠DBE(已证),
CB=EB(已知),
∴△ABC≌△DBE(SAS).
∴ ∠A=∠D(全等三角形的对应角相等).
1
A
2
C
B
D
E
当堂测评
7.如图,在湖泊的岸边有A、B两点,难以直接量出A、B两点间的距离.你能设计一种量出A、B两点之间距离的方案吗?
OA=OD,∠AOB=∠DOE,OB=OE,
∴△ABO≌△DEO(SAS).
∴AB=DE.
当堂测评
边角边
内容
有两边及夹角对应相等的两个
三角形全等(简写成 “SAS”)
应用
为证明线段和角相等提供了新的证法
注意
1.已知两边,必须找“夹角”;
2.已知一角和这角的一夹边,必须找这角的另一夹边.
课堂小结
(2019 辽宁大连)如图,点E,F在BC上,BE=CF,AB=DC,∠B=∠C, 求证:AF=DE
拓展提升
如图,在△ABC和△DAE中,∠BAC=∠DAE,AB=AE,AC=AD,连接BD,CE。求证:BD=CE.
拓展提升
如图,点C为AB的中点,CD=BE,CD∥BE。试说明:△ACD≌△CBE
拓展提升
如图,D、E、F、B在同一条直线上,AB=CD,∠B=∠D,BF=DE。试说明:
(1)AE=CF
(2)AE∥CF
拓展提升
如图,AC=AE,∠1=∠2,AB=AD,试说明:BC=DE
拓展提升
如图,C为BE上的一点,点A、D分别在BE两侧,AB∥ED,AB=CE,BC=ED。试说明:AC=CD
拓展提升
如图,已知点B、E、C、F在一条直线上,AB=DF,AC=DE,∠A=∠D。
(1)试说明:AC∥DE;
(2)若BF=13,EC=5,求BC的长。
拓展提升
如图,在四边形ABCD中,AB=AD,BC=DC,E为线段AC上的一动点(不与点A重合),在点E的移动过程中,BE和DE是否相等?并说明理由。
拓展提升
?(2017四川南充中考)如图,DE⊥AB,CF⊥AB,垂足分别是点E、F,DE=CF,AE=BF,
试说明:AC∥BD.
归类探究
第四章 三角形
教学目标
1.掌握三角形全等的“SAS”判定;(重点)
2.能运用“SAS ”说明简单的三角形全等问题; (难点)
3.判定三角形全等的灵活运用
学习指南
?判定三角形全等的条件——边角边
内容
应用格式
图形表示
边角边
(SAS)
两边和它们的夹角分别相等的两
个三角形全等(可以简写成“边
角边”或“SAS”)
在△ABC和△A'B'C'中,
∵?
∴△ABC≌△A'B'C'(SAS)
?
知识详解
(1)用“SAS”判定两个三角形全等时,对应相等的三对元素中的角必须是两条边的夹角,而不是其中一边
的对角.书写时,要按照边角边的顺序来写.
?
(2)当角是一组相等边的对角,即两边和其中一边的对角分别相等时,两个三角形不一定全等.如图所示,在
△ABC和△ABD中,AB=AB,AC=AD,∠B=∠B(∠B分别是AC,AD边的对角),显然△ABC和△ABD不全等
知识管理
全等三角形判定方法的灵活运用
判定两个三角形全等时,如果给出的条件不全面,则需要根据已知的条件结合相应的判定方法进行分析,先找出所缺的条件再说明全等.
具体思路如下:
知识管理
(1)已知两边
思路一(找第三边)
思路二(找角)
AB=DE,
BC=EF
首先找出AC=DF,然后应用“SSS”判定全等
①找夹角:首先找出∠B=∠E,然后应用
“SAS”判定全等;②找直角用“HL”判定
全等(后面会学到)
(2)已知两角
思路一(找夹边)
思路二(找角的对边)
∠A=∠D,
∠B=∠E
首先找出AB=DE,然后应用“ASA”判定全
等
首先找出AC=DF或BC=EF,然后应用
“AAS”判定全等
(3)已知一边一角
思路一(找夹
角的另一边)
思路二(找夹
边的另一角)
思路三
(找边的对角)
?
①边为角的邻边:
AB=DE,∠B=∠E
首先找出BC=EF,然后应用“SAS”判定全等
首先找出∠A=∠D,然后应用“ASA”判定全等
首先找出∠C=∠F,然后应用“AAS”判定全等
②边为角的对边:
AC=DF,∠B=∠E
找边的邻角对应相等,先找出∠A=∠D或∠C=∠F,然后应用“AAS”判定全等
知识管理
根据探索三角形全等的条件,至少需要三个条件,除了上述三种情况外,还有哪种情况?
两边一角相等
1.两边及夹角;
2.两边及其一边的对角.
类型一:利用“SAS”判定三角形全等
归类探究
1.两边及夹角
三角形两边分别为2.5cm,3.5cm,它们所夹的角为40°,你能画出这个三角形吗?
你画的三角形与同伴画的一定全等吗?
3.5cm
2.5cm
40°
A
B
C
3.5cm
2.5cm
40°
D
E
F
结论:两边和它们的夹角对应相等的两个三角形全等,简写为“边角边”或“SAS”.
归类探究
B
C
A
2.5cm
3.5cm
40°
E
D
F
40°
3.5cm
2.5cm
以2.5cm,3.5cm为三角形的两边,长度为2.5cm的边所对的角为40°,情况又怎样?动手画一画,你发现了什么?
2.两边及其中一边的对角
结论:两边及其一边所对的角对应相等,两个三角形不一定全等
归类探究
三角形全等判定方法
用符号语言表达为:
在△ABC与△DEF中
∴△ABC≌△DEF(SAS).
两边及其夹角分别相等的两个三角形全等.(可以简写成“边角边”或“SAS”)
F
E
D
C
B
A
AC=DF,
∠C=∠F,
BC=EF,
注意:角写在中间!
归类探究
4
4
如图,在下列三角形中,哪两个三角形全等?
4
4
5
5
30°
30°
4
4
30°
4
6
40°
4
6
40°
40°
①
③
②
⑥
⑤
④
归类探究
解:∵AD∥BC,∴∠A=∠C.
又∵ AE=CF,
∴AE+EF=CF+EF,即AF=CE.
在△AFD 和△CEB 中,
AD=CB,
∠A=∠C,
AF=CE,
A
D
B
E
F
C
如图,AD∥BC,AD=CB,AE=CF,试说明:△AFD≌△CEB .
∴△AFD≌△CEB(SAS).
方法总结:判定两个三角形全等时,若有两边一角对应相等时,角必须是两边的夹角.
归类探究
如图,BC∥EF,BC=BE,AB=FB,∠1=∠2,若∠1=60°,求∠C的度数.
解:∵∠1=∠2,
∴∠ABC=∠FBE.
在△ABC和△FBE中,
∵ BC=BE,
∠ABC=∠FBE,
AB=FB,
∴△ABC≌△FBE(SAS),
∴∠C=∠BEF.又∵BC∥EF,
∴∠C=∠BEF=∠1=60°.
归类探究
1.下列图形中有没有全等三角形,并说明全等的理由.
甲
8 cm
9 cm
丙
8 cm
9 cm
8 cm
9 cm
乙
30°
30°
30°
甲与丙全等,SAS.
当堂测评
2.在下列推理中填写需要补充的条件,使结论成立.
(已知),
=
∠A=∠A(公共角),
=
C
B
∴△AEC≌△ADB ( ).
在△AEC和△ADB中,
AB
AC
AD
AE
A
D
E
SAS
注意:“SAS”中的角必须是两边的夹角,“A”必须在中间.
.
当堂测评
3.如图,AC=BD,∠CAB= ∠DBA,试说明:BC=AD.
A
B
C
D
解:在△ABC与△BAD中,
∴△ABC≌△BAD(SAS),
AC=BD,
∠CAB=∠DBA,
AB=BA,
∴BC=AD
(全等三角形的对应边相等).
当堂测评
B
C
D
E
A
4.如图,已知AB=AC,AD=AE,试说明:∠B=∠C.
C
E
A
B
A
D
解:在△ABD和△ACE中,
∴△ABD≌△ACE(SAS)
∴∠B=∠C(全等三角形
对应角相等).
AB=AC(已知),
∠A=∠A(公共角),
AD=AE(已知),
当堂测评
5.小兰做了一个如图所示的风筝,其中∠EDH=∠FDH, ED=FD ,将上述条件标注在图中,小明不用测量就能知道EH=FH吗?
E
F
D
H
解:能.在△EDH和△FDH中 ,
ED=FD(已知),
∠EDH=∠FDH(已知),
DH=DH(公共边),
∴△EDH≌△FDH(SAS),
∴EH=FH.(全等三角形对应边相等).
当堂测评
6.已知:如图,AB=DB,CB=EB,∠1=∠2, 试说明:∠A=∠D.
解:∵ ∠1=∠2(已知),
∴∠1+∠DBC= ∠2+ ∠DBC,
即∠ABC=∠DBE.
在△ABC和△DBE中,
AB=DB(已知),
∠ABC=∠DBE(已证),
CB=EB(已知),
∴△ABC≌△DBE(SAS).
∴ ∠A=∠D(全等三角形的对应角相等).
1
A
2
C
B
D
E
当堂测评
7.如图,在湖泊的岸边有A、B两点,难以直接量出A、B两点间的距离.你能设计一种量出A、B两点之间距离的方案吗?
OA=OD,∠AOB=∠DOE,OB=OE,
∴△ABO≌△DEO(SAS).
∴AB=DE.
当堂测评
边角边
内容
有两边及夹角对应相等的两个
三角形全等(简写成 “SAS”)
应用
为证明线段和角相等提供了新的证法
注意
1.已知两边,必须找“夹角”;
2.已知一角和这角的一夹边,必须找这角的另一夹边.
课堂小结
(2019 辽宁大连)如图,点E,F在BC上,BE=CF,AB=DC,∠B=∠C, 求证:AF=DE
拓展提升
如图,在△ABC和△DAE中,∠BAC=∠DAE,AB=AE,AC=AD,连接BD,CE。求证:BD=CE.
拓展提升
如图,点C为AB的中点,CD=BE,CD∥BE。试说明:△ACD≌△CBE
拓展提升
如图,D、E、F、B在同一条直线上,AB=CD,∠B=∠D,BF=DE。试说明:
(1)AE=CF
(2)AE∥CF
拓展提升
如图,AC=AE,∠1=∠2,AB=AD,试说明:BC=DE
拓展提升
如图,C为BE上的一点,点A、D分别在BE两侧,AB∥ED,AB=CE,BC=ED。试说明:AC=CD
拓展提升
如图,已知点B、E、C、F在一条直线上,AB=DF,AC=DE,∠A=∠D。
(1)试说明:AC∥DE;
(2)若BF=13,EC=5,求BC的长。
拓展提升
如图,在四边形ABCD中,AB=AD,BC=DC,E为线段AC上的一动点(不与点A重合),在点E的移动过程中,BE和DE是否相等?并说明理由。
拓展提升
?(2017四川南充中考)如图,DE⊥AB,CF⊥AB,垂足分别是点E、F,DE=CF,AE=BF,
试说明:AC∥BD.
归类探究
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
