北师大版七年级下册数学:2.1 对顶角、余角和补角 课件(共26张PPT)
文档属性
| 名称 | 北师大版七年级下册数学:2.1 对顶角、余角和补角 课件(共26张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-03 14:57:43 | ||
图片预览





文档简介
2.1
北师大版七年级下册
生活中不是缺少数学,而是缺少发现数学的眼睛!数学,就在我们身边!
观察下列图形,你能发现哪些数学现象和数学问题?
在同一平面内,两条直线的位置关系有相交和平行两种
在同一平面内,不相交的两条直线叫平行线。
生活中处处可见在大自然的杰作和人类的创造物中,蕴含着无数的相交线和平行线。我们知道:
在同一平面内,有一个公共点的两条直线叫相交线。
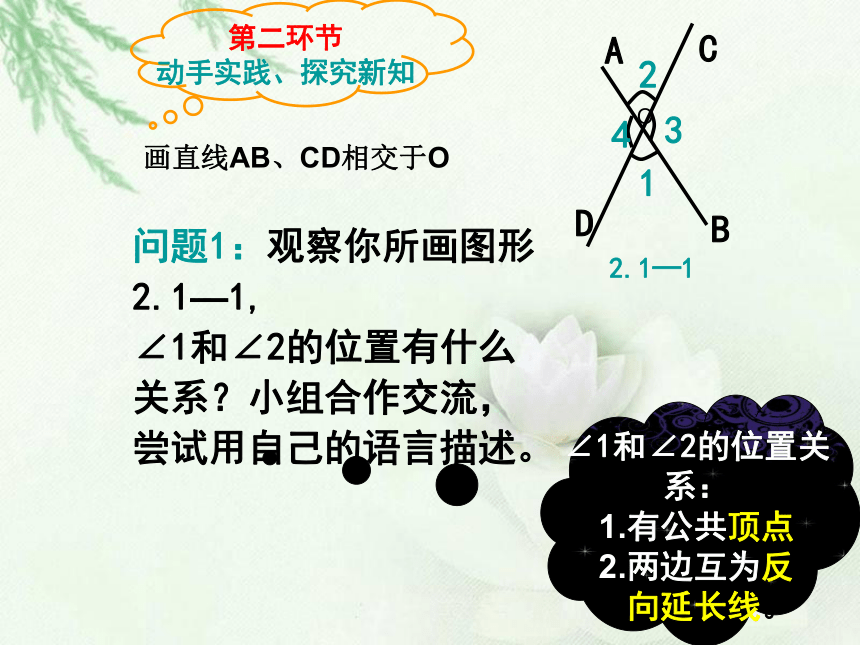
∠1和∠2的位置关系:
1.有公共顶点
2.两边互为反
向延长线。
问题1:观察你所画图形2.1—1,
∠1和∠2的位置有什么关系?小组合作交流,尝试用自己的语言描述。
3
2
1
4
2.1─1
A
B
C
D
第二环节
动手实践、探究新知
O
画直线AB、CD相交于O
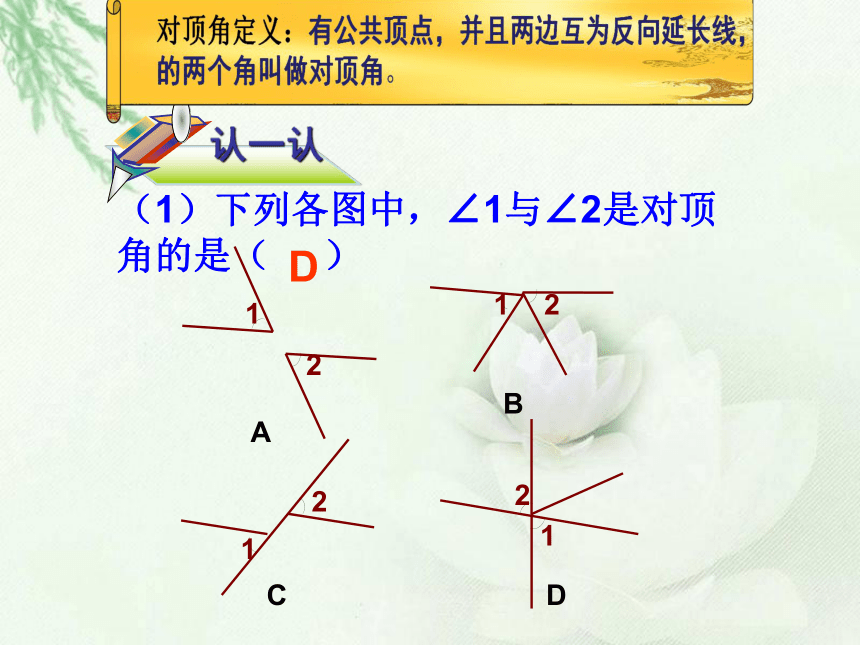
归纳总结
直线AB与CD相交于点O,∠1与∠2有公共顶点O,它们的两边互为反向延长线,这样的两个角叫做对顶角
(1)下列各图中,∠1与∠2是对顶角的是( )
1
2
C
1
2
D
D
1
2
A
1
2
B
认一认
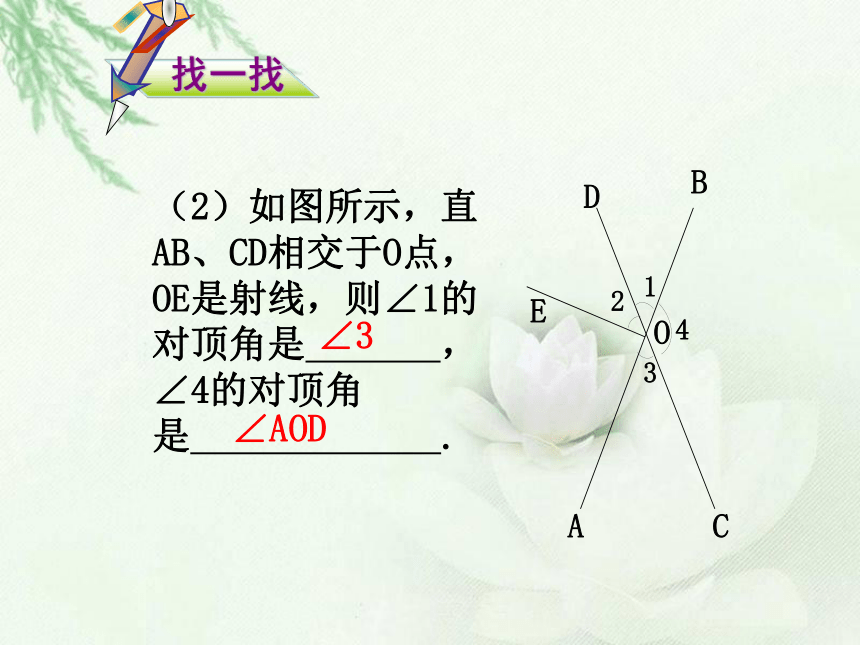
(2)如图所示,直AB、CD相交于O点,OE是射线,则∠1的对顶角是 ,∠4的对顶角是 .
∠AOD
∠3
O
2
1
3
4
E
B
A
C
D
找一找
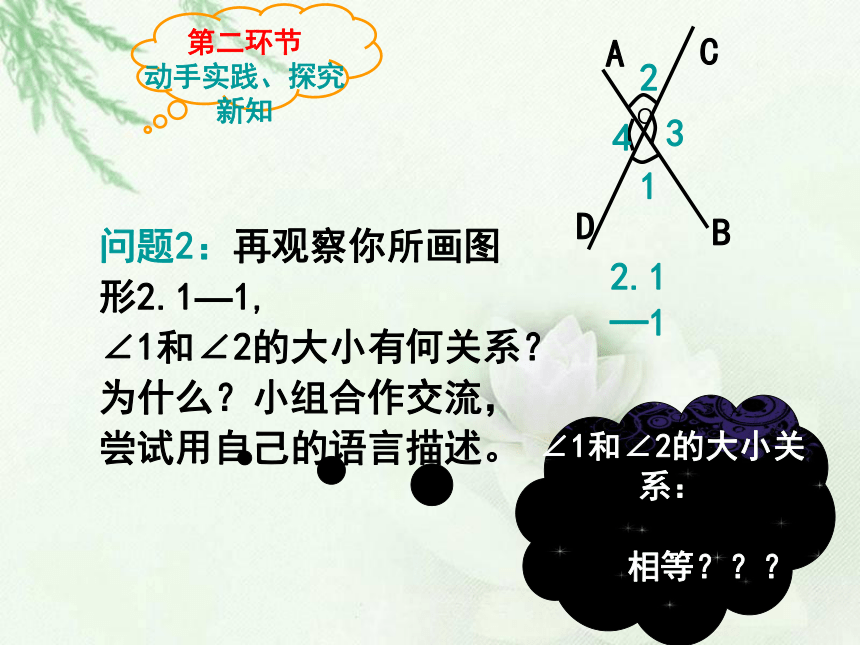
∠1和∠2的大小关系:
。
相等???
问题2:再观察你所画图形2.1—1,
∠1和∠2的大小有何关系?为什么?小组合作交流,尝试用自己的语言描述。
3
2
1
4
2.1─1
A
B
C
D
第二环节
动手实践、探究新知
O
已知:如图,直线AB与CD交于O.
试说明:∠1=∠2
推理探究对顶角的大小关系:
A
B
D
C
O
1(
)2
∵∠1 +∠AOC =180°(平角定义)
∠2 +∠AOC =180°(平角定义)
∴∠1 = ∠2
∴∠1 =180°-∠AOC
∴∠2 =180°-∠AOC
归纳总结
有公共顶点,两边互为反向延长线的两个角叫做对顶角(vertical angles) 。
对顶角相等
3.如图所示,有一个破损的扇形零件,利用图中的量角器可以量出这个扇形零件的圆心角的度数吗?你能说出所量角的度数是多少吗?为什么?
应用举例
(4)如图,已知AB、CD、EF是相交于点O的直线,∠DOE=90°.如果∠AOC=70°,那么∠BOF等于多少度?为什么?
算一算
∵∠AOC=70°(已知)
∴∠BOD=70°(对顶角相等)
∵∠DOE=90°(已知)
∴∠DOF=90°(平角定义)
∴∠BOF=∠DOF-∠DOB
=90°- 70°=20°
(4)如图,已知AB、CD、EF是相交于点O的直线,∠DOE=90°.如果∠AOC=70°,还可以求出哪些角?
算一算
∠AOC=70°
∠BOD=70°
∠DOE=∠COF=90°
∠DOF=∠COE=90°
∠BOF=∠AOE=20°
∠BOC=∠AOD=110°
∠AOF=∠BOE=160°
(1)定义中的“互为”一词如何理解?
(3)互补、互余的两角是否一定有公共顶点或公共边?
(2)∠1 + ∠2 + ∠3 = 180°,能说∠1 、∠2、 ∠3 互补吗?
三、余角和补角的定义
1、定义:
如果两个角的和等于90?,那么这两个角叫做互为余角.简称这两个角互余.
如果两个角的和等于180?,那么这两个角叫做互为补角.简称这两个角互补.
2、问题:
(4)如图,已知AB、CD、EF是相交于点O的直线,∠DOE=90°.如果∠AOC=70°,那么,你能找到互余的角、互补的角吗?
算一算
∠α的补角
5°
77°
62°23′
x °
练习1:
85°
13°
27°37′
90°-x °
175°
103°
117°37′
180°-x °
2.同一个锐角的补角比它的余角大多少?
=90°
(180-x)o
思考:
1.锐角是否都有余角和补角?钝角呢?
(90-x)o
-
∠α
∠α的余角
∠α
∠α的余角
∠α的补角
5°
77°
62°23′
x °
练习1:
85°
13°
27°37′
90°-x °
95°
145°
175°
103°
117°37′
180°-x °
85°
35°
不存在
不存在
同一个锐角的补角比它的余角大多少?
=90°
互余和互补是两个角的数量关系,与它们的位置无关.
(180o-xo)-(90o-xo)
练习2:
若一个角的补角等于它的余角的4倍,求这个角的度数.
解:设这个角是x°则它的补角是(180-x)°, 余角是(90-x)° ,根据题意得:
180-x = 4(90-x)
解得: x = 60
答:这个角的度数是60°.
如果∠1+∠3=90?
∠2+∠3=90?
那么∠1=
∠2=
所以:∠1=∠2
如果∠3= ∠4,并且:
∠1+∠3=90?
∠2+∠4=90?
那么∠1= 90?-∠3
∠2= 90?-∠4= 90?-∠3
所以 ∠1= ∠2
90?-∠3
90?-∠3
由此,你有什么收获?
同角 的余角相等
(等角)
同角 的补角相等
(等角 )
如果把上面的90?改为180?,你又会发现什么?
1)若∠1与∠2互余, ∠2与∠3互余,则 ___________,根据___________.
2)若∠1与∠2互补, ∠2与∠3互补,则___________,根据___________.
∠1= ∠3
同角的余角相等
∠1= ∠3
同角的补角相等
巩固练习1
互补的角
∠2=∠4 , ∠AOC=∠BOC=∠DOE=90° ∠1=∠3
互余的角
相等的角
∠1与∠2、∠1与∠4;∠3与∠2、∠3与∠4;
∠AOE与∠4,∠AOE与∠2;
∠DOB与∠1、∠DOB与∠3;
C
A
O
B
D
E
)
)
(
)
4
3
1
2
如图A、O、 B在同一直线上,∠AOC= ∠DOE= 90°,找出图中:
巩固练习2
∠AOC、∠BOC、∠DOE两两互补
课堂总结:
反思本节课学到了什么?
你还有哪些疑问?
A
D
C
B
O
认真观察这幅图片,你能发现什么?
我们的幸福美好生活是亿万劳动者
撸起袖子加油干而努力奋斗出来的!
感谢他们!
如图1-2-3,已知∠AOC与∠BOD都是直角,∠BOC=60°.
(1)求∠AOB和∠DOC的度数;
(2)∠A OB与∠DOC有何大小关系;
(3)若不知道∠BOC的具体度数,其他条件不变,这种关系仍然成立吗?请说明理由.
作业与思考1.
(1)如图①,△ABC中,∠C=90°.则∠A是∠B的 。
(2)变式训练:在①的基础上,作∠CDA=900,如图②.
1.则∠A的余角有哪几个?为什么?
2.请找出图中相等的角,并说明理由.
作业与思考2.
C
A
B
C
A
B
D
图①
图②
2
1
北师大版七年级下册
生活中不是缺少数学,而是缺少发现数学的眼睛!数学,就在我们身边!
观察下列图形,你能发现哪些数学现象和数学问题?
在同一平面内,两条直线的位置关系有相交和平行两种
在同一平面内,不相交的两条直线叫平行线。
生活中处处可见在大自然的杰作和人类的创造物中,蕴含着无数的相交线和平行线。我们知道:
在同一平面内,有一个公共点的两条直线叫相交线。
∠1和∠2的位置关系:
1.有公共顶点
2.两边互为反
向延长线。
问题1:观察你所画图形2.1—1,
∠1和∠2的位置有什么关系?小组合作交流,尝试用自己的语言描述。
3
2
1
4
2.1─1
A
B
C
D
第二环节
动手实践、探究新知
O
画直线AB、CD相交于O
归纳总结
直线AB与CD相交于点O,∠1与∠2有公共顶点O,它们的两边互为反向延长线,这样的两个角叫做对顶角
(1)下列各图中,∠1与∠2是对顶角的是( )
1
2
C
1
2
D
D
1
2
A
1
2
B
认一认
(2)如图所示,直AB、CD相交于O点,OE是射线,则∠1的对顶角是 ,∠4的对顶角是 .
∠AOD
∠3
O
2
1
3
4
E
B
A
C
D
找一找
∠1和∠2的大小关系:
。
相等???
问题2:再观察你所画图形2.1—1,
∠1和∠2的大小有何关系?为什么?小组合作交流,尝试用自己的语言描述。
3
2
1
4
2.1─1
A
B
C
D
第二环节
动手实践、探究新知
O
已知:如图,直线AB与CD交于O.
试说明:∠1=∠2
推理探究对顶角的大小关系:
A
B
D
C
O
1(
)2
∵∠1 +∠AOC =180°(平角定义)
∠2 +∠AOC =180°(平角定义)
∴∠1 = ∠2
∴∠1 =180°-∠AOC
∴∠2 =180°-∠AOC
归纳总结
有公共顶点,两边互为反向延长线的两个角叫做对顶角(vertical angles) 。
对顶角相等
3.如图所示,有一个破损的扇形零件,利用图中的量角器可以量出这个扇形零件的圆心角的度数吗?你能说出所量角的度数是多少吗?为什么?
应用举例
(4)如图,已知AB、CD、EF是相交于点O的直线,∠DOE=90°.如果∠AOC=70°,那么∠BOF等于多少度?为什么?
算一算
∵∠AOC=70°(已知)
∴∠BOD=70°(对顶角相等)
∵∠DOE=90°(已知)
∴∠DOF=90°(平角定义)
∴∠BOF=∠DOF-∠DOB
=90°- 70°=20°
(4)如图,已知AB、CD、EF是相交于点O的直线,∠DOE=90°.如果∠AOC=70°,还可以求出哪些角?
算一算
∠AOC=70°
∠BOD=70°
∠DOE=∠COF=90°
∠DOF=∠COE=90°
∠BOF=∠AOE=20°
∠BOC=∠AOD=110°
∠AOF=∠BOE=160°
(1)定义中的“互为”一词如何理解?
(3)互补、互余的两角是否一定有公共顶点或公共边?
(2)∠1 + ∠2 + ∠3 = 180°,能说∠1 、∠2、 ∠3 互补吗?
三、余角和补角的定义
1、定义:
如果两个角的和等于90?,那么这两个角叫做互为余角.简称这两个角互余.
如果两个角的和等于180?,那么这两个角叫做互为补角.简称这两个角互补.
2、问题:
(4)如图,已知AB、CD、EF是相交于点O的直线,∠DOE=90°.如果∠AOC=70°,那么,你能找到互余的角、互补的角吗?
算一算
∠α的补角
5°
77°
62°23′
x °
练习1:
85°
13°
27°37′
90°-x °
175°
103°
117°37′
180°-x °
2.同一个锐角的补角比它的余角大多少?
=90°
(180-x)o
思考:
1.锐角是否都有余角和补角?钝角呢?
(90-x)o
-
∠α
∠α的余角
∠α
∠α的余角
∠α的补角
5°
77°
62°23′
x °
练习1:
85°
13°
27°37′
90°-x °
95°
145°
175°
103°
117°37′
180°-x °
85°
35°
不存在
不存在
同一个锐角的补角比它的余角大多少?
=90°
互余和互补是两个角的数量关系,与它们的位置无关.
(180o-xo)-(90o-xo)
练习2:
若一个角的补角等于它的余角的4倍,求这个角的度数.
解:设这个角是x°则它的补角是(180-x)°, 余角是(90-x)° ,根据题意得:
180-x = 4(90-x)
解得: x = 60
答:这个角的度数是60°.
如果∠1+∠3=90?
∠2+∠3=90?
那么∠1=
∠2=
所以:∠1=∠2
如果∠3= ∠4,并且:
∠1+∠3=90?
∠2+∠4=90?
那么∠1= 90?-∠3
∠2= 90?-∠4= 90?-∠3
所以 ∠1= ∠2
90?-∠3
90?-∠3
由此,你有什么收获?
同角 的余角相等
(等角)
同角 的补角相等
(等角 )
如果把上面的90?改为180?,你又会发现什么?
1)若∠1与∠2互余, ∠2与∠3互余,则 ___________,根据___________.
2)若∠1与∠2互补, ∠2与∠3互补,则___________,根据___________.
∠1= ∠3
同角的余角相等
∠1= ∠3
同角的补角相等
巩固练习1
互补的角
∠2=∠4 , ∠AOC=∠BOC=∠DOE=90° ∠1=∠3
互余的角
相等的角
∠1与∠2、∠1与∠4;∠3与∠2、∠3与∠4;
∠AOE与∠4,∠AOE与∠2;
∠DOB与∠1、∠DOB与∠3;
C
A
O
B
D
E
)
)
(
)
4
3
1
2
如图A、O、 B在同一直线上,∠AOC= ∠DOE= 90°,找出图中:
巩固练习2
∠AOC、∠BOC、∠DOE两两互补
课堂总结:
反思本节课学到了什么?
你还有哪些疑问?
A
D
C
B
O
认真观察这幅图片,你能发现什么?
我们的幸福美好生活是亿万劳动者
撸起袖子加油干而努力奋斗出来的!
感谢他们!
如图1-2-3,已知∠AOC与∠BOD都是直角,∠BOC=60°.
(1)求∠AOB和∠DOC的度数;
(2)∠A OB与∠DOC有何大小关系;
(3)若不知道∠BOC的具体度数,其他条件不变,这种关系仍然成立吗?请说明理由.
作业与思考1.
(1)如图①,△ABC中,∠C=90°.则∠A是∠B的 。
(2)变式训练:在①的基础上,作∠CDA=900,如图②.
1.则∠A的余角有哪几个?为什么?
2.请找出图中相等的角,并说明理由.
作业与思考2.
C
A
B
C
A
B
D
图①
图②
2
1
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
