北师大版数学七年级下册:5.3 线段的轴对称性(2) 课件( 共17张PPT)
文档属性
| 名称 | 北师大版数学七年级下册:5.3 线段的轴对称性(2) 课件( 共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 189.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-03 14:48:10 | ||
图片预览




文档简介
5.3.2 简单的轴对称图形
——线段的轴对称性
1.什么是轴对称图形?
2.下列图形哪些是轴对称图形?
知识回顾
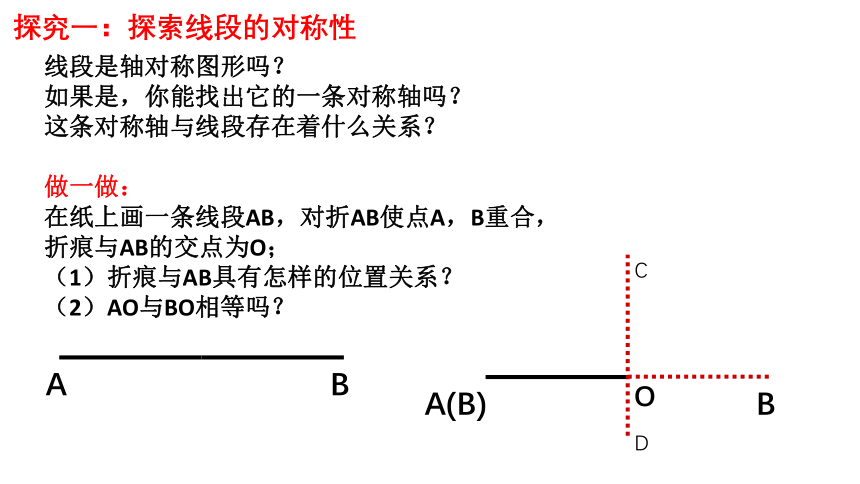
探究一:探索线段的对称性
A
B
A(B)
B
O
线段是轴对称图形吗?
如果是,你能找出它的一条对称轴吗?
这条对称轴与线段存在着什么关系?
做一做:
在纸上画一条线段AB,对折AB使点A,B重合,
折痕与AB的交点为O;
(1)折痕与AB具有怎样的位置关系?
(2)AO与BO相等吗?
C
D
(1)线段是轴对称图形,它的对称轴是直线CD,既垂直于AB又平分AB,称作AB的垂直平分线.
(2)线段垂直平分线的概念:
垂直于一条线段,并且平分这条线段的直线,叫做这条线段的垂直平分线(简称中垂线).
归纳:
(1)在折痕上任取一点C,沿CA将纸折叠
(2)把纸张展开,得到折痕CA和CB
(3)CA与CB相等吗?
(4)在折痕上移动点C的位置,结果会怎样?
能说明你的理由吗?
继续探究
A
B
P
O
C
A
B
P
O
C
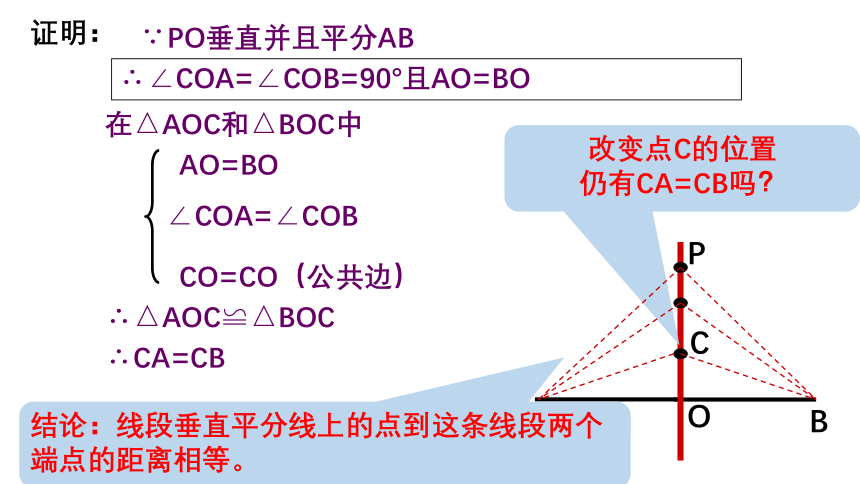
证明:
∵PO垂直并且平分AB
且AO=BO
∴∠COA=∠COB=90°且AO=BO
在△AOC和△BOC中
∴△AOC≌△BOC
AO=BO
∠COA=∠COB
CO=CO(公共边)
∴CA=CB
改变点C的位置
仍有CA=CB吗?
结论:线段垂直平分线上的点到这条线段两个端点的距离相等。
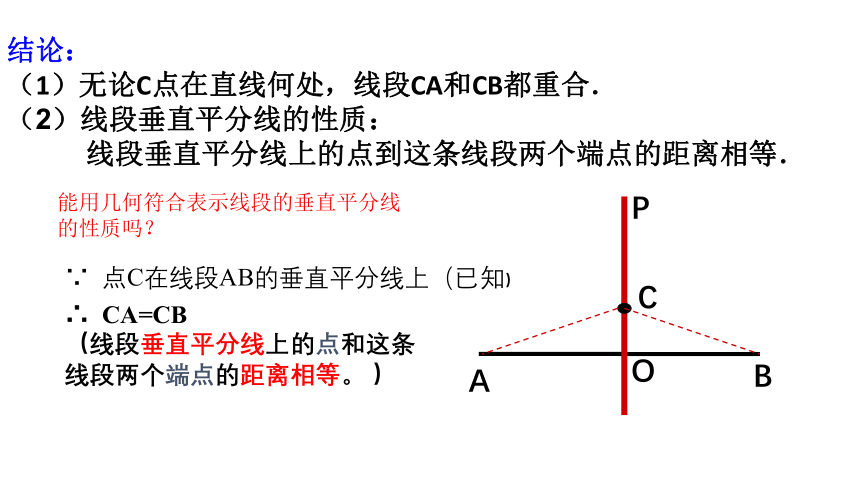
结论:
(1)无论C点在直线何处,线段CA和CB都重合.
(2)线段垂直平分线的性质:
线段垂直平分线上的点到这条线段两个端点的距离相等.
A
B
P
O
C
能用几何符合表示线段的垂直平分线的性质吗?
∵ 点C在线段AB的垂直平分线上(已知)
∴ CA=CB
(线段垂直平分线上的点和这条线段两个端点的距离相等。 )
跟踪训练
1、如图,直线l 是线段AB的垂直平分线,O、P分别是l上的两点,
则PA、PB、OA、OB的关系是( )
A
B
l
O
P
A、PA= OA ,PB=OB
B、PA= OA =PB=OB
C、PA=OB ,OA =PB
D、OA=OB ,A P=BP
D
2、如图,AB是△ABC的一条边,DE是AB的垂直平分线,垂足为E,并交BC于点D,已知AB=8cm,DB=6cm,那么EA=________, DA=____.
A
B
E
D
C
4cm
6cm
探究二:尺规作图
如图,已知线段AB,你能用尺规作出它的垂直平分线吗?
已知:线段AB
求作:线段AB的垂直平分线
A
B
C
D
如图,已知线段AB,画出它的垂直平分线.
做一做
做一做
如图,已知线段AB,画出它的垂直平分线.
作法:(1)分别以点A、点B为圆心,以大于
AB的长为半径画弧,两弧相交于点C和点D。
(2)经过点C、D作直线CD.
直线CD就是线段AB的垂直平分线。
拓展提高
A,B,C三点表示三个工厂,现要建一供水站,使它到这三个工厂的距离相等,请在图中标出供水站的位置P,请给予说明理由.
小结
⑴线段是轴对称图形吗?它的对称轴是什么?
⑵线段的垂直平分线的性质是什么?如何运用?
课后作业:
第一层次:习题5.4 第1、2题
第二层次:利用尺规作三角形重心
当堂达标
第1题
第2题
1.在△ABC中,BC=10,边BC的垂直平分线分别交AB,BC于点E,D,
BE=6,求△BCE的周长.
2.如图,AB是△ABC的一条边,DE是AB的垂直平分线,垂足为E,并交BC于点D,
已知AB=8cm,BD=6cm,那么EA=________, DA=____.
第3题
第4题
3. 如图,在△ABC中,AB=AC=16cm,AB的垂直平分线交AC于D,
如果BC=10cm,那么△BCD的周长是_______cm.
4.如图,已知点D在AB的垂直平分线上,如果AC=5cm,BC=4cm,那么△BDC的周长是 cm.
5.已知直线MN和DE分别是线段AB、BC的垂直平分线,它们交于P请问PA和PC相等吗?若相等请说明理由.
——线段的轴对称性
1.什么是轴对称图形?
2.下列图形哪些是轴对称图形?
知识回顾
探究一:探索线段的对称性
A
B
A(B)
B
O
线段是轴对称图形吗?
如果是,你能找出它的一条对称轴吗?
这条对称轴与线段存在着什么关系?
做一做:
在纸上画一条线段AB,对折AB使点A,B重合,
折痕与AB的交点为O;
(1)折痕与AB具有怎样的位置关系?
(2)AO与BO相等吗?
C
D
(1)线段是轴对称图形,它的对称轴是直线CD,既垂直于AB又平分AB,称作AB的垂直平分线.
(2)线段垂直平分线的概念:
垂直于一条线段,并且平分这条线段的直线,叫做这条线段的垂直平分线(简称中垂线).
归纳:
(1)在折痕上任取一点C,沿CA将纸折叠
(2)把纸张展开,得到折痕CA和CB
(3)CA与CB相等吗?
(4)在折痕上移动点C的位置,结果会怎样?
能说明你的理由吗?
继续探究
A
B
P
O
C
A
B
P
O
C
证明:
∵PO垂直并且平分AB
且AO=BO
∴∠COA=∠COB=90°且AO=BO
在△AOC和△BOC中
∴△AOC≌△BOC
AO=BO
∠COA=∠COB
CO=CO(公共边)
∴CA=CB
改变点C的位置
仍有CA=CB吗?
结论:线段垂直平分线上的点到这条线段两个端点的距离相等。
结论:
(1)无论C点在直线何处,线段CA和CB都重合.
(2)线段垂直平分线的性质:
线段垂直平分线上的点到这条线段两个端点的距离相等.
A
B
P
O
C
能用几何符合表示线段的垂直平分线的性质吗?
∵ 点C在线段AB的垂直平分线上(已知)
∴ CA=CB
(线段垂直平分线上的点和这条线段两个端点的距离相等。 )
跟踪训练
1、如图,直线l 是线段AB的垂直平分线,O、P分别是l上的两点,
则PA、PB、OA、OB的关系是( )
A
B
l
O
P
A、PA= OA ,PB=OB
B、PA= OA =PB=OB
C、PA=OB ,OA =PB
D、OA=OB ,A P=BP
D
2、如图,AB是△ABC的一条边,DE是AB的垂直平分线,垂足为E,并交BC于点D,已知AB=8cm,DB=6cm,那么EA=________, DA=____.
A
B
E
D
C
4cm
6cm
探究二:尺规作图
如图,已知线段AB,你能用尺规作出它的垂直平分线吗?
已知:线段AB
求作:线段AB的垂直平分线
A
B
C
D
如图,已知线段AB,画出它的垂直平分线.
做一做
做一做
如图,已知线段AB,画出它的垂直平分线.
作法:(1)分别以点A、点B为圆心,以大于
AB的长为半径画弧,两弧相交于点C和点D。
(2)经过点C、D作直线CD.
直线CD就是线段AB的垂直平分线。
拓展提高
A,B,C三点表示三个工厂,现要建一供水站,使它到这三个工厂的距离相等,请在图中标出供水站的位置P,请给予说明理由.
小结
⑴线段是轴对称图形吗?它的对称轴是什么?
⑵线段的垂直平分线的性质是什么?如何运用?
课后作业:
第一层次:习题5.4 第1、2题
第二层次:利用尺规作三角形重心
当堂达标
第1题
第2题
1.在△ABC中,BC=10,边BC的垂直平分线分别交AB,BC于点E,D,
BE=6,求△BCE的周长.
2.如图,AB是△ABC的一条边,DE是AB的垂直平分线,垂足为E,并交BC于点D,
已知AB=8cm,BD=6cm,那么EA=________, DA=____.
第3题
第4题
3. 如图,在△ABC中,AB=AC=16cm,AB的垂直平分线交AC于D,
如果BC=10cm,那么△BCD的周长是_______cm.
4.如图,已知点D在AB的垂直平分线上,如果AC=5cm,BC=4cm,那么△BDC的周长是 cm.
5.已知直线MN和DE分别是线段AB、BC的垂直平分线,它们交于P请问PA和PC相等吗?若相等请说明理由.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
