利用函数性质判定方程解的存在
图片预览




文档简介
(共15张PPT)
课件介绍
作者:高竹
单位:长安四中
使用方式:PPT
制作思路:
本课件是为高中数学必修一第四章《函数应用》中的第一节课制作的。由于本节内容对数形结合思想应用的非常多,所以利用课件会使得问题变得直观﹑简单;同时课件中丰富的色彩,简单的动画也会引起学生学习的兴趣。而且利用课件会节约很多画图﹑抄题的时间,这样就可以增大课堂容量,可给予学生充分的思考﹑练习﹑讨论的时间。
-1
0
1
2
3
x
y
1
-1
-2
-3
X=1
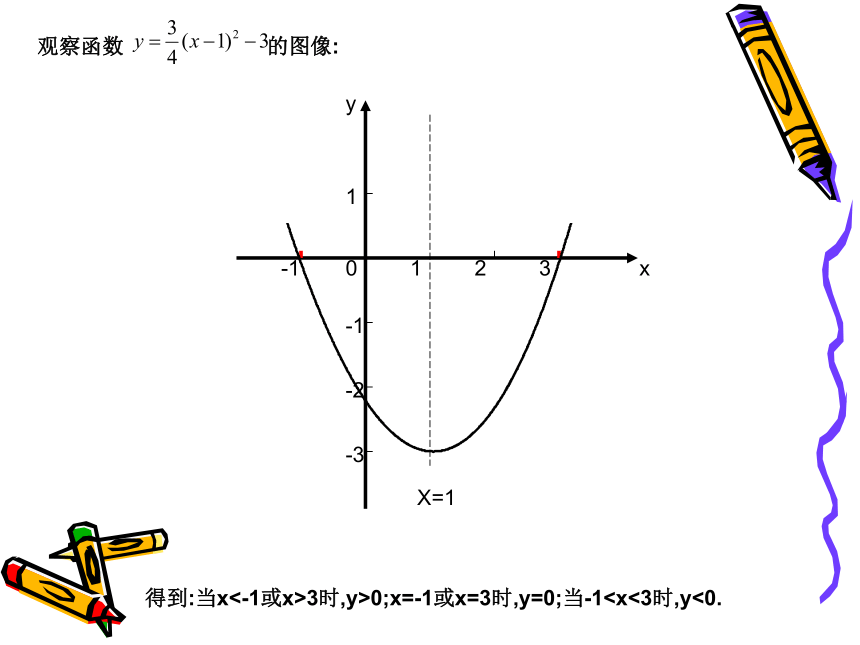
观察函数 的图像:
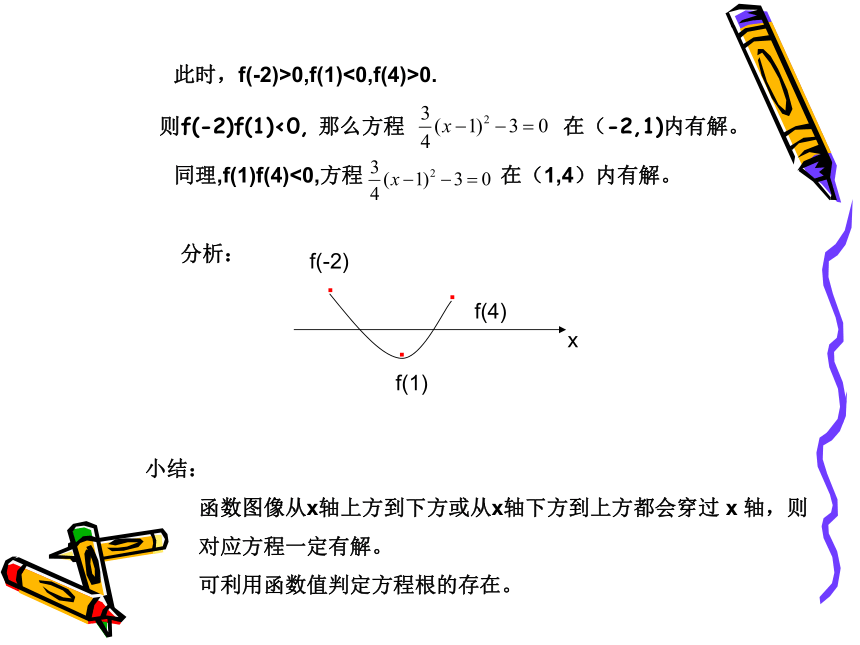
得到:当x<-1或x>3时,y>0;x=-1或x=3时,y=0;当-1此时,f(-2)>0,f(1)<0,f(4)>0.
同理,f(1)f(4)<0,方程 在(1,4)内有解。
分析:
·
·
·
x
f(-2)
f(4)
f(1)
小结:
函数图像从x轴上方到下方或从x轴下方到上方都会穿过 x 轴,则
对应方程一定有解。
可利用函数值判定方程根的存在。
则f(-2)f(1)<0, 那么方程 在(-2,1)内有解。
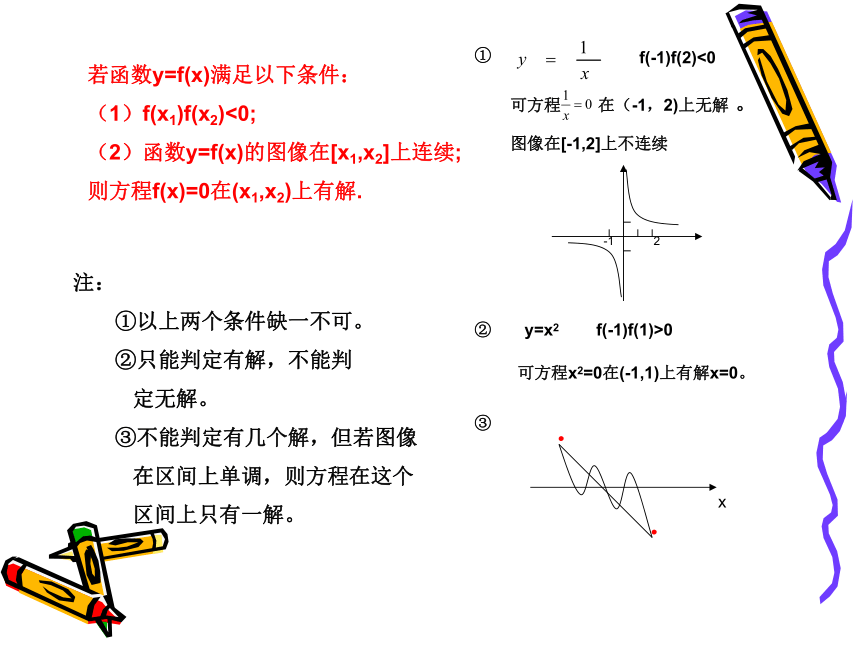
若函数y=f(x)满足以下条件:
(1)f(x1)f(x2)<0;
(2)函数y=f(x)的图像在[x1,x2]上连续;
则方程f(x)=0在(x1,x2)上有解.
注:
①以上两个条件缺一不可。
②只能判定有解,不能判
定无解。
③不能判定有几个解,但若图像
在区间上单调,则方程在这个
区间上只有一解。
f(-1)f(2)<0
可方程 在(-1,2)上无解 。
-1
2
图像在[-1,2]上不连续
①
②
y=x2
f(-1)f(1)>0
可方程x2=0在(-1,1)上有解x=0。
③
.
.
x
例1 判定方程x3+2x+1=0在[-2,3]上是否有解。
分析:
利用上述结论。
解:因为f(-2)=(-2)3+2×(-2)+1=-11<0
f(3)=33+2×3+1=34>0
则 f(-2)f(3)<0
又因为函数f(x)=x3+2x+1的图像在[-2,3]上连续,
所以,方程x3+2x+1=0在[-2,3]上有解。
小结:
①满足两个条件则可判定有解。
②一般地,若给定区间为函数定义域的子区间,则函
数图像在此区间上连续。
例2 判断方程 是否有解。
经试算f(0.1)=1- <0,f(100)=2- >0,
画出函数f(x)= 的图像如下:
y
x
0
1
Y=
从图可得:方程 有两个解,即为图中交点
的横坐标。
方法一:
方法二:
且函数f(x)= 的图像在[0.1,100]上连续,
所以方程 在(0.1,100)上有解。
题中方程可变形为
则可得到两个函数y= 及y=
可画出两个函数图象如下:
Y=
Y=
x
y
0
1
从图可得:方程 在(0,1)和(1,+∞)上各有一解。
①函数图象与x轴交点的横坐标叫做函数的零点,即
函数的零点为对应方程的解。
②利用函数图像判断方程的解更加直观。
③数形结合思想的应用。
④发散思维一题多解。
方法三:
小结:
课堂练习:
⒈判断方程x3-x=0在[-2,2]上是否有解。
分析:
思路一 f(-2)f(2)<0且f(x)=x3-x的图像在[-2,2] 上连续,
所以方程在此区间上有解。
思路二 数形结合
x
y
y=x3
y=x
1
1
-1
-1
0
从图可知方程有三个解
⒉判断方程x3+x=0 在(-∞,0)上是否有解。
分析:
思路一 利用值域判断
当x∈(-∞,0)时,f(x)<0 ,即图像在x轴下方,
函数在(-∞,0)上没有零点,则方程在(-∞,0)上
无解。
思路二 数形结合
x
y
1
1
-1
-1
0
y=x3
y=-x
从图可得方程无解
⒊利用函数增长的快慢判断方程x3=2x是否有解。
分析:
x
y
0
y=x3
y=2x
1
1
2
从图可看到方程有一解,
又因指数函数为爆炸函数,可知方程还有一解。
课堂小结:
①利用函数性质判定方程解的存在,例如,利用
函数值,图像等。
②要求熟练掌握利用函数值判定解存在的方法。
③理解数形结合思想在判定方程解存在中的应用。
布置作业:
判定下列方程在给定区间上是否有解:
⑴ x5+3x+1=0,x∈[-1,1];
⑵ ,x∈[-1,1];
⑶
,x∈[ - , ].
再见!
课件介绍
作者:高竹
单位:长安四中
使用方式:PPT
制作思路:
本课件是为高中数学必修一第四章《函数应用》中的第一节课制作的。由于本节内容对数形结合思想应用的非常多,所以利用课件会使得问题变得直观﹑简单;同时课件中丰富的色彩,简单的动画也会引起学生学习的兴趣。而且利用课件会节约很多画图﹑抄题的时间,这样就可以增大课堂容量,可给予学生充分的思考﹑练习﹑讨论的时间。
-1
0
1
2
3
x
y
1
-1
-2
-3
X=1
观察函数 的图像:
得到:当x<-1或x>3时,y>0;x=-1或x=3时,y=0;当-1
同理,f(1)f(4)<0,方程 在(1,4)内有解。
分析:
·
·
·
x
f(-2)
f(4)
f(1)
小结:
函数图像从x轴上方到下方或从x轴下方到上方都会穿过 x 轴,则
对应方程一定有解。
可利用函数值判定方程根的存在。
则f(-2)f(1)<0, 那么方程 在(-2,1)内有解。
若函数y=f(x)满足以下条件:
(1)f(x1)f(x2)<0;
(2)函数y=f(x)的图像在[x1,x2]上连续;
则方程f(x)=0在(x1,x2)上有解.
注:
①以上两个条件缺一不可。
②只能判定有解,不能判
定无解。
③不能判定有几个解,但若图像
在区间上单调,则方程在这个
区间上只有一解。
f(-1)f(2)<0
可方程 在(-1,2)上无解 。
-1
2
图像在[-1,2]上不连续
①
②
y=x2
f(-1)f(1)>0
可方程x2=0在(-1,1)上有解x=0。
③
.
.
x
例1 判定方程x3+2x+1=0在[-2,3]上是否有解。
分析:
利用上述结论。
解:因为f(-2)=(-2)3+2×(-2)+1=-11<0
f(3)=33+2×3+1=34>0
则 f(-2)f(3)<0
又因为函数f(x)=x3+2x+1的图像在[-2,3]上连续,
所以,方程x3+2x+1=0在[-2,3]上有解。
小结:
①满足两个条件则可判定有解。
②一般地,若给定区间为函数定义域的子区间,则函
数图像在此区间上连续。
例2 判断方程 是否有解。
经试算f(0.1)=1- <0,f(100)=2- >0,
画出函数f(x)= 的图像如下:
y
x
0
1
Y=
从图可得:方程 有两个解,即为图中交点
的横坐标。
方法一:
方法二:
且函数f(x)= 的图像在[0.1,100]上连续,
所以方程 在(0.1,100)上有解。
题中方程可变形为
则可得到两个函数y= 及y=
可画出两个函数图象如下:
Y=
Y=
x
y
0
1
从图可得:方程 在(0,1)和(1,+∞)上各有一解。
①函数图象与x轴交点的横坐标叫做函数的零点,即
函数的零点为对应方程的解。
②利用函数图像判断方程的解更加直观。
③数形结合思想的应用。
④发散思维一题多解。
方法三:
小结:
课堂练习:
⒈判断方程x3-x=0在[-2,2]上是否有解。
分析:
思路一 f(-2)f(2)<0且f(x)=x3-x的图像在[-2,2] 上连续,
所以方程在此区间上有解。
思路二 数形结合
x
y
y=x3
y=x
1
1
-1
-1
0
从图可知方程有三个解
⒉判断方程x3+x=0 在(-∞,0)上是否有解。
分析:
思路一 利用值域判断
当x∈(-∞,0)时,f(x)<0 ,即图像在x轴下方,
函数在(-∞,0)上没有零点,则方程在(-∞,0)上
无解。
思路二 数形结合
x
y
1
1
-1
-1
0
y=x3
y=-x
从图可得方程无解
⒊利用函数增长的快慢判断方程x3=2x是否有解。
分析:
x
y
0
y=x3
y=2x
1
1
2
从图可看到方程有一解,
又因指数函数为爆炸函数,可知方程还有一解。
课堂小结:
①利用函数性质判定方程解的存在,例如,利用
函数值,图像等。
②要求熟练掌握利用函数值判定解存在的方法。
③理解数形结合思想在判定方程解存在中的应用。
布置作业:
判定下列方程在给定区间上是否有解:
⑴ x5+3x+1=0,x∈[-1,1];
⑵ ,x∈[-1,1];
⑶
,x∈[ - , ].
再见!
