沪教版(上海)初中数学九年级第一学期 26.3 二次函数专题复习 教案
文档属性
| 名称 | 沪教版(上海)初中数学九年级第一学期 26.3 二次函数专题复习 教案 |
|
|
| 格式 | zip | ||
| 文件大小 | 65.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-04 06:19:03 | ||
图片预览

文档简介
二次函数专题复习
一、教学目标
1.
巩固二次函数的图像及其基本性质;
2.
能利用二次函数性质、相似三角形性质和三角比性质解决综合性问题;
3.
通过小组合作探究过程体会数形结合、分类讨论、方程思想等数学思想方法在解题中的运用。
二、教学重点和难点
教学重点:运用相关知识解决二次函数的综合性问题;
教学难点:动点变化过程中,利用方程和分类讨论思想解决问题。
三、教学过程
(一)你来设计
你来做
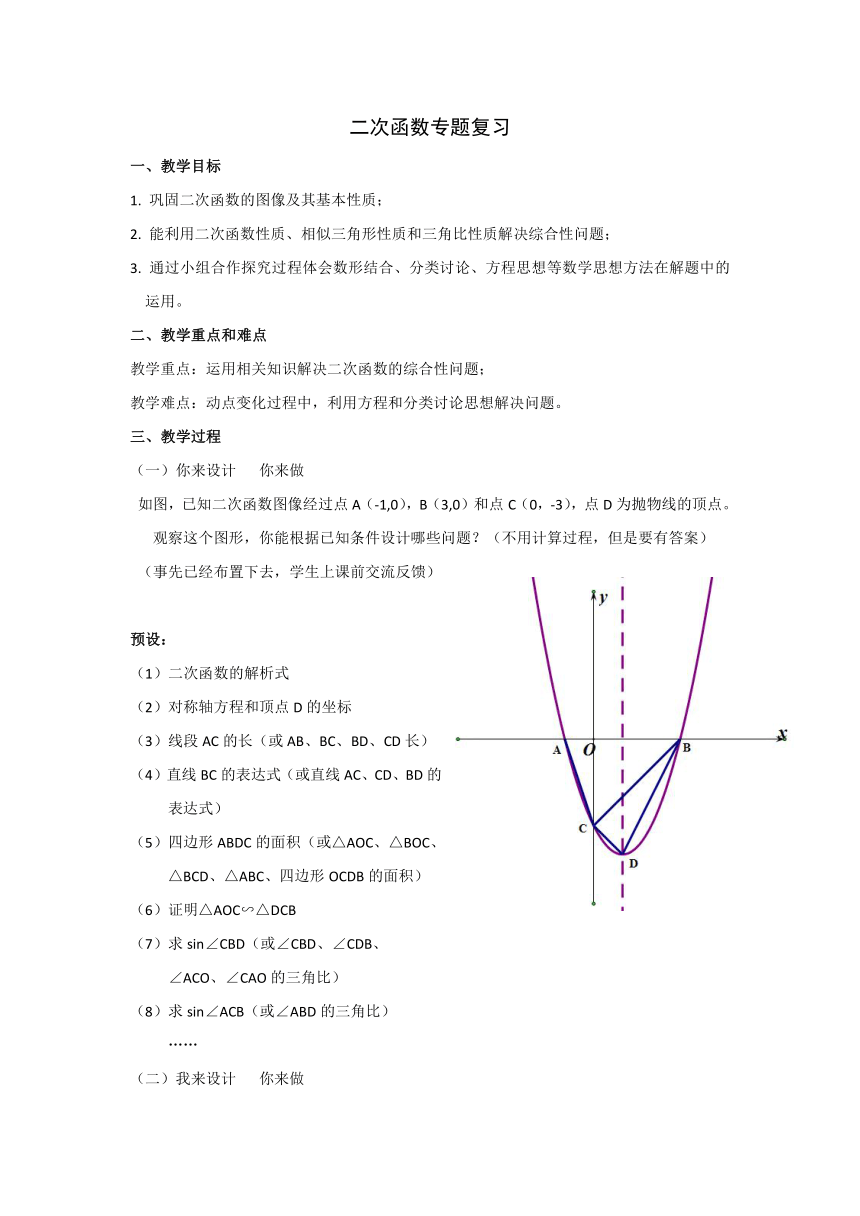
如图,已知二次函数图像经过点A(-1,0),B(3,0)和点C(0,-3),点D为抛物线的顶点。
观察这个图形,你能根据已知条件设计哪些问题?(不用计算过程,但是要有答案)
(事先已经布置下去,学生上课前交流反馈)
预设:
(1)二次函数的解析式
(2)对称轴方程和顶点D的坐标
(3)线段AC的长(或AB、BC、BD、CD长)
(4)直线BC的表达式(或直线AC、CD、BD的
表达式)
(5)四边形ABDC的面积(或△AOC、△BOC、
△BCD、△ABC、四边形OCDB的面积)
(6)证明△AOC∽△DCB
(7)求sin∠CBD(或∠CBD、∠CDB、
∠ACO、∠CAO的三角比)
(8)求sin∠ACB(或∠ABD的三角比)
……
(二)我来设计
你来做
例1:如题1,
如果点E是抛物线上一点且满足∠EAB=∠CBD,求点E坐标;
例2:如题1:
点E是抛物线对称轴上一点,当以E、C、D为顶点的三角形与△ABC相似时,求点E坐标.
设计以上两题目的:
1、考虑问题的严密性---分类讨论
2、分析问题的典型性---例1中角的问题转化为边的问题;例2中动点相似里定角的确定
3、解决问题的合理性---线段与坐标的匹配
四、课内小结
今天我的收获是
我还需要加强的是
五、布置作业
(1)
同题1,若以点C为圆心,CB为半径的圆与直线BD的另一个交点为点E,求点E的坐标。
(用两种不同的方法求解)
(2)你来设计
同学做
以小组为单位,在前期设计的基础上每个小组再设计一个令本组同学满意的题,各小组进行交换解答
一、教学目标
1.
巩固二次函数的图像及其基本性质;
2.
能利用二次函数性质、相似三角形性质和三角比性质解决综合性问题;
3.
通过小组合作探究过程体会数形结合、分类讨论、方程思想等数学思想方法在解题中的运用。
二、教学重点和难点
教学重点:运用相关知识解决二次函数的综合性问题;
教学难点:动点变化过程中,利用方程和分类讨论思想解决问题。
三、教学过程
(一)你来设计
你来做
如图,已知二次函数图像经过点A(-1,0),B(3,0)和点C(0,-3),点D为抛物线的顶点。
观察这个图形,你能根据已知条件设计哪些问题?(不用计算过程,但是要有答案)
(事先已经布置下去,学生上课前交流反馈)
预设:
(1)二次函数的解析式
(2)对称轴方程和顶点D的坐标
(3)线段AC的长(或AB、BC、BD、CD长)
(4)直线BC的表达式(或直线AC、CD、BD的
表达式)
(5)四边形ABDC的面积(或△AOC、△BOC、
△BCD、△ABC、四边形OCDB的面积)
(6)证明△AOC∽△DCB
(7)求sin∠CBD(或∠CBD、∠CDB、
∠ACO、∠CAO的三角比)
(8)求sin∠ACB(或∠ABD的三角比)
……
(二)我来设计
你来做
例1:如题1,
如果点E是抛物线上一点且满足∠EAB=∠CBD,求点E坐标;
例2:如题1:
点E是抛物线对称轴上一点,当以E、C、D为顶点的三角形与△ABC相似时,求点E坐标.
设计以上两题目的:
1、考虑问题的严密性---分类讨论
2、分析问题的典型性---例1中角的问题转化为边的问题;例2中动点相似里定角的确定
3、解决问题的合理性---线段与坐标的匹配
四、课内小结
今天我的收获是
我还需要加强的是
五、布置作业
(1)
同题1,若以点C为圆心,CB为半径的圆与直线BD的另一个交点为点E,求点E的坐标。
(用两种不同的方法求解)
(2)你来设计
同学做
以小组为单位,在前期设计的基础上每个小组再设计一个令本组同学满意的题,各小组进行交换解答
