鲁教五四版八年级数学上学期 5.4 多边形的内角和与外角和 同步练习(word解析版)
文档属性
| 名称 | 鲁教五四版八年级数学上学期 5.4 多边形的内角和与外角和 同步练习(word解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 126.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-04 09:47:30 | ||
图片预览


文档简介
5.4
多边形的内角和与外角和
一.选择题
1.已知,正n边形的每一个内角是144°,则n的值是( )
A.6
B.8
C.10
D.12
2.一个多边形少算一个内角,其余内角之和是1500°,则这个多边形的边数是( )
A.8
B.9
C.10
D.11
3.八年级一班的同学体育课上玩游戏,让小聪同学从A出发前进10米后左转30°,再前进10米后左转30°,按照这样方法一直走下去,当他回到A时,共走了( )
A.60米
B.100米
C.120米
D.150米
4.过六边形的一个顶点的对角线共有( )条.
A.1
B.2
C.3
D.4
5.若n边形的内角和是它外角和的4倍,则n等于( )
A.8
B.9
C.10
D.11
6.某多边形内角和与外角和共1080°,则这个多边形的边数为( )
A.6
B.7
C.8
D.9
7.如图,在五边形ABCDE中,∠A+∠B+∠E=320°,DP,CP分别平分∠EDC,∠BCD,则∠P的度数是( )
A.70°
B.65°
C.60°
D.55°
8.下列说法中正确的是( )
A.三角形的外角和等于它的内角和
B.三角形的一个外角大于任何一个与它不相邻的内角
C.三角形的外角大于任何一个内角
D.三角形的一个外角和内角互补
二.填空题
9.已知一个n边形的内角和是900°,则n=
.
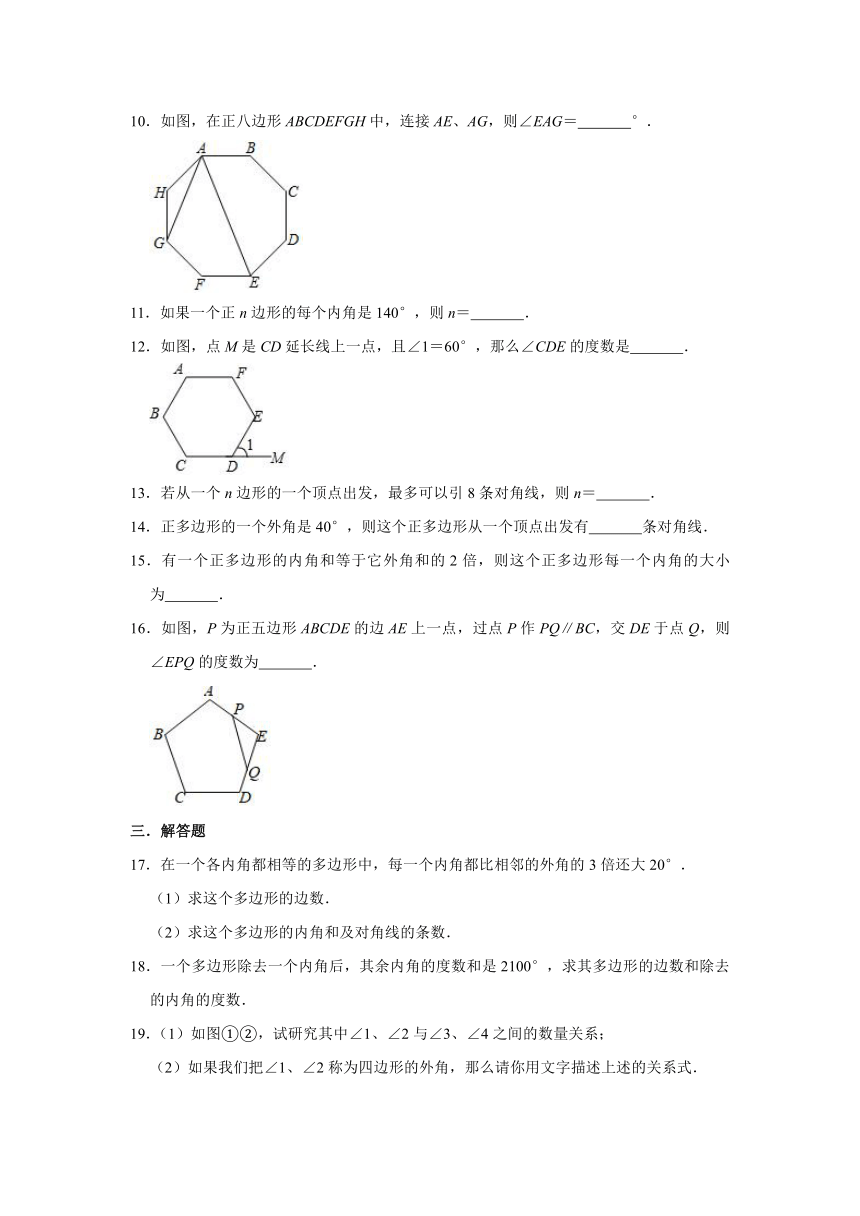
10.如图,在正八边形ABCDEFGH中,连接AE、AG,则∠EAG=
°.
11.如果一个正n边形的每个内角是140°,则n=
.
12.如图,点M是CD延长线上一点,且∠1=60°,那么∠CDE的度数是
.
13.若从一个n边形的一个顶点出发,最多可以引8条对角线,则n=
.
14.正多边形的一个外角是40°,则这个正多边形从一个顶点出发有
条对角线.
15.有一个正多边形的内角和等于它外角和的2倍,则这个正多边形每一个内角的大小为
.
16.如图,P为正五边形ABCDE的边AE上一点,过点P作PQ∥BC,交DE于点Q,则∠EPQ的度数为
.
三.解答题
17.在一个各内角都相等的多边形中,每一个内角都比相邻的外角的3倍还大20°.
(1)求这个多边形的边数.
(2)求这个多边形的内角和及对角线的条数.
18.一个多边形除去一个内角后,其余内角的度数和是2100°,求其多边形的边数和除去的内角的度数.
19.(1)如图①②,试研究其中∠1、∠2与∠3、∠4之间的数量关系;
(2)如果我们把∠1、∠2称为四边形的外角,那么请你用文字描述上述的关系式.
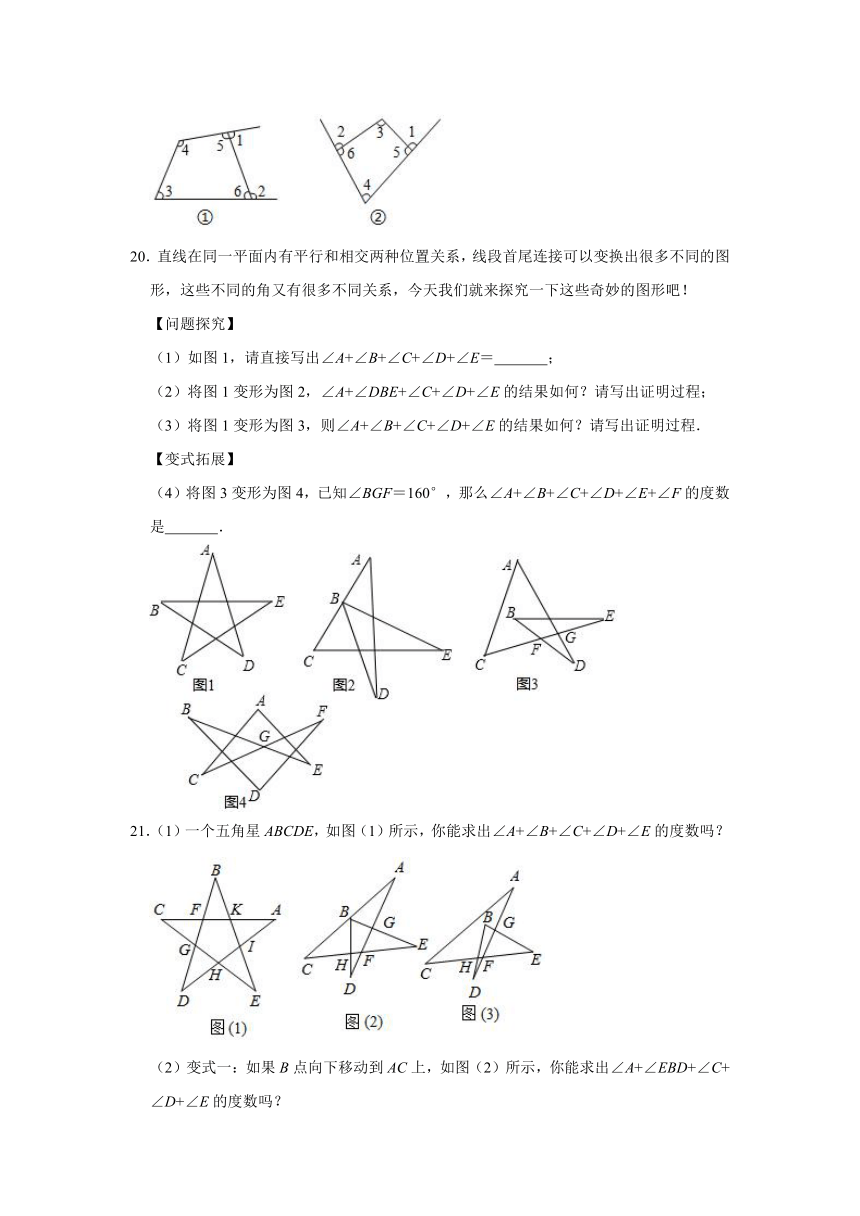
20.直线在同一平面内有平行和相交两种位置关系,线段首尾连接可以变换出很多不同的图形,这些不同的角又有很多不同关系,今天我们就来探究一下这些奇妙的图形吧!
【问题探究】
(1)如图1,请直接写出∠A+∠B+∠C+∠D+∠E=
;
(2)将图1变形为图2,∠A+∠DBE+∠C+∠D+∠E的结果如何?请写出证明过程;
(3)将图1变形为图3,则∠A+∠B+∠C+∠D+∠E的结果如何?请写出证明过程.
【变式拓展】
(4)将图3变形为图4,已知∠BGF=160°,那么∠A+∠B+∠C+∠D+∠E+∠F的度数是
.
21.(1)一个五角星ABCDE,如图(1)所示,你能求出∠A+∠B+∠C+∠D+∠E的度数吗?
(2)变式一:如果B点向下移动到AC上,如图(2)所示,你能求出∠A+∠EBD+∠C+∠D+∠E的度数吗?
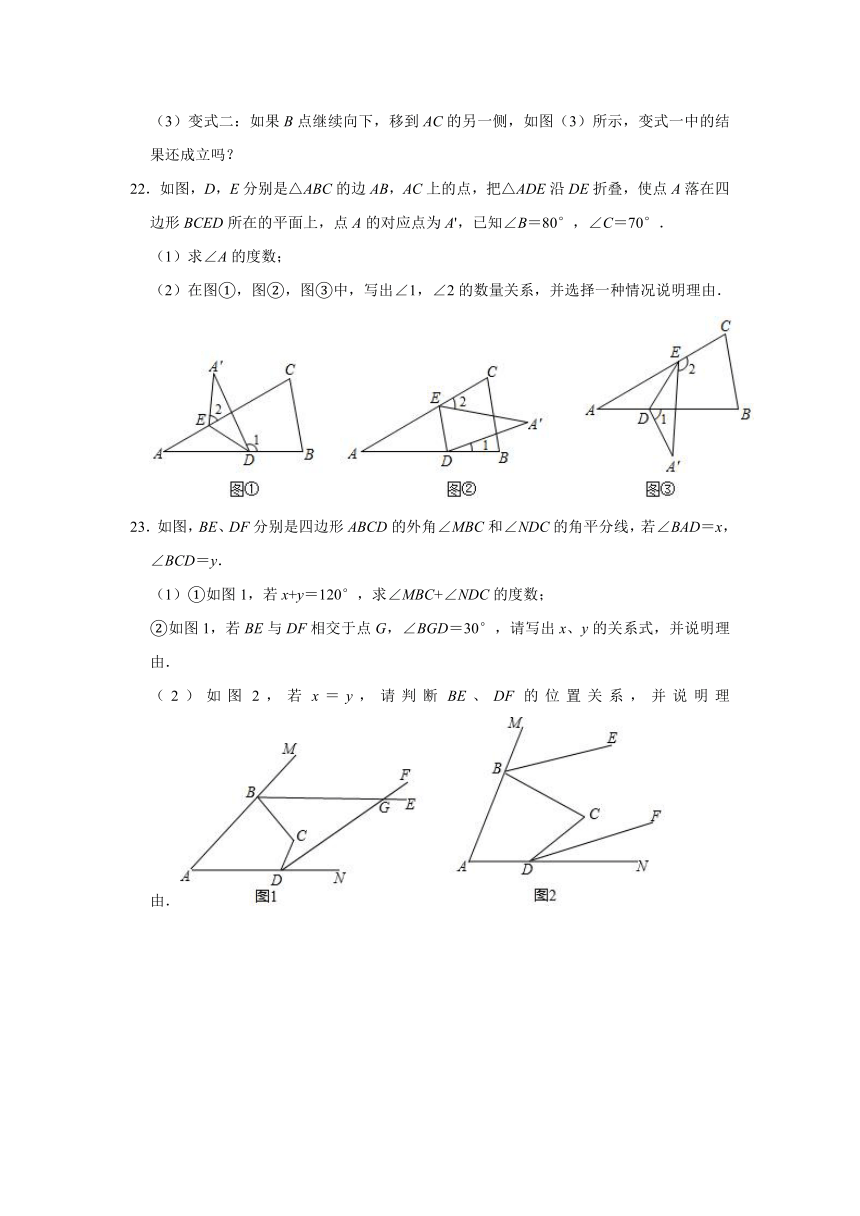
(3)变式二:如果B点继续向下,移到AC的另一侧,如图(3)所示,变式一中的结果还成立吗?
22.如图,D,E分别是△ABC的边AB,AC上的点,把△ADE沿DE折叠,使点A落在四边形BCED所在的平面上,点A的对应点为A',已知∠B=80°,∠C=70°.
(1)求∠A的度数;
(2)在图①,图②,图③中,写出∠1,∠2的数量关系,并选择一种情况说明理由.
23.如图,BE、DF分别是四边形ABCD的外角∠MBC和∠NDC的角平分线,若∠BAD=x,∠BCD=y.
(1)①如图1,若x+y=120°,求∠MBC+∠NDC的度数;
②如图1,若BE与DF相交于点G,∠BGD=30°,请写出x、y的关系式,并说明理由.
(2)如图2,若x=y,请判断BE、DF的位置关系,并说明理由.
参考答案
一.选择题
1.解:∵正n边形的每一个内角都等于144°,
∴每一个外角都是180﹣144=36(度),
∴n=360÷36=10.
故选:C.
2.解:1500÷180=8,
则正多边形的边数是8+1+2=11.
故选:D.
3.解:∵多边形的外角和为360°,
∴=12,
即12×10米=120米,
故选:C.
4.解:六边形从一个顶点可引出对角线:6﹣3=3(条),
故选:C.
5.解:多边形的外角和是360°,根据题意得:
180°?(n﹣2)=360°×4,
解得n=10.
故选:C.
6.解:∵多边形内角和与外角和共1080°,
∴多边形内角和=1080°﹣360°=720°,
设多边形的边数是n,
∴(n﹣2)×180°=720°,
解得n=6.
故选:A.
7.解:∵五边形的内角和等于540°,∠A+∠B+∠E=320°,
∴∠BCD+∠CDE=540°﹣320°=220°,
∵∠BCD、∠CDE的平分线在五边形内相交于点P,
∴∠PDC+∠PCD=(∠BCD+∠CDE)=110°,
∴∠CPD=180°﹣110°=70°.
故选:A.
8.解:A、三角形的外角等于和它不相邻的两个内角的和,故此选项错误;
B、三角形的一个外角大于任何一个与它不相邻的内角,故此选项正确;
C、三角形的外角大于不相邻的内角,故此选项错误;
D、三角形的一个外角和与它相邻的内角互补,故此选项错误.
故选:B.
二.填空题
9.解:这个多边形的边数是n,
则:(n﹣2)?180°=900°,
解得n=7.
故答案为:7.
10.解:连接AC、GE、EC,如图所示:
在正八边形ABCDEFGH中,
∵AB=AH,∠H=∠B=∠HAB=135°,HG=BC,
∴△AHG≌△ABC(SAS),
∴AG=AC,∠HAG=∠BAC=22.5°,
∴∠GAC=90°,
同理,EG=CE=AG,
∴四边形ACEG为正方形,
∴∠EAG=45°,
故答案为:45.
11.解:∵正n边形的每个内角都是140°,
∴正n边形的每个外角的度数=180°﹣140°=40°,
∴n==9.
故答案为:9.
12.解:∠CDE=180°﹣∠1=180°﹣60°=120°,
故答案为120°.
13.解:设多边形有n条边,
则n﹣3=8,解得n=11.
故答案为:11.
14.解:360°÷40°=9,
9﹣3=6.
故这个正多边形从一个顶点出发可以作的对角线条数是6.
故答案为:6.
15.解:∵一个正多边形的内角和等于它外角和的2倍,任意多边形的外角和都是360°,
∴这个多边形的内角和是360°×2=720°,
设这个正多边形的边数为n,
则(n﹣2)×180°=720°,
解得n=6,
故这个正多边形每一个内角的大小为720°÷6=120°,
故答案为:120°.
16.解:连接AD,
∵五边形ABCDE是正五边形,
∴∠B=∠BAE=∠E∠EDC=∠C=108°,AE=DE,
∴∠AED=∠EDA=36°,
∴∠BAD=72°,
∵∠BAD+∠ABC=180°,
∴BC∥AD,
∵PQ∥BC,
∴AD∥PQ,
∴∠EPQ=∠EAD=36°,
故答案为:36°.
三.解答题
17.解:(1)设多边形的一个外角为α°,则与其相邻的内角为(3α+20)°,
由题意,得(3α+20)+α=180.
解得α=40,
即多边形的每个外角为40°,
∵多边形的外角和为360°,
∴多边形的边数为360°÷40°=9;
答:这个多边形的边数为9;
(2)这个多边形的内角和为(9﹣2)×180°=1260°,
对角线一共有×(9﹣3)×9=27(条),
答:内角和1260°,对角线27条.
18.解:2100÷180=11,
则正多边形的边数是11+1+2=14边形.
除去的内角的度数为:(14﹣2)×180°﹣2100°=60°.
19.解:(1)∵∠3、∠4、∠5、∠6是四边形的四个内角,
∴∠3+∠4+∠5+∠6=360°,
∴∠3+∠4=360°﹣(∠5+∠6),
∵∠1+∠5=180°,∠2+∠6=180°,
∴∠1+∠2=360°﹣(∠5+∠6),
∴∠1+∠2=∠3+∠4;
(2)四边形的任意两个外角的和等于与它们不相邻的两个内角的和.
20.(1)解:如图1,∵∠2=∠C+∠E,∠1=∠A+∠2,
∴∠A+∠B+∠C+∠D+∠E=∠1+∠B+∠D=180°,
故答案为:180°;
(2)证明:∵∠ABE=∠C+∠E,∠DBC=∠A+∠D,
∠ABE+∠DBE+∠DBC=180°,
∴∠A+∠DBE+∠C+∠D+∠E=180°
∴将图①变形成图②∠A+∠DBE+∠C+∠D+∠E仍然为180°;
(3)证明:∵在△FGD中,∠DFG+∠FGD+∠D=180°,
∠DFG=∠B+∠E,∠FGD=∠A+∠C,
∴∠A+∠B+∠C+∠D+∠E=180°,
∴将图①变形成图③,则∠A+∠B+∠C+∠D+∠E还为180°;
(4)解:∵∠BGF=∠B+∠2=160°,∠2=∠D+∠F,
∴∠B+∠D+∠F=160°,
∵∠BGF=∠1+∠E=160°,∠1=∠A+∠C,
∴∠A+∠C+∠E=160°,
∴∠A+∠B+∠C+∠D+∠E+∠F=320°,
故答案为:320°.
21.解:(1)如图1,∵∠BFG=∠C+∠E,∠BGF=∠A+∠D,
又∵∠B+∠BFG+∠BGF=180°,
∴∠A+∠B+∠C+∠D+∠E=180°;
(2)如图2,∵∠A+∠C=∠1,∠DBE+∠E=∠2,
又∵∠1+∠2+∠D=180°,
∴∠A+∠C+∠DBE+∠E+∠D=180°;
(3)如图3,∵∠B+∠E=∠2,∠A+∠C=∠1,
由三角形内角和定理可知∠1+∠2+∠E=180°,
即∠B+∠D+∠A+∠C+∠E=180°,故结论都成立.
22.解:(1)∵∠B=80°,∠C=70°,
∴∠A=180°﹣(∠B+∠C)=180°﹣(80°+70°)=30°;
(2)如图①,∵把△ADE沿DE折叠,使点A落在四边形BCED所在的平面上,点A的对应点为A',
∴∠A′=∠A=30°,
∴∠3=180°﹣∠A′﹣∠2=150°﹣∠2,
∵∠1+∠3+∠B+∠C=360°,
∴∠1+150°﹣∠2+80°+70°=360°,
∴∠1﹣∠2=60°;
如图②,∵把△ADE沿DE折叠,使点A落在四边形BCED所在的平面上,点A的对应点为A',
∴∠A′=∠A=30°,
∴∠AEA′+∠ADA′=360°﹣∠A﹣∠A′=300°,
∴∠1+∠2=360°﹣∠AEA′﹣∠ADA′=60°;
如图③,方法同①,∠2﹣∠1=60°.
23.解:(1)①∵∠ABC+∠ADC=360°﹣(x+y)=240°,
∴∠MBC+∠NDC=180°﹣∠ABC+180°﹣∠ADC=x+y=120°;
②y﹣x=60°.
理由:如图1,连接BD,
由①有,∠MBC+∠NDC=x+y,
∵BE、DF分别平分四边形的外角∠MBC和∠NDC,
∴∠CBG=∠MBC,∠CDG=∠NDC,
∴∠CBG+∠CDG=∠MBC+∠NDC=(∠MBC+∠NDC)=(x+y),
在△BCD中,∠BDC+∠CBD=180°﹣∠BCD=180°﹣y,
在△BDG中,∠GBD+∠GDB+∠BGD=180°,
∴∠CBG+∠CBD+∠CDG+∠BDC+∠BGD=180°,
∴(∠CBG+∠CDG)+(∠BDC+∠CBD)+∠BGD=180°,
∴(x+y)+180°﹣y+30°=180°,
∴y﹣x=60°;
(2)BE∥DF.
理由:如图2,延长BC交DF于H,
由(1)有,∠MBC+∠NDC=x+y,
∵BE、DF分别平分四边形的外角∠MBC和∠NDC,
∴∠CBE=∠MBC,∠CDH=∠NDC,
∴∠CBE+∠CDH=∠MBC+∠NDC=(∠MBC+∠NDC)=(α+β),
∵∠BCD=∠CDH+∠DHB,
∴∠CDH=∠BCD﹣∠DHB=y﹣∠DHB,
∴∠CBE+y﹣∠DHB=(x+y),
∵x=y,
∴∠CBE+y﹣∠DHB=(y+y)=y,
∴∠CBE=∠DHB,
∴BE∥DF.
多边形的内角和与外角和
一.选择题
1.已知,正n边形的每一个内角是144°,则n的值是( )
A.6
B.8
C.10
D.12
2.一个多边形少算一个内角,其余内角之和是1500°,则这个多边形的边数是( )
A.8
B.9
C.10
D.11
3.八年级一班的同学体育课上玩游戏,让小聪同学从A出发前进10米后左转30°,再前进10米后左转30°,按照这样方法一直走下去,当他回到A时,共走了( )
A.60米
B.100米
C.120米
D.150米
4.过六边形的一个顶点的对角线共有( )条.
A.1
B.2
C.3
D.4
5.若n边形的内角和是它外角和的4倍,则n等于( )
A.8
B.9
C.10
D.11
6.某多边形内角和与外角和共1080°,则这个多边形的边数为( )
A.6
B.7
C.8
D.9
7.如图,在五边形ABCDE中,∠A+∠B+∠E=320°,DP,CP分别平分∠EDC,∠BCD,则∠P的度数是( )
A.70°
B.65°
C.60°
D.55°
8.下列说法中正确的是( )
A.三角形的外角和等于它的内角和
B.三角形的一个外角大于任何一个与它不相邻的内角
C.三角形的外角大于任何一个内角
D.三角形的一个外角和内角互补
二.填空题
9.已知一个n边形的内角和是900°,则n=
.
10.如图,在正八边形ABCDEFGH中,连接AE、AG,则∠EAG=
°.
11.如果一个正n边形的每个内角是140°,则n=
.
12.如图,点M是CD延长线上一点,且∠1=60°,那么∠CDE的度数是
.
13.若从一个n边形的一个顶点出发,最多可以引8条对角线,则n=
.
14.正多边形的一个外角是40°,则这个正多边形从一个顶点出发有
条对角线.
15.有一个正多边形的内角和等于它外角和的2倍,则这个正多边形每一个内角的大小为
.
16.如图,P为正五边形ABCDE的边AE上一点,过点P作PQ∥BC,交DE于点Q,则∠EPQ的度数为
.
三.解答题
17.在一个各内角都相等的多边形中,每一个内角都比相邻的外角的3倍还大20°.
(1)求这个多边形的边数.
(2)求这个多边形的内角和及对角线的条数.
18.一个多边形除去一个内角后,其余内角的度数和是2100°,求其多边形的边数和除去的内角的度数.
19.(1)如图①②,试研究其中∠1、∠2与∠3、∠4之间的数量关系;
(2)如果我们把∠1、∠2称为四边形的外角,那么请你用文字描述上述的关系式.
20.直线在同一平面内有平行和相交两种位置关系,线段首尾连接可以变换出很多不同的图形,这些不同的角又有很多不同关系,今天我们就来探究一下这些奇妙的图形吧!
【问题探究】
(1)如图1,请直接写出∠A+∠B+∠C+∠D+∠E=
;
(2)将图1变形为图2,∠A+∠DBE+∠C+∠D+∠E的结果如何?请写出证明过程;
(3)将图1变形为图3,则∠A+∠B+∠C+∠D+∠E的结果如何?请写出证明过程.
【变式拓展】
(4)将图3变形为图4,已知∠BGF=160°,那么∠A+∠B+∠C+∠D+∠E+∠F的度数是
.
21.(1)一个五角星ABCDE,如图(1)所示,你能求出∠A+∠B+∠C+∠D+∠E的度数吗?
(2)变式一:如果B点向下移动到AC上,如图(2)所示,你能求出∠A+∠EBD+∠C+∠D+∠E的度数吗?
(3)变式二:如果B点继续向下,移到AC的另一侧,如图(3)所示,变式一中的结果还成立吗?
22.如图,D,E分别是△ABC的边AB,AC上的点,把△ADE沿DE折叠,使点A落在四边形BCED所在的平面上,点A的对应点为A',已知∠B=80°,∠C=70°.
(1)求∠A的度数;
(2)在图①,图②,图③中,写出∠1,∠2的数量关系,并选择一种情况说明理由.
23.如图,BE、DF分别是四边形ABCD的外角∠MBC和∠NDC的角平分线,若∠BAD=x,∠BCD=y.
(1)①如图1,若x+y=120°,求∠MBC+∠NDC的度数;
②如图1,若BE与DF相交于点G,∠BGD=30°,请写出x、y的关系式,并说明理由.
(2)如图2,若x=y,请判断BE、DF的位置关系,并说明理由.
参考答案
一.选择题
1.解:∵正n边形的每一个内角都等于144°,
∴每一个外角都是180﹣144=36(度),
∴n=360÷36=10.
故选:C.
2.解:1500÷180=8,
则正多边形的边数是8+1+2=11.
故选:D.
3.解:∵多边形的外角和为360°,
∴=12,
即12×10米=120米,
故选:C.
4.解:六边形从一个顶点可引出对角线:6﹣3=3(条),
故选:C.
5.解:多边形的外角和是360°,根据题意得:
180°?(n﹣2)=360°×4,
解得n=10.
故选:C.
6.解:∵多边形内角和与外角和共1080°,
∴多边形内角和=1080°﹣360°=720°,
设多边形的边数是n,
∴(n﹣2)×180°=720°,
解得n=6.
故选:A.
7.解:∵五边形的内角和等于540°,∠A+∠B+∠E=320°,
∴∠BCD+∠CDE=540°﹣320°=220°,
∵∠BCD、∠CDE的平分线在五边形内相交于点P,
∴∠PDC+∠PCD=(∠BCD+∠CDE)=110°,
∴∠CPD=180°﹣110°=70°.
故选:A.
8.解:A、三角形的外角等于和它不相邻的两个内角的和,故此选项错误;
B、三角形的一个外角大于任何一个与它不相邻的内角,故此选项正确;
C、三角形的外角大于不相邻的内角,故此选项错误;
D、三角形的一个外角和与它相邻的内角互补,故此选项错误.
故选:B.
二.填空题
9.解:这个多边形的边数是n,
则:(n﹣2)?180°=900°,
解得n=7.
故答案为:7.
10.解:连接AC、GE、EC,如图所示:
在正八边形ABCDEFGH中,
∵AB=AH,∠H=∠B=∠HAB=135°,HG=BC,
∴△AHG≌△ABC(SAS),
∴AG=AC,∠HAG=∠BAC=22.5°,
∴∠GAC=90°,
同理,EG=CE=AG,
∴四边形ACEG为正方形,
∴∠EAG=45°,
故答案为:45.
11.解:∵正n边形的每个内角都是140°,
∴正n边形的每个外角的度数=180°﹣140°=40°,
∴n==9.
故答案为:9.
12.解:∠CDE=180°﹣∠1=180°﹣60°=120°,
故答案为120°.
13.解:设多边形有n条边,
则n﹣3=8,解得n=11.
故答案为:11.
14.解:360°÷40°=9,
9﹣3=6.
故这个正多边形从一个顶点出发可以作的对角线条数是6.
故答案为:6.
15.解:∵一个正多边形的内角和等于它外角和的2倍,任意多边形的外角和都是360°,
∴这个多边形的内角和是360°×2=720°,
设这个正多边形的边数为n,
则(n﹣2)×180°=720°,
解得n=6,
故这个正多边形每一个内角的大小为720°÷6=120°,
故答案为:120°.
16.解:连接AD,
∵五边形ABCDE是正五边形,
∴∠B=∠BAE=∠E∠EDC=∠C=108°,AE=DE,
∴∠AED=∠EDA=36°,
∴∠BAD=72°,
∵∠BAD+∠ABC=180°,
∴BC∥AD,
∵PQ∥BC,
∴AD∥PQ,
∴∠EPQ=∠EAD=36°,
故答案为:36°.
三.解答题
17.解:(1)设多边形的一个外角为α°,则与其相邻的内角为(3α+20)°,
由题意,得(3α+20)+α=180.
解得α=40,
即多边形的每个外角为40°,
∵多边形的外角和为360°,
∴多边形的边数为360°÷40°=9;
答:这个多边形的边数为9;
(2)这个多边形的内角和为(9﹣2)×180°=1260°,
对角线一共有×(9﹣3)×9=27(条),
答:内角和1260°,对角线27条.
18.解:2100÷180=11,
则正多边形的边数是11+1+2=14边形.
除去的内角的度数为:(14﹣2)×180°﹣2100°=60°.
19.解:(1)∵∠3、∠4、∠5、∠6是四边形的四个内角,
∴∠3+∠4+∠5+∠6=360°,
∴∠3+∠4=360°﹣(∠5+∠6),
∵∠1+∠5=180°,∠2+∠6=180°,
∴∠1+∠2=360°﹣(∠5+∠6),
∴∠1+∠2=∠3+∠4;
(2)四边形的任意两个外角的和等于与它们不相邻的两个内角的和.
20.(1)解:如图1,∵∠2=∠C+∠E,∠1=∠A+∠2,
∴∠A+∠B+∠C+∠D+∠E=∠1+∠B+∠D=180°,
故答案为:180°;
(2)证明:∵∠ABE=∠C+∠E,∠DBC=∠A+∠D,
∠ABE+∠DBE+∠DBC=180°,
∴∠A+∠DBE+∠C+∠D+∠E=180°
∴将图①变形成图②∠A+∠DBE+∠C+∠D+∠E仍然为180°;
(3)证明:∵在△FGD中,∠DFG+∠FGD+∠D=180°,
∠DFG=∠B+∠E,∠FGD=∠A+∠C,
∴∠A+∠B+∠C+∠D+∠E=180°,
∴将图①变形成图③,则∠A+∠B+∠C+∠D+∠E还为180°;
(4)解:∵∠BGF=∠B+∠2=160°,∠2=∠D+∠F,
∴∠B+∠D+∠F=160°,
∵∠BGF=∠1+∠E=160°,∠1=∠A+∠C,
∴∠A+∠C+∠E=160°,
∴∠A+∠B+∠C+∠D+∠E+∠F=320°,
故答案为:320°.
21.解:(1)如图1,∵∠BFG=∠C+∠E,∠BGF=∠A+∠D,
又∵∠B+∠BFG+∠BGF=180°,
∴∠A+∠B+∠C+∠D+∠E=180°;
(2)如图2,∵∠A+∠C=∠1,∠DBE+∠E=∠2,
又∵∠1+∠2+∠D=180°,
∴∠A+∠C+∠DBE+∠E+∠D=180°;
(3)如图3,∵∠B+∠E=∠2,∠A+∠C=∠1,
由三角形内角和定理可知∠1+∠2+∠E=180°,
即∠B+∠D+∠A+∠C+∠E=180°,故结论都成立.
22.解:(1)∵∠B=80°,∠C=70°,
∴∠A=180°﹣(∠B+∠C)=180°﹣(80°+70°)=30°;
(2)如图①,∵把△ADE沿DE折叠,使点A落在四边形BCED所在的平面上,点A的对应点为A',
∴∠A′=∠A=30°,
∴∠3=180°﹣∠A′﹣∠2=150°﹣∠2,
∵∠1+∠3+∠B+∠C=360°,
∴∠1+150°﹣∠2+80°+70°=360°,
∴∠1﹣∠2=60°;
如图②,∵把△ADE沿DE折叠,使点A落在四边形BCED所在的平面上,点A的对应点为A',
∴∠A′=∠A=30°,
∴∠AEA′+∠ADA′=360°﹣∠A﹣∠A′=300°,
∴∠1+∠2=360°﹣∠AEA′﹣∠ADA′=60°;
如图③,方法同①,∠2﹣∠1=60°.
23.解:(1)①∵∠ABC+∠ADC=360°﹣(x+y)=240°,
∴∠MBC+∠NDC=180°﹣∠ABC+180°﹣∠ADC=x+y=120°;
②y﹣x=60°.
理由:如图1,连接BD,
由①有,∠MBC+∠NDC=x+y,
∵BE、DF分别平分四边形的外角∠MBC和∠NDC,
∴∠CBG=∠MBC,∠CDG=∠NDC,
∴∠CBG+∠CDG=∠MBC+∠NDC=(∠MBC+∠NDC)=(x+y),
在△BCD中,∠BDC+∠CBD=180°﹣∠BCD=180°﹣y,
在△BDG中,∠GBD+∠GDB+∠BGD=180°,
∴∠CBG+∠CBD+∠CDG+∠BDC+∠BGD=180°,
∴(∠CBG+∠CDG)+(∠BDC+∠CBD)+∠BGD=180°,
∴(x+y)+180°﹣y+30°=180°,
∴y﹣x=60°;
(2)BE∥DF.
理由:如图2,延长BC交DF于H,
由(1)有,∠MBC+∠NDC=x+y,
∵BE、DF分别平分四边形的外角∠MBC和∠NDC,
∴∠CBE=∠MBC,∠CDH=∠NDC,
∴∠CBE+∠CDH=∠MBC+∠NDC=(∠MBC+∠NDC)=(α+β),
∵∠BCD=∠CDH+∠DHB,
∴∠CDH=∠BCD﹣∠DHB=y﹣∠DHB,
∴∠CBE+y﹣∠DHB=(x+y),
∵x=y,
∴∠CBE+y﹣∠DHB=(y+y)=y,
∴∠CBE=∠DHB,
∴BE∥DF.
