冀教版数学八年级上册课件:13.3全等三角形的判定(共17张PPT)
文档属性
| 名称 | 冀教版数学八年级上册课件:13.3全等三角形的判定(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 162.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-03 21:49:22 | ||
图片预览




文档简介
(共17张PPT)
全等三角形的判定
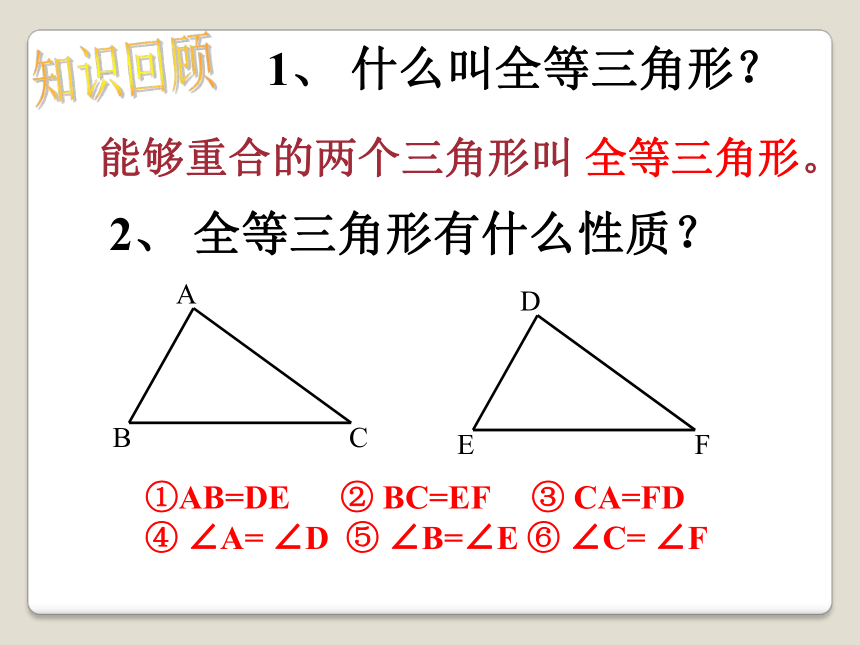
知识回顾
①AB=DE
②
BC=EF
③
CA=FD
④
∠A=
∠D
⑤
∠B=∠E
⑥
∠C=
∠F
A
B
C
D
E
F
1、
什么叫全等三角形?
能够重合的两个三角形叫
全等三角形。
2、
全等三角形有什么性质?
问题一:
根据上面的结论,两个三角形全等,它们的三个角、三条边分别对应相等,那么反过来,如果两个三角形上述六个元素对应相等,是否一定全等?
?
问题二:
两个三角形全等,是否一定需要六个条件呢?如果只满足上述一部分条件,是否我们也能说明他们全等?
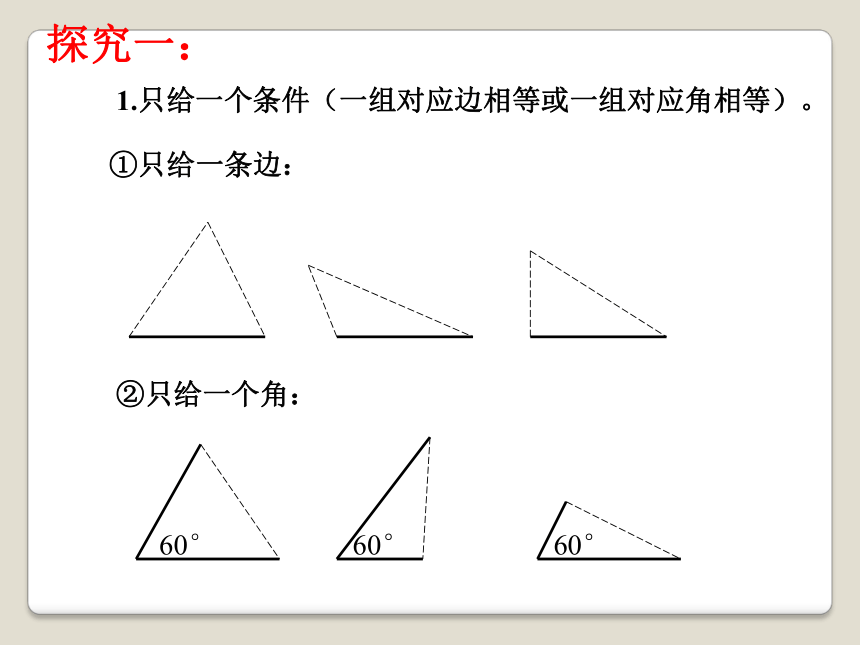
1.只给一个条件(一组对应边相等或一组对应角相等)。
①只给一条边:
②只给一个角:
60°
60°
60°
探究一:
PPT模板:www.1ppt.com/moban/
PPT素材:www.1ppt.com/sucai/
PPT背景:www.1ppt.com/beijing/
PPT图表:www.1ppt.com/tubiao/
PPT下载:www.1ppt.com/xiazai/
PPT教程:
www.1ppt.com/powerpoint/
资料下载:www.1ppt.com/ziliao/
范文下载:www.1ppt.com/fanwen/
试卷下载:www.1ppt.com/shiti/
教案下载:www.1ppt.com/jiaoan/
PPT论坛:www.1ppt.cn
PPT课件:www.1ppt.com/kejian/
语文课件:www.1ppt.com/kejian/yuwen/
数学课件:www.1ppt.com/kejian/shuxue/
英语课件:www.1ppt.com/kejian/yingyu/
美术课件:www.1ppt.com/kejian/meishu/
科学课件:www.1ppt.com/kejian/kexue/
物理课件:www.1ppt.com/kejian/wuli/
化学课件:www.1ppt.com/kejian/huaxue/
生物课件:www.1ppt.com/kejian/shengwu/
地理课件:www.1ppt.com/kejian/dili/
历史课件:www.1ppt.com/kejian/lishi/
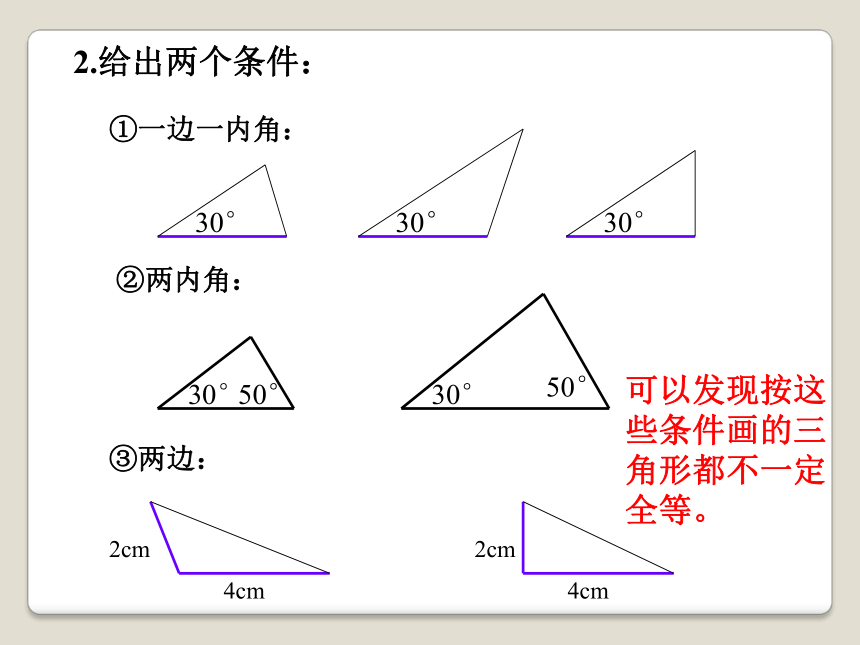
2.给出两个条件:
①一边一内角:
②两内角:
③两边:
30°
30°
30°
30°
30°
50°
50°
2cm
2cm
4cm
4cm
可以发现按这些条件画的三角形都不一定全等。
3.给出三个条件
三条边
三个角
两角一边
两边一角
探究二
你会用刻度尺和圆规画△
DEF吗?
使其三边分别为3cm,4cm和5cm。
把你画的三角形与其他同学所画的三角形剪下来,进行比较,它们能否互相重合?
1、画线段EF=
3cm。
2、分别以E、F为圆心,
5cm
,
4cm
长为半径画两条圆弧,交于点D。
3、连结DE,DF。
△
DEF就是所求的三角形
画法:
有三边对应相等的两个三角形全等.
可以简写成
“边边边”
或“
SSS
”
A
B
C
D
E
F
用
数学语言表述:
在△ABC和△
DEF中
∴
△ABC
≌△
DEF(SSS)
AB=DE
BC=EF
CA=FD
新知学习
判断两个三角形全等的推理过程,叫做证明三角形全等。
C
A
B
D
O
议一议:在下列推理中填写需要补充的条件,使结论成立:
如图,在△AOB和△DOC中
AO=DO(已知)
______=________(已知)
BO=CO(已知)
∴
△AOB≌△DOC(SSS)
解:
△ABC≌△DCB
理由如下:
AB
=
CD
AC
=
DB
=
SSS
2、如图,D、F是线段BC上的两点,
AB=EC,AF=ED,要使△ABF≌△ECD
,
还需要条件
A
E
B
D
F
C
A
B
C
D
想一想
△ABC
≌
(
)
1、如图,AB=CD,AC=BD,△ABC和△DCB是否全等?试说明理由。
△DCB
BC
CB
BF=CD
或
BD=CF
应用迁移,巩固提高
例1.
如下图,△ABC是一个刚架,AB=AC,AD是连接A与BC中点D的支架。
求证:△
ABD≌
△
ACD
分析:要证明△
ABD≌
△
ACD,首先看这两个三角形的三条边是否对应相等。
结论:从这题的证明中可以看出,证明是由题设(已知)出发,经过一步步的推理,最后推出结论正确的过程。
例:如图.
△ABC是一个钢架,AB=AC,AD是连
接A与BC中点D的支架.求证△ABD≌△ACD
A
D
C
B
证明 ∵D是BC的中点
∴BD=CD
在△ABD与△ACD中
AB=AC
BD=CD
AD=AD
∴ △ABD≌△ACD (SSS)
归纳:
①准备条件:证全等时要用的间接条件要先证好;
②三角形全等书写三步骤:
写出在哪两个三角形中
摆出三个条件用大括号括起来
写出全等结论
证明的书写步骤:
(SSS)
A
B
C
D
拓展与提高:如图,在四边形ABCD中
AB=CD,AD=BC,则∠A=
∠C
请说明理由。
解:在
ABD和
CDB中
AB=CD
(已知)
AD=BC
(已知)
BD=DB
(公共边)
∴
ABD
≌
CDB
∴
∠A=
∠C
(
)
全等三角形的对应角相等
已知:
如图,AC=AD
,BC=BD.
求证:
∠C=∠D.
A
B
C
D
解:
在△ACB
和
△ADB中
AC
=
A
D
BC
=
BD
A
B
=
A
B
(公共边)
∴△ACB≌△ADB
(SSS)
议一议:
连结AB
∴∠C=∠D.
(全等三角形对应角相等)
小结
2.
三边对应相等的两个三角形全等
(边边边或SSS);
1.知道三角形三条边的长度怎样画三角形。
3、体验分类讨论的数学思想
4、初步学会理解证明的思路
再
见
全等三角形的判定
知识回顾
①AB=DE
②
BC=EF
③
CA=FD
④
∠A=
∠D
⑤
∠B=∠E
⑥
∠C=
∠F
A
B
C
D
E
F
1、
什么叫全等三角形?
能够重合的两个三角形叫
全等三角形。
2、
全等三角形有什么性质?
问题一:
根据上面的结论,两个三角形全等,它们的三个角、三条边分别对应相等,那么反过来,如果两个三角形上述六个元素对应相等,是否一定全等?
?
问题二:
两个三角形全等,是否一定需要六个条件呢?如果只满足上述一部分条件,是否我们也能说明他们全等?
1.只给一个条件(一组对应边相等或一组对应角相等)。
①只给一条边:
②只给一个角:
60°
60°
60°
探究一:
PPT模板:www.1ppt.com/moban/
PPT素材:www.1ppt.com/sucai/
PPT背景:www.1ppt.com/beijing/
PPT图表:www.1ppt.com/tubiao/
PPT下载:www.1ppt.com/xiazai/
PPT教程:
www.1ppt.com/powerpoint/
资料下载:www.1ppt.com/ziliao/
范文下载:www.1ppt.com/fanwen/
试卷下载:www.1ppt.com/shiti/
教案下载:www.1ppt.com/jiaoan/
PPT论坛:www.1ppt.cn
PPT课件:www.1ppt.com/kejian/
语文课件:www.1ppt.com/kejian/yuwen/
数学课件:www.1ppt.com/kejian/shuxue/
英语课件:www.1ppt.com/kejian/yingyu/
美术课件:www.1ppt.com/kejian/meishu/
科学课件:www.1ppt.com/kejian/kexue/
物理课件:www.1ppt.com/kejian/wuli/
化学课件:www.1ppt.com/kejian/huaxue/
生物课件:www.1ppt.com/kejian/shengwu/
地理课件:www.1ppt.com/kejian/dili/
历史课件:www.1ppt.com/kejian/lishi/
2.给出两个条件:
①一边一内角:
②两内角:
③两边:
30°
30°
30°
30°
30°
50°
50°
2cm
2cm
4cm
4cm
可以发现按这些条件画的三角形都不一定全等。
3.给出三个条件
三条边
三个角
两角一边
两边一角
探究二
你会用刻度尺和圆规画△
DEF吗?
使其三边分别为3cm,4cm和5cm。
把你画的三角形与其他同学所画的三角形剪下来,进行比较,它们能否互相重合?
1、画线段EF=
3cm。
2、分别以E、F为圆心,
5cm
,
4cm
长为半径画两条圆弧,交于点D。
3、连结DE,DF。
△
DEF就是所求的三角形
画法:
有三边对应相等的两个三角形全等.
可以简写成
“边边边”
或“
SSS
”
A
B
C
D
E
F
用
数学语言表述:
在△ABC和△
DEF中
∴
△ABC
≌△
DEF(SSS)
AB=DE
BC=EF
CA=FD
新知学习
判断两个三角形全等的推理过程,叫做证明三角形全等。
C
A
B
D
O
议一议:在下列推理中填写需要补充的条件,使结论成立:
如图,在△AOB和△DOC中
AO=DO(已知)
______=________(已知)
BO=CO(已知)
∴
△AOB≌△DOC(SSS)
解:
△ABC≌△DCB
理由如下:
AB
=
CD
AC
=
DB
=
SSS
2、如图,D、F是线段BC上的两点,
AB=EC,AF=ED,要使△ABF≌△ECD
,
还需要条件
A
E
B
D
F
C
A
B
C
D
想一想
△ABC
≌
(
)
1、如图,AB=CD,AC=BD,△ABC和△DCB是否全等?试说明理由。
△DCB
BC
CB
BF=CD
或
BD=CF
应用迁移,巩固提高
例1.
如下图,△ABC是一个刚架,AB=AC,AD是连接A与BC中点D的支架。
求证:△
ABD≌
△
ACD
分析:要证明△
ABD≌
△
ACD,首先看这两个三角形的三条边是否对应相等。
结论:从这题的证明中可以看出,证明是由题设(已知)出发,经过一步步的推理,最后推出结论正确的过程。
例:如图.
△ABC是一个钢架,AB=AC,AD是连
接A与BC中点D的支架.求证△ABD≌△ACD
A
D
C
B
证明 ∵D是BC的中点
∴BD=CD
在△ABD与△ACD中
AB=AC
BD=CD
AD=AD
∴ △ABD≌△ACD (SSS)
归纳:
①准备条件:证全等时要用的间接条件要先证好;
②三角形全等书写三步骤:
写出在哪两个三角形中
摆出三个条件用大括号括起来
写出全等结论
证明的书写步骤:
(SSS)
A
B
C
D
拓展与提高:如图,在四边形ABCD中
AB=CD,AD=BC,则∠A=
∠C
请说明理由。
解:在
ABD和
CDB中
AB=CD
(已知)
AD=BC
(已知)
BD=DB
(公共边)
∴
ABD
≌
CDB
∴
∠A=
∠C
(
)
全等三角形的对应角相等
已知:
如图,AC=AD
,BC=BD.
求证:
∠C=∠D.
A
B
C
D
解:
在△ACB
和
△ADB中
AC
=
A
D
BC
=
BD
A
B
=
A
B
(公共边)
∴△ACB≌△ADB
(SSS)
议一议:
连结AB
∴∠C=∠D.
(全等三角形对应角相等)
小结
2.
三边对应相等的两个三角形全等
(边边边或SSS);
1.知道三角形三条边的长度怎样画三角形。
3、体验分类讨论的数学思想
4、初步学会理解证明的思路
再
见
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
