2020-2021学年第一学期苏科版七年级数学上册第6章平面图形的认识(一) 综合 培优训练卷(1)(word有答案)
文档属性
| 名称 | 2020-2021学年第一学期苏科版七年级数学上册第6章平面图形的认识(一) 综合 培优训练卷(1)(word有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 202.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-04 12:58:08 | ||
图片预览


文档简介
2020-2021苏科版七年级数学上册第6章平面图形的认识(一)
综合培优训练卷(1)
一、选择题
1、如图,下列不正确的几何语句是(
)
A.直线AB与直线BA是同一条直线
B.射线OA与射线OB是同一条射线
C.射线OA与射线AB是同一条射线
D.线段AB与线段BA是同一条线段
2、下列语句:①一条直线有且只有一条垂线;②不相等的两个角一定不是对顶角;
③两条不相交的直线叫做平行线;
④若两个角的一对边在同一直线上,另一对边互相平行,则这两个角相等;
⑤不在同一直线上的四个点可画6条直线;
⑥如果两个角是邻补角,那么这两个角的平分线组成的图形是直角.
其中错误的有(
)
A.2个
B.3个
C.4个
D.5个
3、如图,B是线段AD的中点,C是BD上一点,则下列结论中错误的是(
)
A.BC=AB-CD
B.BC=AD-CD
C.BC=(AD+CD)
D.BC=AC-BD
4、当时钟指向上午10:10分,时针与分针的夹角是多少度( )
A.115°
B.120°
C.105°
D.90°
5、一个角的补角比这个角的余角的3倍少20°,这个角的度数是( )
A.30°
B.35°
C.40°
D.45°
6、如果∠α与∠β是邻补角,且∠α>∠β,那么∠β的余角是(
)
A.(∠α+∠β)
B.∠α
C.(∠α-∠β)
D.不能确定
7、如果∠1与∠2互补,∠2与∠3互余,则∠1与∠3的关系是(
)
A.∠1=∠3
B.∠1=180°-∠3
C.∠1=90°+∠3
D.以上都不对
8、下列说法正确的是(
)
A.在同一平面内,不相交的两条线段平行
B.
在同一平面内,不相交的两条射线平行
C.
不相交的直线一定是平行线
D.
在同一平面内,两条直线的关系只有两种:平行或相交
9、如图,已知ON⊥L,OM⊥L,所以OM与ON重合,其理由是(
)
A.两点确定一条直线
B.在同一平面内,经过一点有且只有一条直线与已知直线垂直
C.在同一平面内,过一点只能作一条垂线
D.垂线段最短
10、如图,把水渠中的水引到水池C,先过C点向渠岸AB画垂线,垂足为点D,再沿垂线CD开沟才能使沟最短,其依据是
(
)
A.垂线最短
B.过一点确定一条直线与已知直线垂直
C.垂线段最短
D.以上说法都不对
11、如图,点A在直线l1上,点B,C在直线l2上,AB⊥l2,AC⊥l1,AB=4,BC=3,AC=5,有下列说法:
(1)点B到直线l1的距离等于4
(2)点C到直线l1的距离等于5
(3)点A到直线l2间的距离等于4
(4)点B到直线AC的距离等于3
其中正确的说法有(
)
A.1个
B.2个
C.3个
D.4个
12、如图,C、D在线段BE上,下列说法:①直线CD上以B、C、D、E为端点的线段共有6条;
②图中有2对互补的角;③若∠BAE=90°,∠DAC=40°,则以A为顶点的所有小于平角的角的度数和为360°;④若BC=2,CD=DE=3,点F是线段BE上任意一点,则点F到点B、C、D、E的距离之和最大值为15,最小值为11,其中说法正确的个数有( )
A.1个
B.2个
C.3个
D.4个
二、填空题
13、已知线段AB=1
996
cm,P、Q是线段AB上的两个点,线段AQ=1
200
cm,线段BP=1
050
cm,
则线段PQ=___________.
14、已知线段AB=10
cm,BC=5
cm,A、B、C三点在同一条直线上,则AC=_
_.
15、如图,线段AB=BC=CD=DE=1
cm,那么图中所有线段的长度之和等于________cm.
16、如图,点O是直线AD上一点,射线OC、OE分别是∠AOB、∠BOD的平分线,若∠AOC=28°,
则∠COD=_________,∠BOE=__________.
17、如图,将一副三角板叠放在一起,使直角的顶点重合于点O,则∠AOB+∠DOC=
°
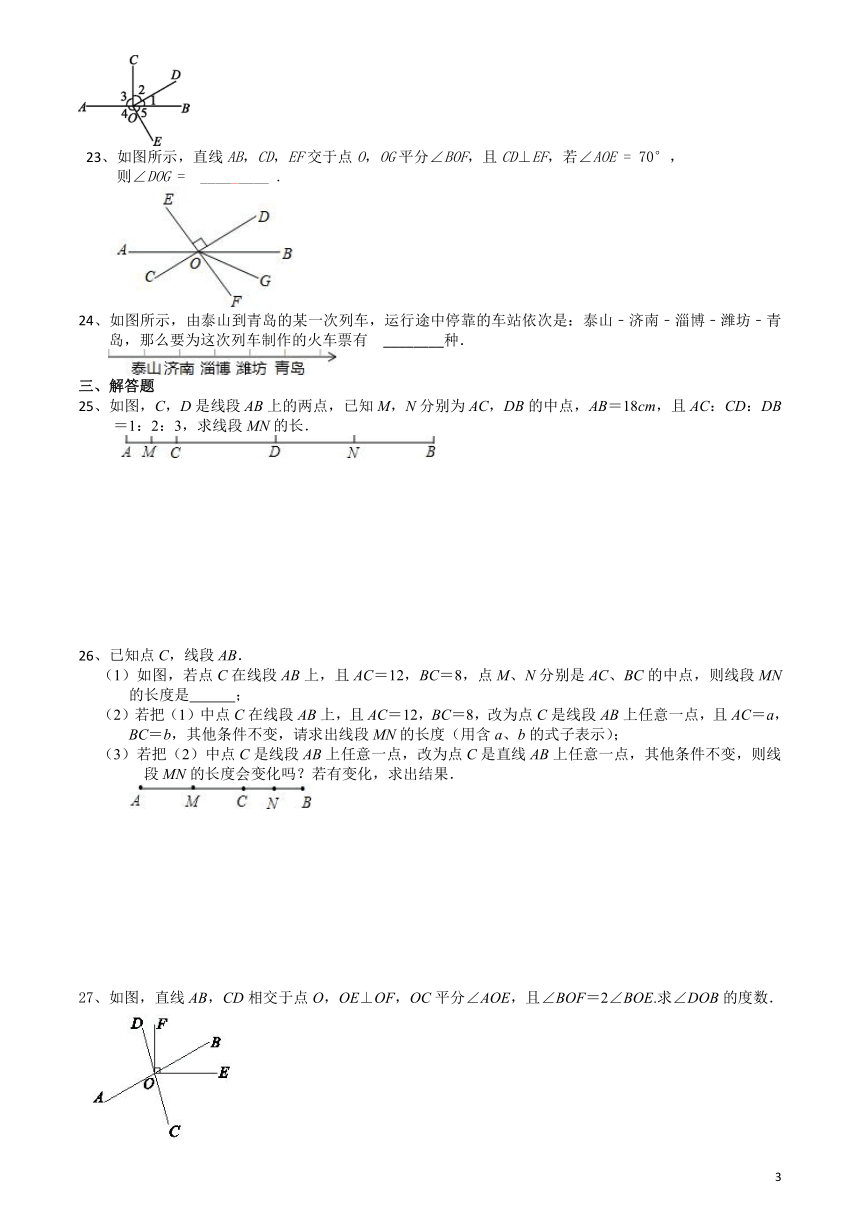
18、如图,直线AB,CD,EF交于点O,OG平分∠BOF,且CD⊥EF,∠AOE=70°,则∠DOG=________°.
19、如图,OM平分∠AOB,ON平分∠COD.若∠MON=50°,∠BOC=10°,则∠AOD=
__________.
19、35.15°=
°
′
″;12°15′36″=
°.
20、已知射线OA,从O点再引射线OB,OC,使∠AOB=67°31′,∠BOC=48°39′,
则∠AOC的度数为
21、如图,将一张长方形纸片ABCD分别沿着BE、BF折叠,使边AB、CB均落在BD上,得到折痕BE、BF,则∠ABE+∠CBF=
.
22、如图,O是直线AB上的一点,OC,OD,OE是从点O引出的三条射线,
且∠1∶∠2∶∠3∶∠4=1∶2∶3∶4,则∠5= °.?
23、如图所示,直线AB,CD,EF交于点O,OG平分∠BOF,且CD⊥EF,若∠AOE
=
70°,
则∠DOG
=
_________
.
24、如图所示,由泰山到青岛的某一次列车,运行途中停靠的车站依次是:泰山﹣济南﹣淄博﹣潍坊﹣青岛,那么要为这次列车制作的火车票有
________种.
三、解答题
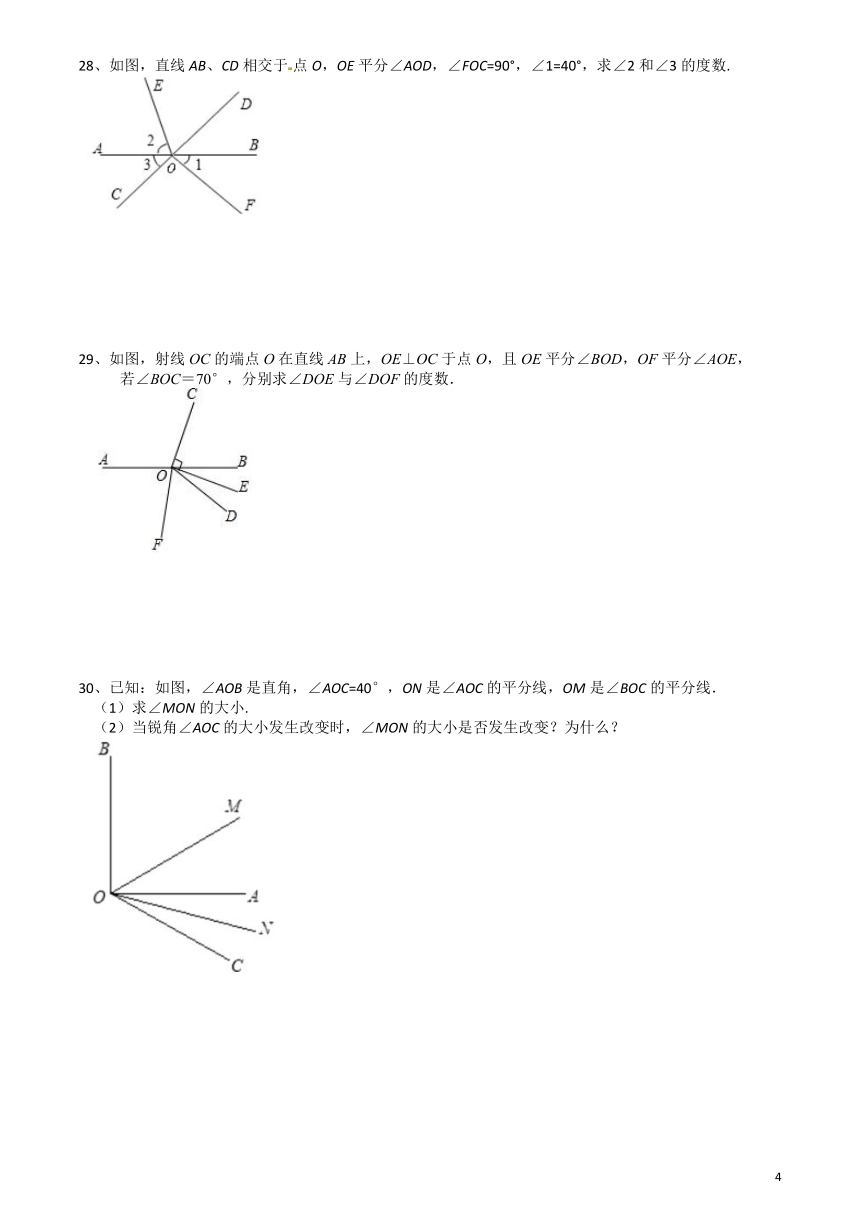
25、如图,C,D是线段AB上的两点,已知M,N分别为AC,DB的中点,AB=18cm,且AC:CD:DB=1:2:3,求线段MN的长.
26、已知点C,线段AB.
(1)如图,若点C在线段AB上,且AC=12,BC=8,点M、N分别是AC、BC的中点,则线段MN的长度是
;
(2)若把(1)中点C在线段AB上,且AC=12,BC=8,改为点C是线段AB上任意一点,且AC=a,BC=b,其他条件不变,请求出线段MN的长度(用含a、b的式子表示);
(3)若把(2)中点C是线段AB上任意一点,改为点C是直线AB上任意一点,其他条件不变,则线段MN的长度会变化吗?若有变化,求出结果.
27、如图,直线AB,CD相交于点O,OE⊥OF,OC平分∠AOE,且∠BOF=2∠BOE.求∠DOB的度数.
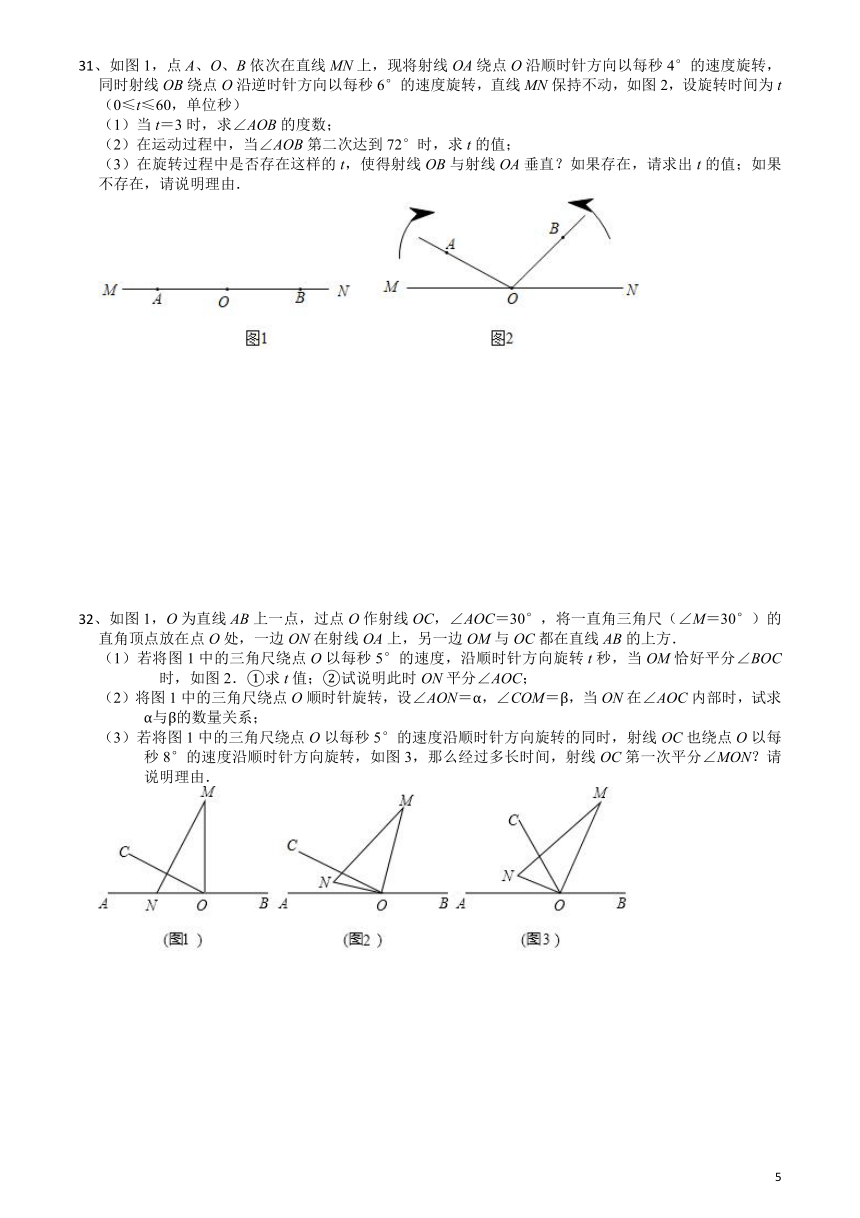
28、如图,直线AB、CD相交于点O,OE平分∠AOD,∠FOC=90°,∠1=40°,求∠2和∠3的度数.
29、如图,射线OC的端点O在直线AB上,OE⊥OC于点O,且OE平分∠BOD,OF平分∠AOE,
若∠BOC=70°,分别求∠DOE与∠DOF的度数.
30、已知:如图,∠AOB是直角,∠AOC=40°,ON是∠AOC的平分线,OM是∠BOC的平分线.
(1)求∠MON的大小.
(2)当锐角∠AOC的大小发生改变时,∠MON的大小是否发生改变?为什么?
31、如图1,点A、O、B依次在直线MN上,现将射线OA绕点O沿顺时针方向以每秒4°的速度旋转,同时射线OB绕点O沿逆时针方向以每秒6°的速度旋转,直线MN保持不动,如图2,设旋转时间为t(0≤t≤60,单位秒)
(1)当t=3时,求∠AOB的度数;
(2)在运动过程中,当∠AOB第二次达到72°时,求t的值;
(3)在旋转过程中是否存在这样的t,使得射线OB与射线OA垂直?如果存在,请求出t的值;如果不存在,请说明理由.
32、如图1,O为直线AB上一点,过点O作射线OC,∠AOC=30°,将一直角三角尺(∠M=30°)的直角顶点放在点O处,一边ON在射线OA上,另一边OM与OC都在直线AB的上方.
(1)若将图1中的三角尺绕点O以每秒5°的速度,沿顺时针方向旋转t秒,当OM恰好平分∠BOC时,如图2.①求t值;②试说明此时ON平分∠AOC;
(2)将图1中的三角尺绕点O顺时针旋转,设∠AON=α,∠COM=β,当ON在∠AOC内部时,试求α与β的数量关系;
(3)若将图1中的三角尺绕点O以每秒5°的速度沿顺时针方向旋转的同时,射线OC也绕点O以每秒8°的速度沿顺时针方向旋转,如图3,那么经过多长时间,射线OC第一次平分∠MON?请说明理由.
2020-2021苏科版七年级数学上册第6章平面图形的认识(一)
综合
培优训练卷(1)(答案)
一、选择题
1、如图,下列不正确的几何语句是(
)
A.直线AB与直线BA是同一条直线
B.射线OA与射线OB是同一条射线
C.射线OA与射线AB是同一条射线
D.线段AB与线段BA是同一条线段
解析:射线OA与射线AB不是同一条射线,因为端点不同.故选C
2、下列语句:①一条直线有且只有一条垂线;②不相等的两个角一定不是对顶角;
③两条不相交的直线叫做平行线;
④若两个角的一对边在同一直线上,另一对边互相平行,则这两个角相等;
⑤不在同一直线上的四个点可画6条直线;
⑥如果两个角是邻补角,那么这两个角的平分线组成的图形是直角.
其中错误的有(
)
A.2个
B.3个
C.4个
D.5个
解析:①一条直线有无数条垂线,故①错误;
②不相等的两个角一定不是对顶角,故②正确;
③在同一平面内,两条不相交的直线叫做平行线,故③错误;
④若两个角的一对边在同一直线上,另一对边互相平行,则这两个角相等或互补,故④错误;
⑤不在同一直线上的四个点可画4或6条直线,故⑤错误;
⑥如果两个角是邻补角,那么这两个角的平分线组成的图形是直角,故⑥正确.
所以错误的有4个,故选C.
3、如图,B是线段AD的中点,C是BD上一点,则下列结论中错误的是(
)
A.BC=AB-CD
B.BC=AD-CD
C.BC=(AD+CD)
D.BC=AC-BD
解析:∵
B是线段AD的中点,∴
AB=BD=AD.
A.BC=BD-CD=AB-CD,故本选项正确;
B.BC=BD-CD=AD-CD,故本选项正确;
D.BC=AC-AB=AC-BD,故本选项正确.只有C选项是错误的.
4、当时钟指向上午10:10分,时针与分针的夹角是多少度( )
A.115°
B.120°
C.105°
D.90°
【解答】解:时钟指向上午10:10分,时针与分针相距3份,
时钟指向上午10:10分,时针与分针的夹角是多少度30°115°,
或时针与分针的夹角是120°﹣10×()°=115°;
故选:A.
5、一个角的补角比这个角的余角的3倍少20°,这个角的度数是( )
A.30°
B.35°
C.40°
D.45°
【解答】解:设这个角为α,则它的补角为180°﹣α,余角为90°﹣α,
根据题意得,180°﹣α=3(90°﹣α)﹣20°,
解得α=35°.
故选:B.
6、如果∠α与∠β是邻补角,且∠α>∠β,那么∠β的余角是(
)
A.(∠α+∠β)
B.∠α
C.(∠α-∠β)
D.不能确定
解析:因为∠α与∠β是邻补角,所以∠α+∠β=180°,(∠α+∠β)=90°.
所以∠β的余角是90°-∠β=(∠α+∠β)-∠β=(∠α-∠β),故选C.
7、如果∠1与∠2互补,∠2与∠3互余,则∠1与∠3的关系是(
)
A.∠1=∠3
B.∠1=180°-∠3
C.∠1=90°+∠3
D.以上都不对
解析:∵
∠1+∠2=180°,∴
∠1=180°-∠2.
又∵
∠2+∠3=90°,∴
∠3=90°-∠2.
∴
∠1-∠3=90°,即∠1=90°+∠3,故选C.
8、下列说法正确的是(
)
A.在同一平面内,不相交的两条线段平行
B.
在同一平面内,不相交的两条射线平行
C.
不相交的直线一定是平行线
D.
在同一平面内,两条直线的关系只有两种:平行或相交
答案:D
9、如图,已知ON⊥L,OM⊥L,所以OM与ON重合,其理由是(
B
)
A.两点确定一条直线
B.在同一平面内,经过一点有且只有一条直线与已知直线垂直
C.在同一平面内,过一点只能作一条垂线
D.垂线段最短
10、如图,把水渠中的水引到水池C,先过C点向渠岸AB画垂线,垂足为点D,再沿垂线CD开沟才能使沟最短,其依据是
(
)
A.垂线最短
B.过一点确定一条直线与已知直线垂直
C.垂线段最短
D.以上说法都不对
答案:C
“垂线”是直线,不可度量;“垂线段”是线段,可以度量。
11、如图,点A在直线l1上,点B,C在直线l2上,AB⊥l2,AC⊥l1,AB=4,BC=3,AC=5,有下列说法:
(1)点B到直线l1的距离等于4
(2)点C到直线l1的距离等于5
(3)点A到直线l2间的距离等于4
(4)点B到直线AC的距离等于3
其中正确的说法有(
)
A.1个
B.2个
C.3个
D.4个
答案:B
由点到直线的距离的定义可知,只有说法(2)、(3)正确
12、如图,C、D在线段BE上,下列说法:①直线CD上以B、C、D、E为端点的线段共有6条;
②图中有2对互补的角;③若∠BAE=90°,∠DAC=40°,则以A为顶点的所有小于平角的角的度数和为360°;④若BC=2,CD=DE=3,点F是线段BE上任意一点,则点F到点B、C、D、E的距离之和最大值为15,最小值为11,其中说法正确的个数有( )
A.1个
B.2个
C.3个
D.4个
【解析】①以B、C、D、E为端点的线段BC、BD、BE、CE、CD、DE共6条,故①正确;
②图中互补的角就是分别以C、D为顶点的两对邻补角,即∠BCA和∠ACD互补,∠ADE和∠ADC互补,故②正确;
③由∠BAE=90°,∠CAD=40°,根据图形可以求出
∠BAC+∠DAE+∠DAC+∠BAE+∠BAD+∠CAE=90°+90°+90°+40°=310°,故③错误;
④当F在线段CD上,则点F到点B、C、D、E的距离之和最小为FB+FE+FD+FC=11,当F和E重合,则点F到点B、C、D、E的距离之和最大为FB+FE+FD+FC=8+0+6+3=17,故④错误.
故选B.
二、填空题
13、已知线段AB=1
996
cm,P、Q是线段AB上的两个点,线段AQ=1
200
cm,线段BP=1
050
cm,
则线段PQ=___________.
解析:如图,由题意得:AQ+BP=AB+PQ=1
200+1
050=2
250(cm),
∴
PQ=2
250-1
996=254(cm).
14、已知线段AB=10
cm,BC=5
cm,A、B、C三点在同一条直线上,则AC=_
_.
解析:本题有两种情形:
(1)当点C在线段AB上时,如图,有AC=AB-BC,
又∵
AB=10
cm,BC=5
cm,∴
AC=10-5=5(cm);
(2)当点C在线段AB的延长线上时,如图,有AC=AB+BC,
又∵
AB=10
cm,BC=5
cm,∴
AC=10+5=15(cm).
故线段AC=5
cm或15
cm.
15、如图,线段AB=BC=CD=DE=1
cm,那么图中所有线段的长度之和等于________cm.
解析:因为长为1
cm的线段共4条,长为2
cm的线段共3条,长为3
cm的线段共2条,长为4
cm的线段仅1条,
所以图中所有线段长度之和为1×4+2×3+3×2+4×1=20(cm).
16、如图,点O是直线AD上一点,射线OC、OE分别是∠AOB、∠BOD的平分线,若∠AOC=28°,
则∠COD=_________,∠BOE=__________.
解析:∵
∠AOC+∠COD=180°,∠AOC=28°,∴
∠COD=152°.
∵
OC是∠AOB的平分线,∠AOC=28°,∴
∠AOB=2∠AOC=2×28°=56°,
∴
∠BOD=180°-∠AOB=180°-56°=124°.
∵
OE是∠BOD的平分线,∴
∠BOE=∠BOD=×124°=62°.
17、如图,将一副三角板叠放在一起,使直角的顶点重合于点O,则∠AOB+∠DOC=
180
°
18、如图,直线AB,CD,EF交于点O,OG平分∠BOF,且CD⊥EF,∠AOE=70°,则∠DOG=________°.
答案:因为∠BOF=∠AOE=70°,所以∠BOG==35°,所以∠DOG=∠BOD+∠BOG=55°。
19、如图,OM平分∠AOB,ON平分∠COD.若∠MON=50°,∠BOC=10°,则∠AOD=
__________.
解析:∵
OM平分∠AOB,ON平分∠COD,
∴
∠AOM=∠BOM,∠CON=∠DON.
∵
∠MON=50°,∠BOC=10°,
∴
∠MON-∠BOC
=40°,即∠BOM+∠CON=40°.
∴
∠AOD=∠MON+∠AOM+∠DON=∠MON+∠BOM+∠CON=50°+40°=90°.
19、35.15°=
°
′
″;12°15′36″=
°.
【解答】解:∵0.15°=9′,∴35.15°=35°9′;
∵36″=0.6′,15.6′=0.26°,∴12°15′36″=12.26°,
故答案为:35,9,0;12.26.
20、已知射线OA,从O点再引射线OB,OC,使∠AOB=67°31′,∠BOC=48°39′,
则∠AOC的度数为
【解析】如右图所示,
①OC在OA、OB之间,∵∠AOB=67°31′,∠BOC=48°39′,
∴∠AOC=∠AOB﹣∠BOC=67°31′﹣48°39′=66°91′﹣48°39′=18°52′;
②OB在OA、OC之间,
∵∠AOB=67°31′,∠BOC=48°39′,
∴∠AOC=∠AOB+∠BOC=67°31′+48°39′=115°70′=116°10′;
故答案是18°52′或116°10′.
21、如图,将一张长方形纸片ABCD分别沿着BE、BF折叠,使边AB、CB均落在BD上,得到折痕BE、BF,则∠ABE+∠CBF=
.
【解析】由折叠得,∠ABE=∠DBE,∠CBF=∠DBF,
∵∠ABE+∠DBE+∠CBF+∠DBF=∠ABC=90°,
∴∠ABE+∠CBF=∠ABC=×90°=45°,
故答案为45°.
22、如图,O是直线AB上的一点,OC,OD,OE是从点O引出的三条射线,
且∠1∶∠2∶∠3∶∠4=1∶2∶3∶4,则∠5= °.?
[解析]
设∠1=x°,则∠2=2x°,∠3=3x°.依题意,得x+2x+3x=180,解得x=30,
所以∠4=4x°=120°,∠5=180°-120°=60°.
23、如图所示,直线AB,CD,EF交于点O,OG平分∠BOF,且CD⊥EF,若∠AOE
=
70°,
则∠DOG
=
____55_____
.
24、如图所示,由泰山到青岛的某一次列车,运行途中停靠的车站依次是:泰山﹣济南﹣淄博﹣潍坊﹣青岛,那么要为这次列车制作的火车票有
________种.
【解析】解:如图,设泰山﹣﹣济南﹣﹣淄博﹣﹣潍坊﹣﹣青岛五站分别用A、B、C、D、E表示,
则共有线段:AB、AC、AD、AE、BC、BD、BE、CD、CE、DE共10条,
所以,需要制作火车票10×2=20种.
故答案为:20.
三、解答题
25、如图,C,D是线段AB上的两点,已知M,N分别为AC,DB的中点,AB=18cm,且AC:CD:DB=1:2:3,求线段MN的长.
【解答】解:设AC,CD,DB的长分别为xcm,2xcm,3xcm
∵AC+CD+DB=AB,AB=18cm,
∴x+2x+3x=18,
解得x=3
∴AC=3cm,CD=6cm,DB=9cm
∵M,N为AC,DB的中点,
∴
∴MN=MC+CD+DN=12cm,
∴MN的长为12cm.
26、已知点C,线段AB.
(1)如图,若点C在线段AB上,且AC=12,BC=8,点M、N分别是AC、BC的中点,则线段MN的长度是
;
(2)若把(1)中点C在线段AB上,且AC=12,BC=8,改为点C是线段AB上任意一点,且AC=a,BC=b,其他条件不变,请求出线段MN的长度(用含a、b的式子表示);
(3)若把(2)中点C是线段AB上任意一点,改为点C是直线AB上任意一点,其他条件不变,则线段MN的长度会变化吗?若有变化,求出结果.
【解答】解:(1)点M、N分别是AC、BC的中点,AC=12,BC=8,
MC=AC÷2=12÷2=6,
NC=CB÷2=8÷2=4,
由线段的和差,得MN=MC+NC=6+4=10.
答:线段MN的长是10,
故答案为:10;
(2)由点M、N分别是AC、BC的中点,可得,
所以
(3)线段MN的长度会变化
当点C在线段AB上时,由(2)知
当点C在线段AB上的延长线时,如图,
则AC>BC,即a>b.
由点M、N分别是AC、BC的中点.
可得,.
所以.
当点C在线段BA上的延长线时,如图.
则BC>AC,即b>a.
由点M、N分别是AC、BC的中点.可得,.
所以.
27、如图,直线AB,CD相交于点O,OE⊥OF,OC平分∠AOE,且∠BOF=2∠BOE.求∠DOB的度数.
解:因为OE⊥OF,所以∠EOF=90°.
因为∠BOF=2∠BOE,所以3∠BOE=90°,即∠BOE=30°,所以∠AOE=180°-∠BOE=150°.
因为OC平分∠AOE,所以∠AOC=∠AOE=75°,所以∠DOB=∠AOC=75°.
28、如图,直线AB、CD相交于点O,OE平分∠AOD,∠FOC=90°,∠1=40°,求∠2和∠3的度数.
解:∵
∠FOC=90°,∠1=40°,AB为直线,
∴
∠3+∠FOC+∠1=180°,
∴
∠3=180°-90°-40°=50°.
∵
∠3与∠AOD互补,∴
∠AOD=180°-∠3=130°.
∵
OE平分∠AOD,
∴
∠2=∠AOD=65°.
29、如图,射线OC的端点O在直线AB上,OE⊥OC于点O,且OE平分∠BOD,OF平分∠AOE,
若∠BOC=70°,分别求∠DOE与∠DOF的度数.
【解答】解:∵OE⊥OC于点O,∴∠COE=90°,
∵∠BOC=70°,∴∠BOE=∠COE﹣∠BOC=90°﹣70°=20°,
∵OE平分∠BOD,∴∠DOE=∠BOE=20°,
∵∠AOB=180°,∴∠AOE=180°﹣∠BOE=180°﹣20°=160°,
∵OF平分∠AOE,∴∠EOF∠AOE=80°,∴∠DOF=∠EOF﹣∠DOE=80°﹣20°=60°,
综上,∠DOE的度数为20°,∠DOF的度数为60°.
30、已知:如图,∠AOB是直角,∠AOC=40°,ON是∠AOC的平分线,OM是∠BOC的平分线.
(1)求∠MON的大小.
(2)当锐角∠AOC的大小发生改变时,∠MON的大小是否发生改变?为什么?
解:(1)∵
∠AOB是直角,∠AOC=40°,∴
∠AOB+∠AOC=90°+40°=130°.
∵
OM是∠BOC的平分线,ON是∠AOC的平分线,
∴
∠MOC=∠BOC=65°,∠NOC=∠AOC=20°.
∴
∠MON=∠MOC-∠NOC=65°-20°=45°.
(2)当锐角∠AOC的大小发生改变时,∠MON的大小不发生改变.
∵
∠MON=∠MOC-∠NOC=∠BOC-∠AOC=(∠BOC-∠AOC)=∠AOB,
又∠AOB=90°,∴
∠MON=∠AOB=45°.
31、如图1,点A、O、B依次在直线MN上,现将射线OA绕点O沿顺时针方向以每秒4°的速度旋转,同时射线OB绕点O沿逆时针方向以每秒6°的速度旋转,直线MN保持不动,如图2,设旋转时间为t(0≤t≤60,单位秒)
(1)当t=3时,求∠AOB的度数;
(2)在运动过程中,当∠AOB第二次达到72°时,求t的值;
(3)在旋转过程中是否存在这样的t,使得射线OB与射线OA垂直?如果存在,请求出t的值;如果不存在,请说明理由.
【解答】解:(1)当t=3时,∠AOB=180°﹣4°×3﹣6°×3=150°.
(2)依题意,得:4t+6t=180+72,解得:t.
答:当∠AOB第二次达到72°时,t的值为.
(3)当0≤t≤18时,180﹣4t﹣6t=90,解得:t=9;
当18≤t≤60时,4t+6t=180+90或4t+6t=180+270,解得:t=27或t=45.
答:在旋转过程中存在这样的t,使得射线OB与射线OA垂直,t的值为9、27或45.
32、如图1,O为直线AB上一点,过点O作射线OC,∠AOC=30°,将一直角三角尺(∠M=30°)的直角顶点放在点O处,一边ON在射线OA上,另一边OM与OC都在直线AB的上方.
(1)若将图1中的三角尺绕点O以每秒5°的速度,沿顺时针方向旋转t秒,当OM恰好平分∠BOC时,如图2.①求t值;②试说明此时ON平分∠AOC;
(2)将图1中的三角尺绕点O顺时针旋转,设∠AON=α,∠COM=β,当ON在∠AOC内部时,试求α与β的数量关系;
(3)若将图1中的三角尺绕点O以每秒5°的速度沿顺时针方向旋转的同时,射线OC也绕点O以每秒8°的速度沿顺时针方向旋转,如图3,那么经过多长时间,射线OC第一次平分∠MON?请说明理由.
【解答】解:(1)①如图2中,∵∠AOC=30°,∴∠BOC=180°﹣∠AOC=150°,
∵OM平分∠BOC,∴∠COM=∠BOM∠BOC=75°,∠AON=180°﹣90°﹣75°=15°,
∴t3s,
②当t=3时,∠AON=3t=15°,∠CON=30°﹣3t=15°,∴∠AON=∠CON,
∴ON平分∠AOC;
(2)∵∠CON=30°﹣α=90°﹣β,∴β=α+60°;
(3)∵OC平分∠MON,∠MON=90°,∴∠CON=∠COM=45°,
∵三角板绕点O以每秒5°的速度,射线OC也绕O点以每秒8°的速度沿顺时针方向旋转一周,
∴设∠AON=5t,∠AOC=30+8t,
∵∠AOC﹣∠AON=∠CON,∴30+8t﹣5t=45,解得t=5,
∴经过5秒OC平分∠MON.
综合培优训练卷(1)
一、选择题
1、如图,下列不正确的几何语句是(
)
A.直线AB与直线BA是同一条直线
B.射线OA与射线OB是同一条射线
C.射线OA与射线AB是同一条射线
D.线段AB与线段BA是同一条线段
2、下列语句:①一条直线有且只有一条垂线;②不相等的两个角一定不是对顶角;
③两条不相交的直线叫做平行线;
④若两个角的一对边在同一直线上,另一对边互相平行,则这两个角相等;
⑤不在同一直线上的四个点可画6条直线;
⑥如果两个角是邻补角,那么这两个角的平分线组成的图形是直角.
其中错误的有(
)
A.2个
B.3个
C.4个
D.5个
3、如图,B是线段AD的中点,C是BD上一点,则下列结论中错误的是(
)
A.BC=AB-CD
B.BC=AD-CD
C.BC=(AD+CD)
D.BC=AC-BD
4、当时钟指向上午10:10分,时针与分针的夹角是多少度( )
A.115°
B.120°
C.105°
D.90°
5、一个角的补角比这个角的余角的3倍少20°,这个角的度数是( )
A.30°
B.35°
C.40°
D.45°
6、如果∠α与∠β是邻补角,且∠α>∠β,那么∠β的余角是(
)
A.(∠α+∠β)
B.∠α
C.(∠α-∠β)
D.不能确定
7、如果∠1与∠2互补,∠2与∠3互余,则∠1与∠3的关系是(
)
A.∠1=∠3
B.∠1=180°-∠3
C.∠1=90°+∠3
D.以上都不对
8、下列说法正确的是(
)
A.在同一平面内,不相交的两条线段平行
B.
在同一平面内,不相交的两条射线平行
C.
不相交的直线一定是平行线
D.
在同一平面内,两条直线的关系只有两种:平行或相交
9、如图,已知ON⊥L,OM⊥L,所以OM与ON重合,其理由是(
)
A.两点确定一条直线
B.在同一平面内,经过一点有且只有一条直线与已知直线垂直
C.在同一平面内,过一点只能作一条垂线
D.垂线段最短
10、如图,把水渠中的水引到水池C,先过C点向渠岸AB画垂线,垂足为点D,再沿垂线CD开沟才能使沟最短,其依据是
(
)
A.垂线最短
B.过一点确定一条直线与已知直线垂直
C.垂线段最短
D.以上说法都不对
11、如图,点A在直线l1上,点B,C在直线l2上,AB⊥l2,AC⊥l1,AB=4,BC=3,AC=5,有下列说法:
(1)点B到直线l1的距离等于4
(2)点C到直线l1的距离等于5
(3)点A到直线l2间的距离等于4
(4)点B到直线AC的距离等于3
其中正确的说法有(
)
A.1个
B.2个
C.3个
D.4个
12、如图,C、D在线段BE上,下列说法:①直线CD上以B、C、D、E为端点的线段共有6条;
②图中有2对互补的角;③若∠BAE=90°,∠DAC=40°,则以A为顶点的所有小于平角的角的度数和为360°;④若BC=2,CD=DE=3,点F是线段BE上任意一点,则点F到点B、C、D、E的距离之和最大值为15,最小值为11,其中说法正确的个数有( )
A.1个
B.2个
C.3个
D.4个
二、填空题
13、已知线段AB=1
996
cm,P、Q是线段AB上的两个点,线段AQ=1
200
cm,线段BP=1
050
cm,
则线段PQ=___________.
14、已知线段AB=10
cm,BC=5
cm,A、B、C三点在同一条直线上,则AC=_
_.
15、如图,线段AB=BC=CD=DE=1
cm,那么图中所有线段的长度之和等于________cm.
16、如图,点O是直线AD上一点,射线OC、OE分别是∠AOB、∠BOD的平分线,若∠AOC=28°,
则∠COD=_________,∠BOE=__________.
17、如图,将一副三角板叠放在一起,使直角的顶点重合于点O,则∠AOB+∠DOC=
°
18、如图,直线AB,CD,EF交于点O,OG平分∠BOF,且CD⊥EF,∠AOE=70°,则∠DOG=________°.
19、如图,OM平分∠AOB,ON平分∠COD.若∠MON=50°,∠BOC=10°,则∠AOD=
__________.
19、35.15°=
°
′
″;12°15′36″=
°.
20、已知射线OA,从O点再引射线OB,OC,使∠AOB=67°31′,∠BOC=48°39′,
则∠AOC的度数为
21、如图,将一张长方形纸片ABCD分别沿着BE、BF折叠,使边AB、CB均落在BD上,得到折痕BE、BF,则∠ABE+∠CBF=
.
22、如图,O是直线AB上的一点,OC,OD,OE是从点O引出的三条射线,
且∠1∶∠2∶∠3∶∠4=1∶2∶3∶4,则∠5= °.?
23、如图所示,直线AB,CD,EF交于点O,OG平分∠BOF,且CD⊥EF,若∠AOE
=
70°,
则∠DOG
=
_________
.
24、如图所示,由泰山到青岛的某一次列车,运行途中停靠的车站依次是:泰山﹣济南﹣淄博﹣潍坊﹣青岛,那么要为这次列车制作的火车票有
________种.
三、解答题
25、如图,C,D是线段AB上的两点,已知M,N分别为AC,DB的中点,AB=18cm,且AC:CD:DB=1:2:3,求线段MN的长.
26、已知点C,线段AB.
(1)如图,若点C在线段AB上,且AC=12,BC=8,点M、N分别是AC、BC的中点,则线段MN的长度是
;
(2)若把(1)中点C在线段AB上,且AC=12,BC=8,改为点C是线段AB上任意一点,且AC=a,BC=b,其他条件不变,请求出线段MN的长度(用含a、b的式子表示);
(3)若把(2)中点C是线段AB上任意一点,改为点C是直线AB上任意一点,其他条件不变,则线段MN的长度会变化吗?若有变化,求出结果.
27、如图,直线AB,CD相交于点O,OE⊥OF,OC平分∠AOE,且∠BOF=2∠BOE.求∠DOB的度数.
28、如图,直线AB、CD相交于点O,OE平分∠AOD,∠FOC=90°,∠1=40°,求∠2和∠3的度数.
29、如图,射线OC的端点O在直线AB上,OE⊥OC于点O,且OE平分∠BOD,OF平分∠AOE,
若∠BOC=70°,分别求∠DOE与∠DOF的度数.
30、已知:如图,∠AOB是直角,∠AOC=40°,ON是∠AOC的平分线,OM是∠BOC的平分线.
(1)求∠MON的大小.
(2)当锐角∠AOC的大小发生改变时,∠MON的大小是否发生改变?为什么?
31、如图1,点A、O、B依次在直线MN上,现将射线OA绕点O沿顺时针方向以每秒4°的速度旋转,同时射线OB绕点O沿逆时针方向以每秒6°的速度旋转,直线MN保持不动,如图2,设旋转时间为t(0≤t≤60,单位秒)
(1)当t=3时,求∠AOB的度数;
(2)在运动过程中,当∠AOB第二次达到72°时,求t的值;
(3)在旋转过程中是否存在这样的t,使得射线OB与射线OA垂直?如果存在,请求出t的值;如果不存在,请说明理由.
32、如图1,O为直线AB上一点,过点O作射线OC,∠AOC=30°,将一直角三角尺(∠M=30°)的直角顶点放在点O处,一边ON在射线OA上,另一边OM与OC都在直线AB的上方.
(1)若将图1中的三角尺绕点O以每秒5°的速度,沿顺时针方向旋转t秒,当OM恰好平分∠BOC时,如图2.①求t值;②试说明此时ON平分∠AOC;
(2)将图1中的三角尺绕点O顺时针旋转,设∠AON=α,∠COM=β,当ON在∠AOC内部时,试求α与β的数量关系;
(3)若将图1中的三角尺绕点O以每秒5°的速度沿顺时针方向旋转的同时,射线OC也绕点O以每秒8°的速度沿顺时针方向旋转,如图3,那么经过多长时间,射线OC第一次平分∠MON?请说明理由.
2020-2021苏科版七年级数学上册第6章平面图形的认识(一)
综合
培优训练卷(1)(答案)
一、选择题
1、如图,下列不正确的几何语句是(
)
A.直线AB与直线BA是同一条直线
B.射线OA与射线OB是同一条射线
C.射线OA与射线AB是同一条射线
D.线段AB与线段BA是同一条线段
解析:射线OA与射线AB不是同一条射线,因为端点不同.故选C
2、下列语句:①一条直线有且只有一条垂线;②不相等的两个角一定不是对顶角;
③两条不相交的直线叫做平行线;
④若两个角的一对边在同一直线上,另一对边互相平行,则这两个角相等;
⑤不在同一直线上的四个点可画6条直线;
⑥如果两个角是邻补角,那么这两个角的平分线组成的图形是直角.
其中错误的有(
)
A.2个
B.3个
C.4个
D.5个
解析:①一条直线有无数条垂线,故①错误;
②不相等的两个角一定不是对顶角,故②正确;
③在同一平面内,两条不相交的直线叫做平行线,故③错误;
④若两个角的一对边在同一直线上,另一对边互相平行,则这两个角相等或互补,故④错误;
⑤不在同一直线上的四个点可画4或6条直线,故⑤错误;
⑥如果两个角是邻补角,那么这两个角的平分线组成的图形是直角,故⑥正确.
所以错误的有4个,故选C.
3、如图,B是线段AD的中点,C是BD上一点,则下列结论中错误的是(
)
A.BC=AB-CD
B.BC=AD-CD
C.BC=(AD+CD)
D.BC=AC-BD
解析:∵
B是线段AD的中点,∴
AB=BD=AD.
A.BC=BD-CD=AB-CD,故本选项正确;
B.BC=BD-CD=AD-CD,故本选项正确;
D.BC=AC-AB=AC-BD,故本选项正确.只有C选项是错误的.
4、当时钟指向上午10:10分,时针与分针的夹角是多少度( )
A.115°
B.120°
C.105°
D.90°
【解答】解:时钟指向上午10:10分,时针与分针相距3份,
时钟指向上午10:10分,时针与分针的夹角是多少度30°115°,
或时针与分针的夹角是120°﹣10×()°=115°;
故选:A.
5、一个角的补角比这个角的余角的3倍少20°,这个角的度数是( )
A.30°
B.35°
C.40°
D.45°
【解答】解:设这个角为α,则它的补角为180°﹣α,余角为90°﹣α,
根据题意得,180°﹣α=3(90°﹣α)﹣20°,
解得α=35°.
故选:B.
6、如果∠α与∠β是邻补角,且∠α>∠β,那么∠β的余角是(
)
A.(∠α+∠β)
B.∠α
C.(∠α-∠β)
D.不能确定
解析:因为∠α与∠β是邻补角,所以∠α+∠β=180°,(∠α+∠β)=90°.
所以∠β的余角是90°-∠β=(∠α+∠β)-∠β=(∠α-∠β),故选C.
7、如果∠1与∠2互补,∠2与∠3互余,则∠1与∠3的关系是(
)
A.∠1=∠3
B.∠1=180°-∠3
C.∠1=90°+∠3
D.以上都不对
解析:∵
∠1+∠2=180°,∴
∠1=180°-∠2.
又∵
∠2+∠3=90°,∴
∠3=90°-∠2.
∴
∠1-∠3=90°,即∠1=90°+∠3,故选C.
8、下列说法正确的是(
)
A.在同一平面内,不相交的两条线段平行
B.
在同一平面内,不相交的两条射线平行
C.
不相交的直线一定是平行线
D.
在同一平面内,两条直线的关系只有两种:平行或相交
答案:D
9、如图,已知ON⊥L,OM⊥L,所以OM与ON重合,其理由是(
B
)
A.两点确定一条直线
B.在同一平面内,经过一点有且只有一条直线与已知直线垂直
C.在同一平面内,过一点只能作一条垂线
D.垂线段最短
10、如图,把水渠中的水引到水池C,先过C点向渠岸AB画垂线,垂足为点D,再沿垂线CD开沟才能使沟最短,其依据是
(
)
A.垂线最短
B.过一点确定一条直线与已知直线垂直
C.垂线段最短
D.以上说法都不对
答案:C
“垂线”是直线,不可度量;“垂线段”是线段,可以度量。
11、如图,点A在直线l1上,点B,C在直线l2上,AB⊥l2,AC⊥l1,AB=4,BC=3,AC=5,有下列说法:
(1)点B到直线l1的距离等于4
(2)点C到直线l1的距离等于5
(3)点A到直线l2间的距离等于4
(4)点B到直线AC的距离等于3
其中正确的说法有(
)
A.1个
B.2个
C.3个
D.4个
答案:B
由点到直线的距离的定义可知,只有说法(2)、(3)正确
12、如图,C、D在线段BE上,下列说法:①直线CD上以B、C、D、E为端点的线段共有6条;
②图中有2对互补的角;③若∠BAE=90°,∠DAC=40°,则以A为顶点的所有小于平角的角的度数和为360°;④若BC=2,CD=DE=3,点F是线段BE上任意一点,则点F到点B、C、D、E的距离之和最大值为15,最小值为11,其中说法正确的个数有( )
A.1个
B.2个
C.3个
D.4个
【解析】①以B、C、D、E为端点的线段BC、BD、BE、CE、CD、DE共6条,故①正确;
②图中互补的角就是分别以C、D为顶点的两对邻补角,即∠BCA和∠ACD互补,∠ADE和∠ADC互补,故②正确;
③由∠BAE=90°,∠CAD=40°,根据图形可以求出
∠BAC+∠DAE+∠DAC+∠BAE+∠BAD+∠CAE=90°+90°+90°+40°=310°,故③错误;
④当F在线段CD上,则点F到点B、C、D、E的距离之和最小为FB+FE+FD+FC=11,当F和E重合,则点F到点B、C、D、E的距离之和最大为FB+FE+FD+FC=8+0+6+3=17,故④错误.
故选B.
二、填空题
13、已知线段AB=1
996
cm,P、Q是线段AB上的两个点,线段AQ=1
200
cm,线段BP=1
050
cm,
则线段PQ=___________.
解析:如图,由题意得:AQ+BP=AB+PQ=1
200+1
050=2
250(cm),
∴
PQ=2
250-1
996=254(cm).
14、已知线段AB=10
cm,BC=5
cm,A、B、C三点在同一条直线上,则AC=_
_.
解析:本题有两种情形:
(1)当点C在线段AB上时,如图,有AC=AB-BC,
又∵
AB=10
cm,BC=5
cm,∴
AC=10-5=5(cm);
(2)当点C在线段AB的延长线上时,如图,有AC=AB+BC,
又∵
AB=10
cm,BC=5
cm,∴
AC=10+5=15(cm).
故线段AC=5
cm或15
cm.
15、如图,线段AB=BC=CD=DE=1
cm,那么图中所有线段的长度之和等于________cm.
解析:因为长为1
cm的线段共4条,长为2
cm的线段共3条,长为3
cm的线段共2条,长为4
cm的线段仅1条,
所以图中所有线段长度之和为1×4+2×3+3×2+4×1=20(cm).
16、如图,点O是直线AD上一点,射线OC、OE分别是∠AOB、∠BOD的平分线,若∠AOC=28°,
则∠COD=_________,∠BOE=__________.
解析:∵
∠AOC+∠COD=180°,∠AOC=28°,∴
∠COD=152°.
∵
OC是∠AOB的平分线,∠AOC=28°,∴
∠AOB=2∠AOC=2×28°=56°,
∴
∠BOD=180°-∠AOB=180°-56°=124°.
∵
OE是∠BOD的平分线,∴
∠BOE=∠BOD=×124°=62°.
17、如图,将一副三角板叠放在一起,使直角的顶点重合于点O,则∠AOB+∠DOC=
180
°
18、如图,直线AB,CD,EF交于点O,OG平分∠BOF,且CD⊥EF,∠AOE=70°,则∠DOG=________°.
答案:因为∠BOF=∠AOE=70°,所以∠BOG==35°,所以∠DOG=∠BOD+∠BOG=55°。
19、如图,OM平分∠AOB,ON平分∠COD.若∠MON=50°,∠BOC=10°,则∠AOD=
__________.
解析:∵
OM平分∠AOB,ON平分∠COD,
∴
∠AOM=∠BOM,∠CON=∠DON.
∵
∠MON=50°,∠BOC=10°,
∴
∠MON-∠BOC
=40°,即∠BOM+∠CON=40°.
∴
∠AOD=∠MON+∠AOM+∠DON=∠MON+∠BOM+∠CON=50°+40°=90°.
19、35.15°=
°
′
″;12°15′36″=
°.
【解答】解:∵0.15°=9′,∴35.15°=35°9′;
∵36″=0.6′,15.6′=0.26°,∴12°15′36″=12.26°,
故答案为:35,9,0;12.26.
20、已知射线OA,从O点再引射线OB,OC,使∠AOB=67°31′,∠BOC=48°39′,
则∠AOC的度数为
【解析】如右图所示,
①OC在OA、OB之间,∵∠AOB=67°31′,∠BOC=48°39′,
∴∠AOC=∠AOB﹣∠BOC=67°31′﹣48°39′=66°91′﹣48°39′=18°52′;
②OB在OA、OC之间,
∵∠AOB=67°31′,∠BOC=48°39′,
∴∠AOC=∠AOB+∠BOC=67°31′+48°39′=115°70′=116°10′;
故答案是18°52′或116°10′.
21、如图,将一张长方形纸片ABCD分别沿着BE、BF折叠,使边AB、CB均落在BD上,得到折痕BE、BF,则∠ABE+∠CBF=
.
【解析】由折叠得,∠ABE=∠DBE,∠CBF=∠DBF,
∵∠ABE+∠DBE+∠CBF+∠DBF=∠ABC=90°,
∴∠ABE+∠CBF=∠ABC=×90°=45°,
故答案为45°.
22、如图,O是直线AB上的一点,OC,OD,OE是从点O引出的三条射线,
且∠1∶∠2∶∠3∶∠4=1∶2∶3∶4,则∠5= °.?
[解析]
设∠1=x°,则∠2=2x°,∠3=3x°.依题意,得x+2x+3x=180,解得x=30,
所以∠4=4x°=120°,∠5=180°-120°=60°.
23、如图所示,直线AB,CD,EF交于点O,OG平分∠BOF,且CD⊥EF,若∠AOE
=
70°,
则∠DOG
=
____55_____
.
24、如图所示,由泰山到青岛的某一次列车,运行途中停靠的车站依次是:泰山﹣济南﹣淄博﹣潍坊﹣青岛,那么要为这次列车制作的火车票有
________种.
【解析】解:如图,设泰山﹣﹣济南﹣﹣淄博﹣﹣潍坊﹣﹣青岛五站分别用A、B、C、D、E表示,
则共有线段:AB、AC、AD、AE、BC、BD、BE、CD、CE、DE共10条,
所以,需要制作火车票10×2=20种.
故答案为:20.
三、解答题
25、如图,C,D是线段AB上的两点,已知M,N分别为AC,DB的中点,AB=18cm,且AC:CD:DB=1:2:3,求线段MN的长.
【解答】解:设AC,CD,DB的长分别为xcm,2xcm,3xcm
∵AC+CD+DB=AB,AB=18cm,
∴x+2x+3x=18,
解得x=3
∴AC=3cm,CD=6cm,DB=9cm
∵M,N为AC,DB的中点,
∴
∴MN=MC+CD+DN=12cm,
∴MN的长为12cm.
26、已知点C,线段AB.
(1)如图,若点C在线段AB上,且AC=12,BC=8,点M、N分别是AC、BC的中点,则线段MN的长度是
;
(2)若把(1)中点C在线段AB上,且AC=12,BC=8,改为点C是线段AB上任意一点,且AC=a,BC=b,其他条件不变,请求出线段MN的长度(用含a、b的式子表示);
(3)若把(2)中点C是线段AB上任意一点,改为点C是直线AB上任意一点,其他条件不变,则线段MN的长度会变化吗?若有变化,求出结果.
【解答】解:(1)点M、N分别是AC、BC的中点,AC=12,BC=8,
MC=AC÷2=12÷2=6,
NC=CB÷2=8÷2=4,
由线段的和差,得MN=MC+NC=6+4=10.
答:线段MN的长是10,
故答案为:10;
(2)由点M、N分别是AC、BC的中点,可得,
所以
(3)线段MN的长度会变化
当点C在线段AB上时,由(2)知
当点C在线段AB上的延长线时,如图,
则AC>BC,即a>b.
由点M、N分别是AC、BC的中点.
可得,.
所以.
当点C在线段BA上的延长线时,如图.
则BC>AC,即b>a.
由点M、N分别是AC、BC的中点.可得,.
所以.
27、如图,直线AB,CD相交于点O,OE⊥OF,OC平分∠AOE,且∠BOF=2∠BOE.求∠DOB的度数.
解:因为OE⊥OF,所以∠EOF=90°.
因为∠BOF=2∠BOE,所以3∠BOE=90°,即∠BOE=30°,所以∠AOE=180°-∠BOE=150°.
因为OC平分∠AOE,所以∠AOC=∠AOE=75°,所以∠DOB=∠AOC=75°.
28、如图,直线AB、CD相交于点O,OE平分∠AOD,∠FOC=90°,∠1=40°,求∠2和∠3的度数.
解:∵
∠FOC=90°,∠1=40°,AB为直线,
∴
∠3+∠FOC+∠1=180°,
∴
∠3=180°-90°-40°=50°.
∵
∠3与∠AOD互补,∴
∠AOD=180°-∠3=130°.
∵
OE平分∠AOD,
∴
∠2=∠AOD=65°.
29、如图,射线OC的端点O在直线AB上,OE⊥OC于点O,且OE平分∠BOD,OF平分∠AOE,
若∠BOC=70°,分别求∠DOE与∠DOF的度数.
【解答】解:∵OE⊥OC于点O,∴∠COE=90°,
∵∠BOC=70°,∴∠BOE=∠COE﹣∠BOC=90°﹣70°=20°,
∵OE平分∠BOD,∴∠DOE=∠BOE=20°,
∵∠AOB=180°,∴∠AOE=180°﹣∠BOE=180°﹣20°=160°,
∵OF平分∠AOE,∴∠EOF∠AOE=80°,∴∠DOF=∠EOF﹣∠DOE=80°﹣20°=60°,
综上,∠DOE的度数为20°,∠DOF的度数为60°.
30、已知:如图,∠AOB是直角,∠AOC=40°,ON是∠AOC的平分线,OM是∠BOC的平分线.
(1)求∠MON的大小.
(2)当锐角∠AOC的大小发生改变时,∠MON的大小是否发生改变?为什么?
解:(1)∵
∠AOB是直角,∠AOC=40°,∴
∠AOB+∠AOC=90°+40°=130°.
∵
OM是∠BOC的平分线,ON是∠AOC的平分线,
∴
∠MOC=∠BOC=65°,∠NOC=∠AOC=20°.
∴
∠MON=∠MOC-∠NOC=65°-20°=45°.
(2)当锐角∠AOC的大小发生改变时,∠MON的大小不发生改变.
∵
∠MON=∠MOC-∠NOC=∠BOC-∠AOC=(∠BOC-∠AOC)=∠AOB,
又∠AOB=90°,∴
∠MON=∠AOB=45°.
31、如图1,点A、O、B依次在直线MN上,现将射线OA绕点O沿顺时针方向以每秒4°的速度旋转,同时射线OB绕点O沿逆时针方向以每秒6°的速度旋转,直线MN保持不动,如图2,设旋转时间为t(0≤t≤60,单位秒)
(1)当t=3时,求∠AOB的度数;
(2)在运动过程中,当∠AOB第二次达到72°时,求t的值;
(3)在旋转过程中是否存在这样的t,使得射线OB与射线OA垂直?如果存在,请求出t的值;如果不存在,请说明理由.
【解答】解:(1)当t=3时,∠AOB=180°﹣4°×3﹣6°×3=150°.
(2)依题意,得:4t+6t=180+72,解得:t.
答:当∠AOB第二次达到72°时,t的值为.
(3)当0≤t≤18时,180﹣4t﹣6t=90,解得:t=9;
当18≤t≤60时,4t+6t=180+90或4t+6t=180+270,解得:t=27或t=45.
答:在旋转过程中存在这样的t,使得射线OB与射线OA垂直,t的值为9、27或45.
32、如图1,O为直线AB上一点,过点O作射线OC,∠AOC=30°,将一直角三角尺(∠M=30°)的直角顶点放在点O处,一边ON在射线OA上,另一边OM与OC都在直线AB的上方.
(1)若将图1中的三角尺绕点O以每秒5°的速度,沿顺时针方向旋转t秒,当OM恰好平分∠BOC时,如图2.①求t值;②试说明此时ON平分∠AOC;
(2)将图1中的三角尺绕点O顺时针旋转,设∠AON=α,∠COM=β,当ON在∠AOC内部时,试求α与β的数量关系;
(3)若将图1中的三角尺绕点O以每秒5°的速度沿顺时针方向旋转的同时,射线OC也绕点O以每秒8°的速度沿顺时针方向旋转,如图3,那么经过多长时间,射线OC第一次平分∠MON?请说明理由.
【解答】解:(1)①如图2中,∵∠AOC=30°,∴∠BOC=180°﹣∠AOC=150°,
∵OM平分∠BOC,∴∠COM=∠BOM∠BOC=75°,∠AON=180°﹣90°﹣75°=15°,
∴t3s,
②当t=3时,∠AON=3t=15°,∠CON=30°﹣3t=15°,∴∠AON=∠CON,
∴ON平分∠AOC;
(2)∵∠CON=30°﹣α=90°﹣β,∴β=α+60°;
(3)∵OC平分∠MON,∠MON=90°,∴∠CON=∠COM=45°,
∵三角板绕点O以每秒5°的速度,射线OC也绕O点以每秒8°的速度沿顺时针方向旋转一周,
∴设∠AON=5t,∠AOC=30+8t,
∵∠AOC﹣∠AON=∠CON,∴30+8t﹣5t=45,解得t=5,
∴经过5秒OC平分∠MON.
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
