初二【数学(北京版)】11.7二次根式的加减法(3) 教学设计
文档属性
| 名称 | 初二【数学(北京版)】11.7二次根式的加减法(3) 教学设计 |
|
|
| 格式 | zip | ||
| 文件大小 | 221.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-04 00:00:00 | ||
图片预览


文档简介
课程基本信息
课题
二次根式加减法(3)
教科书
书名:义务教育教科书
出版社:北京出版社
出版日期:
2014
年
7
月
教学目标
教学目标:1.灵活运用二次根式性质、运算法则和运算律,解决二次根式混合运算的计算问题;2.类比整式运算探讨二次根式的混合运算,体会类比思想在学习新知中的作用;3.细致观察算式结构,合理选择运算顺序.教学重点:类比整式运算探讨二次根式的混合运算.教学难点:准确观察算式结构,正确使用运算律和运算性质,选择合理的运算顺序.
教学过程
时间
教学环节
主要师生活动
复习引入例题讲解巩固练习课堂小结课后练习
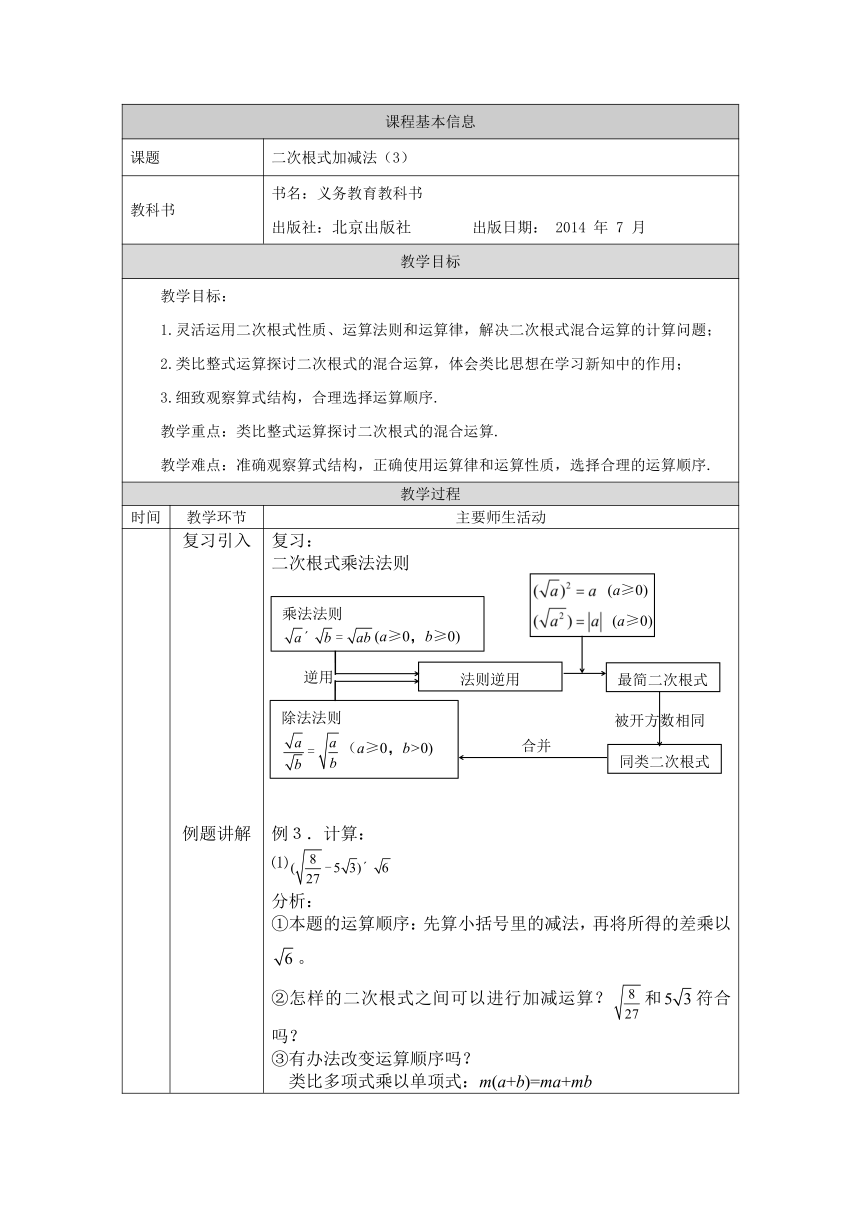
复习:二次根式乘法法则例3.计算:⑴
分析:①本题的运算顺序:先算小括号里的减法,再将所得的差乘以。②怎样的二次根式之间可以进行加减运算?和符合吗?③有办法改变运算顺序吗?类比多项式乘以单项式:m(a+b)=ma+mb
解:
先化简为最简二次根式=
再运算
=
逆用
=
凑出
=解法二:
步骤:=
1.多项式乘单项式法则=
2.二次根式乘法法则=
3.二次根式加法则,系数使用假分数。=
⑵类比多项式乘以多项式:(a+b)(m+n)=am+an+bm+bn解:
=
=
=小结:你在计算的过程中使用了哪些运算法则或性质?
你愿意先化成最简二次根式再相乘,还是先相乘再化简?你觉得自己选取的顺序有什么优势?例4.计算:⑴
分析:可类比多项式乘多项式法则进行运算。分析:观察算式,符合平方差公式(a+b)(a-b)=a2-b2,相当于公式里的a,相当于公式里的b。解:
=
=
=-6变式:
辨结构,解:
抓特殊,
=
巧变形,
=
利运算.
=
=
=6⑵分析:观察算式,符合完全平方公式(a-b)2=a2-2ab+b2,相当于公式里的a,相当于公式里的b。解:
=
=
=练习⑴⑵⑶小结:1.观察算式特征,明确运算顺序。2.除二次根式自身的性质及运算法则外,在实数和整式中学过的运算律和运算性质,在二次根式的运算中都可以应用。3.结果中如果含有二次根式,要化为最简二次根式。4.灵活利用性质和运算法则,无论是二次根式的运算还是化简,每一步都要有依据。5.在解决二次根式运算时,类比整式运算.类比的方法在探究新问题经常用到。计算:⑴;⑵;⑶
;⑷.
合并
逆用
除法法则
(a≥0,b>0)
法则逆用
(a≥0)
(a≥0)
最简二次根式
同类二次根式
被开方数相同
乘法法则
(a≥0,b≥0)
课题
二次根式加减法(3)
教科书
书名:义务教育教科书
出版社:北京出版社
出版日期:
2014
年
7
月
教学目标
教学目标:1.灵活运用二次根式性质、运算法则和运算律,解决二次根式混合运算的计算问题;2.类比整式运算探讨二次根式的混合运算,体会类比思想在学习新知中的作用;3.细致观察算式结构,合理选择运算顺序.教学重点:类比整式运算探讨二次根式的混合运算.教学难点:准确观察算式结构,正确使用运算律和运算性质,选择合理的运算顺序.
教学过程
时间
教学环节
主要师生活动
复习引入例题讲解巩固练习课堂小结课后练习
复习:二次根式乘法法则例3.计算:⑴
分析:①本题的运算顺序:先算小括号里的减法,再将所得的差乘以。②怎样的二次根式之间可以进行加减运算?和符合吗?③有办法改变运算顺序吗?类比多项式乘以单项式:m(a+b)=ma+mb
解:
先化简为最简二次根式=
再运算
=
逆用
=
凑出
=解法二:
步骤:=
1.多项式乘单项式法则=
2.二次根式乘法法则=
3.二次根式加法则,系数使用假分数。=
⑵类比多项式乘以多项式:(a+b)(m+n)=am+an+bm+bn解:
=
=
=小结:你在计算的过程中使用了哪些运算法则或性质?
你愿意先化成最简二次根式再相乘,还是先相乘再化简?你觉得自己选取的顺序有什么优势?例4.计算:⑴
分析:可类比多项式乘多项式法则进行运算。分析:观察算式,符合平方差公式(a+b)(a-b)=a2-b2,相当于公式里的a,相当于公式里的b。解:
=
=
=-6变式:
辨结构,解:
抓特殊,
=
巧变形,
=
利运算.
=
=
=6⑵分析:观察算式,符合完全平方公式(a-b)2=a2-2ab+b2,相当于公式里的a,相当于公式里的b。解:
=
=
=练习⑴⑵⑶小结:1.观察算式特征,明确运算顺序。2.除二次根式自身的性质及运算法则外,在实数和整式中学过的运算律和运算性质,在二次根式的运算中都可以应用。3.结果中如果含有二次根式,要化为最简二次根式。4.灵活利用性质和运算法则,无论是二次根式的运算还是化简,每一步都要有依据。5.在解决二次根式运算时,类比整式运算.类比的方法在探究新问题经常用到。计算:⑴;⑵;⑶
;⑷.
合并
逆用
除法法则
(a≥0,b>0)
法则逆用
(a≥0)
(a≥0)
最简二次根式
同类二次根式
被开方数相同
乘法法则
(a≥0,b≥0)
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
