京改版八年级上册12.11勾股定理(1) 教学设计
文档属性
| 名称 | 京改版八年级上册12.11勾股定理(1) 教学设计 |

|
|
| 格式 | zip | ||
| 文件大小 | 248.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-03 00:00:00 | ||
图片预览



文档简介
课程基本信息
课题
勾股定理
教科书
书名:
数学
出版社:北京出版社
出版日期:
2014
年
7
月
教学目标
教学目标:经历勾股定理的探索过程,了解勾股定理的各种探究方法及内在联系,进一步发展学生的空间观念和推理能力。
教学重点:探索、验证勾股定理.
教学难点:勾股定理的证明.
教学过程
时间
教学环节
主要师生活动
2′
13′
8′
2′
复习回顾
实践探究
实践探究
实践探究
实践探究
实践探究
新知应用
新知应用
新知应用
课堂总结
环节一:复习回顾
1、什么是直角三角形?
有一个角是直角的三角形叫做直角三角形.
2、三角形的主要元素是边和角,三角形的边之间有什么关系?三角形的角之间有什么关系?
前面,我们学习过三角形两边之和大于第三边,两边之差小于第三边。
3、直角三角形的角之间有什么特殊关系?直角三角形的两锐角互余.
4、对于直角三角形,三条边的长度之间有什么样确定的数量关系吗?
环节二:实践探究
1、在无理数的学习中,我们认识了
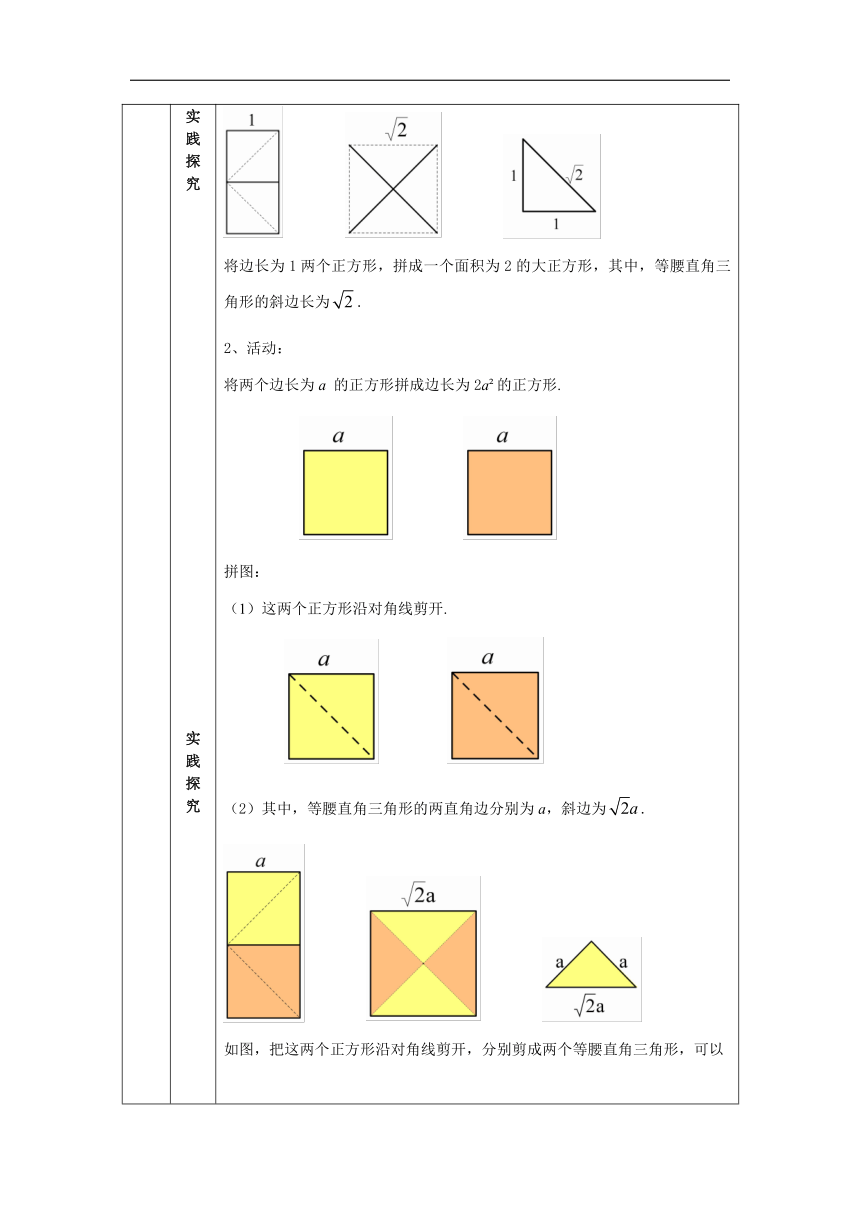
将边长为1两个正方形,拼成一个面积为2的大正方形,其中,等腰直角三角形的斜边长为.
2、活动:
将两个边长为a
的正方形拼成边长为2a?的正方形.
拼图:
(1)这两个正方形沿对角线剪开.
(2)其中,等腰直角三角形的两直角边分别为a,斜边为.
如图,把这两个正方形沿对角线剪开,分别剪成两个等腰直角三角形,可以拼成一个面积为2a?的大正方形,此时,拼成的大正方形边长为.
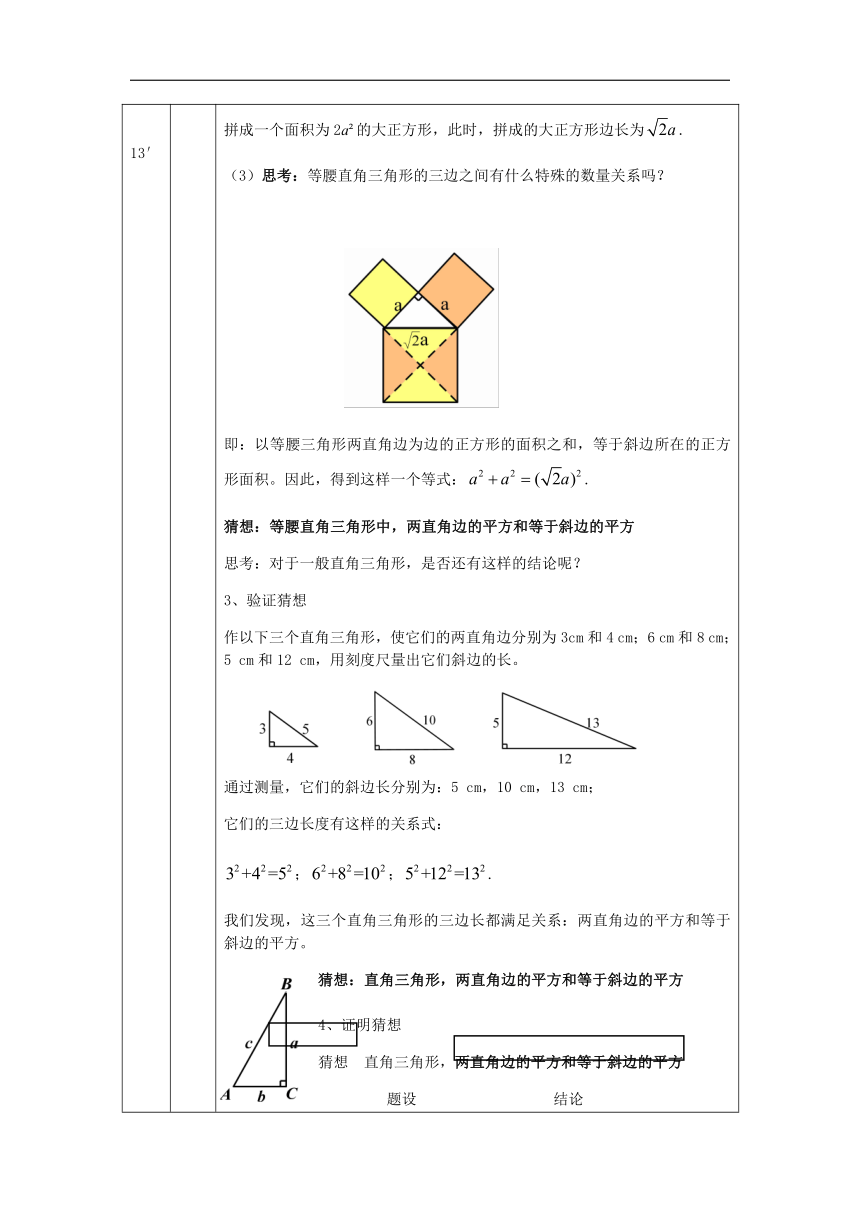
(3)思考:等腰直角三角形的三边之间有什么特殊的数量关系吗?
即:以等腰三角形两直角边为边的正方形的面积之和,等于斜边所在的正方形面积。因此,得到这样一个等式:.
猜想:等腰直角三角形中,两直角边的平方和等于斜边的平方
思考:对于一般直角三角形,是否还有这样的结论呢?
3、验证猜想
作以下三个直角三角形,使它们的两直角边分别为3cm和4
cm;6
cm和8
cm;5
cm和12
cm,用刻度尺量出它们斜边的长。
通过测量,它们的斜边长分别为:5
cm,10
cm,13
cm;
它们的三边长度有这样的关系式:
;;.
我们发现,这三个直角三角形的三边长都满足关系:两直角边的平方和等于斜边的平方。
猜想:直角三角形,两直角边的平方和等于斜边的平方
4、证明猜想
猜想
直角三角形,两直角边的平方和等于斜边的平方
题设
结论
已知:Rt△ABC中,∠C=90°,a,b,c分别
是∠A,∠B,∠C的对边.
求证:a2
+
b2
=
c2.
数
形
完全平方公式
正方形面积
(a
+
b)
2
=
a2+2ab+
b2
a2,
b2,
c2
矩形面积
或直角三角形面积
(1)动手操作
拼一拼
请同学们拿出四个全等的直角三角形(设较短的直角边为a,较长的直角边为b,斜边为c),拼一个正方形.
证法一:
在边长为C的大正方形外,拼接四个边长为a,b的直角三角形,由于直角三角形两锐角互余,所以,可以拼成一个边长为a+b的大正方形,通过大正方形的面积与四个直角三角形和边长为c的小正方形面积之和相等,可得
证明:∵
(a
+
b)
2
=
c2
+
∴
a
2
+
2
ab
+
b2
=
c2
+
2
ab
∴
a
2
+
b2
=
c2
证法二:
证明:∵
∴
a
2
+
b2
=
c2
从形和数两个角度证明了a
2
+
b2
=
c2
得出定理:
勾股定理
直角三角形,两直角边的平方和等于第三边平方.(文字语言)
(图形语言)
(符号语言)
在△ABC中,
∵∠C=90°,
∴a
2
+
b2
=
c2(勾股定理)
勾股史话:我国早在三千多年就知道了这个定理,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”,我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.因此就把这一定理称为勾股定理.
勾
股
注意:勾股定理前提条件是直角三角形,要明确直角,进而确定斜边.
∵∠C=90°,∴c是斜边
∴a
2
+
b2
=
c2
∵∠B=90°,∴b是斜边
∴a
2
+
c
2
=
b
2
∵∠A=90°,∴a是斜边
∴c
2
+
b2
=
a
2
所以,应用勾股定理时,一定要先确定斜边.
环节三:新知应用
例
在
Rt△ABC
中,∠C=90°,∠A,∠B,∠C的对边
分别为a,b,c.如果
a=5,b=3,求c.
解:在
Rt
△
ABC
中,
∠C=90°,
∴a
2
+
b2
=
c2,(勾股定理).
∵
a=5,b=3,
∴
.
∴
c=
也可以用直接计算
变式
在
Rt
△
ABC
中,已知∠C=90°,∠A,∠B,∠C的对边分别为a,b
,c.如果a=5,c=6,求b.
解:在
Rt
△
ABC
中,
∠C=90°,
∴a
2
+
b2
=
c2,(勾股定理).
∵a=5,c=6,
∴
∴b=.
也可以用直接计算.
如果已知b,c,也可以直接用计算.
例
一颗大树被大风刮倒,断的一段恰好落在地面上的A处,量得BC=5m,AC=10m,试计算大树的高度(结果精确到1m)
转化
实际问题————数学问题
已知:如图,在
Rt
△
ABC
中,∠C=90°,BC=5m,AC=10m.
求:AB
+
BC
的长.
解:在Rt△ABC中,∵∠C=90°,BC=5m,AC=10m.
∴BC
?
+
AC
?
=
AB
?(勾股定理).
∴AB
?
=
5?
+
10?
=
125.
∴AB
=
(m)
.
∴AB
+
BC
=5+(m)
.
实际问题的解:
∵AB
=≈
11(m)
.
∴AB
+
BC
≈
16(m)
.
树高=AB
+
BC
≈
16(m)
.
答:大树高约16m.
环节四:课堂总结
本节课学习了什么知识?
勾股定理:直角三角形中,两条直角边的平方和等于斜边的平方.
a
2
+
b2
=
c2,
也可以利用以下几种变形,直接计算:
学习勾股定理时,我们用了研究哪些方法?
观察—实验—猜想—证明
如何探究勾股定理,经历了哪些过程?
从特殊到一般,探究和猜想勾股定理
思想方法的小结:数形结合的方法.
直角三角形的性质:角——直角三角形中,两锐角互余;边——直角三角形中,两直角边的平方和等于斜边的平方(勾股定理).
作业:
1.
在
Rt
△
ABC
中,已知∠C=90°,∠A,
∠B,
∠C的对边
分别为a,b
,c.如果
a=9,b=12
,求c.
2.
已知:如图,∠C=∠D=90°,AC=8,BC=6,AD=7.
求BD的长.
课题
勾股定理
教科书
书名:
数学
出版社:北京出版社
出版日期:
2014
年
7
月
教学目标
教学目标:经历勾股定理的探索过程,了解勾股定理的各种探究方法及内在联系,进一步发展学生的空间观念和推理能力。
教学重点:探索、验证勾股定理.
教学难点:勾股定理的证明.
教学过程
时间
教学环节
主要师生活动
2′
13′
8′
2′
复习回顾
实践探究
实践探究
实践探究
实践探究
实践探究
新知应用
新知应用
新知应用
课堂总结
环节一:复习回顾
1、什么是直角三角形?
有一个角是直角的三角形叫做直角三角形.
2、三角形的主要元素是边和角,三角形的边之间有什么关系?三角形的角之间有什么关系?
前面,我们学习过三角形两边之和大于第三边,两边之差小于第三边。
3、直角三角形的角之间有什么特殊关系?直角三角形的两锐角互余.
4、对于直角三角形,三条边的长度之间有什么样确定的数量关系吗?
环节二:实践探究
1、在无理数的学习中,我们认识了
将边长为1两个正方形,拼成一个面积为2的大正方形,其中,等腰直角三角形的斜边长为.
2、活动:
将两个边长为a
的正方形拼成边长为2a?的正方形.
拼图:
(1)这两个正方形沿对角线剪开.
(2)其中,等腰直角三角形的两直角边分别为a,斜边为.
如图,把这两个正方形沿对角线剪开,分别剪成两个等腰直角三角形,可以拼成一个面积为2a?的大正方形,此时,拼成的大正方形边长为.
(3)思考:等腰直角三角形的三边之间有什么特殊的数量关系吗?
即:以等腰三角形两直角边为边的正方形的面积之和,等于斜边所在的正方形面积。因此,得到这样一个等式:.
猜想:等腰直角三角形中,两直角边的平方和等于斜边的平方
思考:对于一般直角三角形,是否还有这样的结论呢?
3、验证猜想
作以下三个直角三角形,使它们的两直角边分别为3cm和4
cm;6
cm和8
cm;5
cm和12
cm,用刻度尺量出它们斜边的长。
通过测量,它们的斜边长分别为:5
cm,10
cm,13
cm;
它们的三边长度有这样的关系式:
;;.
我们发现,这三个直角三角形的三边长都满足关系:两直角边的平方和等于斜边的平方。
猜想:直角三角形,两直角边的平方和等于斜边的平方
4、证明猜想
猜想
直角三角形,两直角边的平方和等于斜边的平方
题设
结论
已知:Rt△ABC中,∠C=90°,a,b,c分别
是∠A,∠B,∠C的对边.
求证:a2
+
b2
=
c2.
数
形
完全平方公式
正方形面积
(a
+
b)
2
=
a2+2ab+
b2
a2,
b2,
c2
矩形面积
或直角三角形面积
(1)动手操作
拼一拼
请同学们拿出四个全等的直角三角形(设较短的直角边为a,较长的直角边为b,斜边为c),拼一个正方形.
证法一:
在边长为C的大正方形外,拼接四个边长为a,b的直角三角形,由于直角三角形两锐角互余,所以,可以拼成一个边长为a+b的大正方形,通过大正方形的面积与四个直角三角形和边长为c的小正方形面积之和相等,可得
证明:∵
(a
+
b)
2
=
c2
+
∴
a
2
+
2
ab
+
b2
=
c2
+
2
ab
∴
a
2
+
b2
=
c2
证法二:
证明:∵
∴
a
2
+
b2
=
c2
从形和数两个角度证明了a
2
+
b2
=
c2
得出定理:
勾股定理
直角三角形,两直角边的平方和等于第三边平方.(文字语言)
(图形语言)
(符号语言)
在△ABC中,
∵∠C=90°,
∴a
2
+
b2
=
c2(勾股定理)
勾股史话:我国早在三千多年就知道了这个定理,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”,我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.因此就把这一定理称为勾股定理.
勾
股
注意:勾股定理前提条件是直角三角形,要明确直角,进而确定斜边.
∵∠C=90°,∴c是斜边
∴a
2
+
b2
=
c2
∵∠B=90°,∴b是斜边
∴a
2
+
c
2
=
b
2
∵∠A=90°,∴a是斜边
∴c
2
+
b2
=
a
2
所以,应用勾股定理时,一定要先确定斜边.
环节三:新知应用
例
在
Rt△ABC
中,∠C=90°,∠A,∠B,∠C的对边
分别为a,b,c.如果
a=5,b=3,求c.
解:在
Rt
△
ABC
中,
∠C=90°,
∴a
2
+
b2
=
c2,(勾股定理).
∵
a=5,b=3,
∴
.
∴
c=
也可以用直接计算
变式
在
Rt
△
ABC
中,已知∠C=90°,∠A,∠B,∠C的对边分别为a,b
,c.如果a=5,c=6,求b.
解:在
Rt
△
ABC
中,
∠C=90°,
∴a
2
+
b2
=
c2,(勾股定理).
∵a=5,c=6,
∴
∴b=.
也可以用直接计算.
如果已知b,c,也可以直接用计算.
例
一颗大树被大风刮倒,断的一段恰好落在地面上的A处,量得BC=5m,AC=10m,试计算大树的高度(结果精确到1m)
转化
实际问题————数学问题
已知:如图,在
Rt
△
ABC
中,∠C=90°,BC=5m,AC=10m.
求:AB
+
BC
的长.
解:在Rt△ABC中,∵∠C=90°,BC=5m,AC=10m.
∴BC
?
+
AC
?
=
AB
?(勾股定理).
∴AB
?
=
5?
+
10?
=
125.
∴AB
=
(m)
.
∴AB
+
BC
=5+(m)
.
实际问题的解:
∵AB
=≈
11(m)
.
∴AB
+
BC
≈
16(m)
.
树高=AB
+
BC
≈
16(m)
.
答:大树高约16m.
环节四:课堂总结
本节课学习了什么知识?
勾股定理:直角三角形中,两条直角边的平方和等于斜边的平方.
a
2
+
b2
=
c2,
也可以利用以下几种变形,直接计算:
学习勾股定理时,我们用了研究哪些方法?
观察—实验—猜想—证明
如何探究勾股定理,经历了哪些过程?
从特殊到一般,探究和猜想勾股定理
思想方法的小结:数形结合的方法.
直角三角形的性质:角——直角三角形中,两锐角互余;边——直角三角形中,两直角边的平方和等于斜边的平方(勾股定理).
作业:
1.
在
Rt
△
ABC
中,已知∠C=90°,∠A,
∠B,
∠C的对边
分别为a,b
,c.如果
a=9,b=12
,求c.
2.
已知:如图,∠C=∠D=90°,AC=8,BC=6,AD=7.
求BD的长.
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
