京改版八年级上册13.2随机事件发生的可能性(1) 教学设计
文档属性
| 名称 | 京改版八年级上册13.2随机事件发生的可能性(1) 教学设计 |
|
|
| 格式 | zip | ||
| 文件大小 | 562.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-03 21:54:46 | ||
图片预览



文档简介
课程基本信息
课题
随机事件发生的可能性(1)
教科书
书名:
数学(八年级上)
出版社:
北京出版社
出版日期:
2015
年
1
月
教学目标
教学目标:经历转盘实验和抛掷实验的分析探究的过程,在此过程中体会随机事件发生的可能性的大小的,也可能相等;会根据事件所包含的所有可能的结果的个数比较简单事件发生可能性的大小.通过实验和问题解决,感受生活中的可能性,认识到随机事件的发生与个人愿望无关,学会用必然和偶然的观点看待我们的生活.
教学重点:认识随机事件发生可能性是有大小之分、有相等之时
教学难点:比较随机事件发生的可能性大小
教学过程
时间
教学环节
主要师生活动
一、
复习回顾
同学们好,在上节课我们一起探究了一个典型实验--摸球实验,在实验过程中我们经历了动手操作、统计数据、分析结果的过程,通过对实验结果的分析我们知道球的多少与摸到的机会的大小有关系,而摸到机会的大小也即可能性的大小,随机事件发生的可能性是有大小的,是可以比较的.在比较时我们首先需要确认每个结果发生的可能性是相等的,然后可以比较所求事件包含的结果的个数,从而比较出随机事件发生的可能性的大小.
实验探究
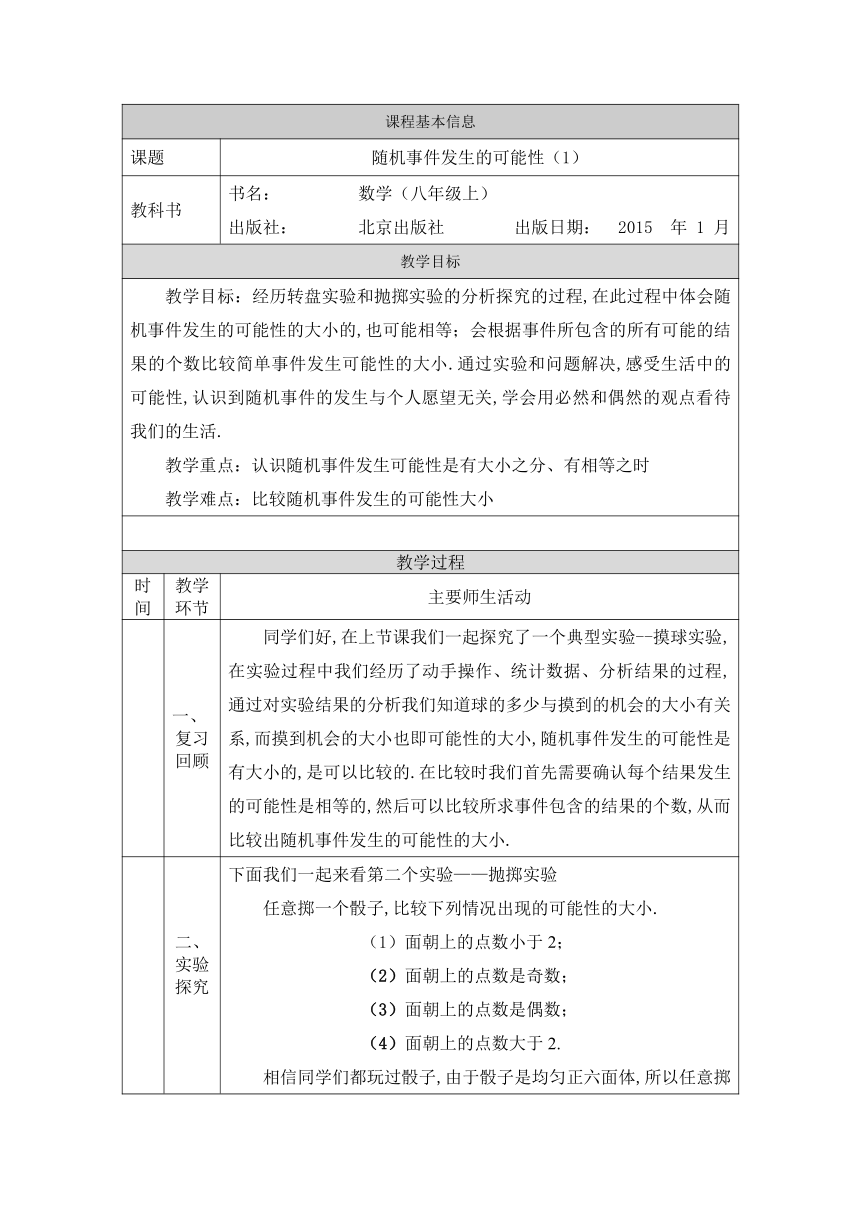
下面我们一起来看第二个实验——抛掷实验
任意掷一个骰子,比较下列情况出现的可能性的大小.
面朝上的点数小于2;
面朝上的点数是奇数;
面朝上的点数是偶数;
面朝上的点数大于2.
相信同学们都玩过骰子,由于骰子是均匀正六面体,所以任意掷一枚骰子,每个面都有机会朝上且机会相等,6个面的点数分别是:“1点”,“2点”,“3点”,“4点”,“5点”,“6点”.因此,只需比较这些点数所在的面的数量的多少就可以比较出这些面出现的可能性的大小.
解析:因为“点数小于2”的面数只有1个,即1点.“点数是奇数”
和“点数是偶数”
的面数各有3个:1点、3点、5点和2点、4点、6点.“点数大于2”的面数有4个:3点、4点、5点、6点.所以“点数小于2”出现的可能性小于“点数是奇数”
和“点数是偶数”
出现的可能性,更小于“点数大于2”出现的可能性.其中,“点数是奇数”
和“点数是偶数”
出现的可能性相等.
下面我们来看第三个实验——转盘实验
如图是一个可以转动的转盘.盘面上有8个全等的扇形区域.其中1个是红色的,2个是白色,3个是黄色,2个是绿色.用力转动转盘,当转盘停止后:
.指针对准哪种颜色区域的可能性最小?对准哪种颜色区域的可能性最大?
.指针对准白色区域与对准绿色区域的可能性有什么关系?
分析:“全等的扇形区域”
说明指针对准每个区域的机会相等,而不是对准每种颜色的机会相等,如果区域不全等,那么指针对准每个区域的机会就不等,显然对准面积大的区域机会多,可能性大.
用力转动转盘,转盘停止后,指针对准每个区域都有相等的机会,只需比较各种颜色区域数量的多少.
.因为红色区域数量最少(1个),而黄色区域数量最多(3个),所以,指针对准红色区域的可能性最小,而对准黄色区域的可能性最大.
.由于白色区域和绿色区域的数量相等(都是2个),因此,指针对准这两种颜色区域的可能性也相等.
实验小结:
到此,我们就完成了三个典型实验,第一个实验是摸球实验,第二个实验是抛掷实验,第三个实验是转盘实验.
一般的,我们把摸出某一个球,指针对准某一个区域,骰子的某一个面朝上叫做事件发生的某一个可能的结果.而摸出每个球的可能性相等.指针对准每一个区域的可能性相等,每个面朝上的可能性均等,我们又习惯的说成每个结果发生的可能性相等.当我们确认每个结果发生的可能性相等时,我们就可以比较了.
那么在第一个实验中,我们是通过比较球的数量从而比较出了摸出白球的所有可能的结果与摸出黄球的所有可能的结果的个数,从而比较出了可能性的大小.
在第二个实验中,有红扇面1个,2个是白扇面,3个黄扇面,2个绿扇面,我们通过比较不同颜色扇面的数量又比较出了什么呢?比较出了指向黄色区域所有可能的结果个数,从而比较出了可能性的大小,是指针对准黄色区域的可能性最大,指针对准红色区域的可能性最小.
在抛掷实验中,点数小于2的面数有1个,“点数是奇数”
和“点数是偶数”
的面数各有3个,“点数大于2”的面数有4个,我们通过比较骰子面数的多少又比较出了什么呢?比较出了面朝上的点数小于2、面朝上的点数是奇数和偶数以及面朝上的点数大于2所有可能的结果个数的多少,从而比较出了可能性的大小.
综上所述,我们通过比较球的数量、扇面的数量、骰子面的数量比较出了所求事件所有可能的结果个数,实际上,我们要想比较事件发生的可能性的大小就是要比较所求事件所有可能的结果个数.
三、
拓展练习
拓展练习1:
一个转盘如图,红、黄、蓝、绿四个扇形,用力转动转盘,当转盘停止后,指针对停在某个位置,判定下列各题.
指针一定会落在绿色区域
指针落在绿色区域的可能性最大.
指针落在黄色区域的可能性小于指针落在红色区域的可能性.
分析:和前面的转盘实验相比,虽然没有全等的这些扇面了,但是我们可以对比这些度数的大小对比出可能性的大小.我们在解决问题的时候要灵活应用.
拓展练习2:
若面朝上的点数是偶数记作事件A,请你根据任意抛掷一枚骰子实验设计事件B,使事件B发生的可能性小于事件A发生的可能性.
分析:通过前面的分析我们很容易可以得到事件B可以是面朝上的点数是小于3,面朝上的点数大于4,也可以是面朝上的点数不小于5......相信同学们还会有许多不同的答案.如果老师把题目稍微变一变,不要求事件B发生的可能性小于事件A发生的可能性,而是要求事件B发生的可能性大于事件A发生的可能性呢?或者若相等呢?我们可以下课再思考思考,相信同学们可以获得许多不同的答案.
拓展练习3:
请你根据任意抛掷一枚骰子实验面朝上的点数设计两个事件,使这两个事件发生的可能性相等.
分析:要想让可能性相等,那答案可就不唯一了.答案可以是比较简单的面朝上的点数是1,面朝上的点数是2,.....,当然,也可以是面朝上的点数是3,是4,........,;还可以是面朝上的点数是1、2,面朝上的点数是3、4,...当然也可以是面朝上的点数是奇数、面朝上的点数是偶数等等.
像这样开放性的题目我们经常会遇到,同学们在得到答案后千万不要满足,而应该再试试还可以怎么想,还有哪些其他的答案,要有意识地培养自己的发散性思维能力.刚才呢我们完成了两个拓展,我们知道了事件发生的可能性是有大小的,还可能相等.我们不但会比较事件发生的可能性的大小,而且还会根据事件发生的可能性大小关系反过来设计事件.
四、
总结升华
本节课在上节课摸球实验操作及结果分析的基础上,以两个转盘实验和抛掷实验为例对随机事件发生的可能性进行研究,转盘实验,盘面上是几个全等的扇形区域,用力转,转盘停止后指针对准每个区域的机会相等,比较指针对准某种颜色区域的可能性的大小就是比较各种颜色区域的数量的多少.抛掷实验,均匀正多面体,任意掷,每个面朝上的机会相等,比较这些面出现的可能性的大小就是比较这些点数所在的面的数量的多少.
摸球实验、转盘实验、抛掷实验这三个实验都是经典的实验,通过这三个实验我们知道了事件发生的可能性是有大小的,有相等之时.比较时我们首先要确定每个结果发生的可能性是相等的,然后比较所求事件结果的个数,从而比较出可能性的大小.
其实除了这三个实验,生活中还蕴含着许多可能性的大小表述,比如说今天不大可能会下雨、小明很有可能会当选三好学生、明天我一定会准时到、他不可能再相信你.......,等等,这里我们用到不大可能,很有可能,一定,不可能,下面我们就来用这些词语填空:
用“不大可能”,“很有可能”,“一定”,“不可能”这些词语填空:
手电筒的电池没电,灯泡_________会亮.
某人是奥运会射击冠军,打把练习时_________命中10环.
天气预报说明天是晴天,因此,_________明天下雨.
如果a>b,那么a-b的值_______大于0.
在我们刚才所用的这些词语中,都是描述可能性大小的词语,都是定性的描述,那么按照可能性从小到大排列,应该是“不可能”、“不大可能”、“可能”、“很有可能”、“一定”,在生活中呢我们也要学会恰当的使用这些词语.下面我们来看一个例题.
某商场将进行一次周末有奖促销活动,共发行奖券1000张,购物满800元可抽奖券一张,其中有一等奖1名,奖笔记本一台,二等奖10名,奖自行车一辆,三等奖100名,奖乒乓球一副,幸运奖800名,奖杯子一个.
小明妈妈买了800元物品抽到一张奖券,则抽到奖的合理性描述正确的是(
)
A.不太可能抽到奖
B.很可能抽到一等奖
C.不太可能抽到一等奖
D.一定能够抽到奖
分析:我们仔细来分析一下,一等奖,二等奖三等奖和幸运奖一共是911张,奖券共1000张,也就是说在这1000张奖券中是有911张是有奖项的,说明抽到奖的可能性是非常大的,但是也有抽不到奖的可能,所以A和D这两种说法是不合理的.我们再看一等奖是1名,说明在这1000张奖券中只有一张是一等奖,那么被抽到的可能性是非常小的,所以B这个说法很明显是不合理的,而C符合常理.
以上我们说的都是常理,而实际生活中,很多事情的发生情况又是怎样的呢?我们来看几个例子
案例1.某报曾经报道过浙江省宁波和温州彩民分别中了一等奖,这两位彩民都是仅花4元钱就中了654万元的大奖.
案例2.李先生中了391万元的大奖以后,更加沉迷彩票,认为自己更多的投入一定会中更大的奖,不仅把这391万元都买了彩票反而欠下400万元外债.
这两个例子也告诉我们可能性很小的事件也可能发生,可能性很大的事件也可能不发生.在实际生活中往往就是这样,并不是所有的事情都如人愿,那我们要用平和的心态对待这些事情,要用必然和偶然的观点来看待我们的生活.
五、
课后作业
下面是代号分别为A、B、C的三个转盘,每个转盘上有四个全等的区域,颜色分布如图所示,将转盘的代号字母填在下面各题的空白处.
转动转盘______,当转盘停止后,指针对准红色区域的可能性比对准黄色区域的可能性大;
转动转盘_______,当转盘停止后,指针对准红色区域和对准黄色区域的可能性相等.
如图所示,根据题意将罐子的代号填在下面的空白:
从罐子中随意摸出一粒棋子,摸到白子的可能性大小的关系是:
从_____中摸到的可能性,大于从______中摸到的可能性,大于从_______中摸到的可能性,大于从________中摸到的可能性,大于从________中摸到的可能性.
一个均匀的正方体,6个面中有1个面是红色的、2个面是黄色的、3个面是绿色的.任意掷一次此正方体,比较下列事件发生的可能性的大小:
红色面朝上;
(2)绿色面朝上;
(3)黄色面朝上.
课题
随机事件发生的可能性(1)
教科书
书名:
数学(八年级上)
出版社:
北京出版社
出版日期:
2015
年
1
月
教学目标
教学目标:经历转盘实验和抛掷实验的分析探究的过程,在此过程中体会随机事件发生的可能性的大小的,也可能相等;会根据事件所包含的所有可能的结果的个数比较简单事件发生可能性的大小.通过实验和问题解决,感受生活中的可能性,认识到随机事件的发生与个人愿望无关,学会用必然和偶然的观点看待我们的生活.
教学重点:认识随机事件发生可能性是有大小之分、有相等之时
教学难点:比较随机事件发生的可能性大小
教学过程
时间
教学环节
主要师生活动
一、
复习回顾
同学们好,在上节课我们一起探究了一个典型实验--摸球实验,在实验过程中我们经历了动手操作、统计数据、分析结果的过程,通过对实验结果的分析我们知道球的多少与摸到的机会的大小有关系,而摸到机会的大小也即可能性的大小,随机事件发生的可能性是有大小的,是可以比较的.在比较时我们首先需要确认每个结果发生的可能性是相等的,然后可以比较所求事件包含的结果的个数,从而比较出随机事件发生的可能性的大小.
实验探究
下面我们一起来看第二个实验——抛掷实验
任意掷一个骰子,比较下列情况出现的可能性的大小.
面朝上的点数小于2;
面朝上的点数是奇数;
面朝上的点数是偶数;
面朝上的点数大于2.
相信同学们都玩过骰子,由于骰子是均匀正六面体,所以任意掷一枚骰子,每个面都有机会朝上且机会相等,6个面的点数分别是:“1点”,“2点”,“3点”,“4点”,“5点”,“6点”.因此,只需比较这些点数所在的面的数量的多少就可以比较出这些面出现的可能性的大小.
解析:因为“点数小于2”的面数只有1个,即1点.“点数是奇数”
和“点数是偶数”
的面数各有3个:1点、3点、5点和2点、4点、6点.“点数大于2”的面数有4个:3点、4点、5点、6点.所以“点数小于2”出现的可能性小于“点数是奇数”
和“点数是偶数”
出现的可能性,更小于“点数大于2”出现的可能性.其中,“点数是奇数”
和“点数是偶数”
出现的可能性相等.
下面我们来看第三个实验——转盘实验
如图是一个可以转动的转盘.盘面上有8个全等的扇形区域.其中1个是红色的,2个是白色,3个是黄色,2个是绿色.用力转动转盘,当转盘停止后:
.指针对准哪种颜色区域的可能性最小?对准哪种颜色区域的可能性最大?
.指针对准白色区域与对准绿色区域的可能性有什么关系?
分析:“全等的扇形区域”
说明指针对准每个区域的机会相等,而不是对准每种颜色的机会相等,如果区域不全等,那么指针对准每个区域的机会就不等,显然对准面积大的区域机会多,可能性大.
用力转动转盘,转盘停止后,指针对准每个区域都有相等的机会,只需比较各种颜色区域数量的多少.
.因为红色区域数量最少(1个),而黄色区域数量最多(3个),所以,指针对准红色区域的可能性最小,而对准黄色区域的可能性最大.
.由于白色区域和绿色区域的数量相等(都是2个),因此,指针对准这两种颜色区域的可能性也相等.
实验小结:
到此,我们就完成了三个典型实验,第一个实验是摸球实验,第二个实验是抛掷实验,第三个实验是转盘实验.
一般的,我们把摸出某一个球,指针对准某一个区域,骰子的某一个面朝上叫做事件发生的某一个可能的结果.而摸出每个球的可能性相等.指针对准每一个区域的可能性相等,每个面朝上的可能性均等,我们又习惯的说成每个结果发生的可能性相等.当我们确认每个结果发生的可能性相等时,我们就可以比较了.
那么在第一个实验中,我们是通过比较球的数量从而比较出了摸出白球的所有可能的结果与摸出黄球的所有可能的结果的个数,从而比较出了可能性的大小.
在第二个实验中,有红扇面1个,2个是白扇面,3个黄扇面,2个绿扇面,我们通过比较不同颜色扇面的数量又比较出了什么呢?比较出了指向黄色区域所有可能的结果个数,从而比较出了可能性的大小,是指针对准黄色区域的可能性最大,指针对准红色区域的可能性最小.
在抛掷实验中,点数小于2的面数有1个,“点数是奇数”
和“点数是偶数”
的面数各有3个,“点数大于2”的面数有4个,我们通过比较骰子面数的多少又比较出了什么呢?比较出了面朝上的点数小于2、面朝上的点数是奇数和偶数以及面朝上的点数大于2所有可能的结果个数的多少,从而比较出了可能性的大小.
综上所述,我们通过比较球的数量、扇面的数量、骰子面的数量比较出了所求事件所有可能的结果个数,实际上,我们要想比较事件发生的可能性的大小就是要比较所求事件所有可能的结果个数.
三、
拓展练习
拓展练习1:
一个转盘如图,红、黄、蓝、绿四个扇形,用力转动转盘,当转盘停止后,指针对停在某个位置,判定下列各题.
指针一定会落在绿色区域
指针落在绿色区域的可能性最大.
指针落在黄色区域的可能性小于指针落在红色区域的可能性.
分析:和前面的转盘实验相比,虽然没有全等的这些扇面了,但是我们可以对比这些度数的大小对比出可能性的大小.我们在解决问题的时候要灵活应用.
拓展练习2:
若面朝上的点数是偶数记作事件A,请你根据任意抛掷一枚骰子实验设计事件B,使事件B发生的可能性小于事件A发生的可能性.
分析:通过前面的分析我们很容易可以得到事件B可以是面朝上的点数是小于3,面朝上的点数大于4,也可以是面朝上的点数不小于5......相信同学们还会有许多不同的答案.如果老师把题目稍微变一变,不要求事件B发生的可能性小于事件A发生的可能性,而是要求事件B发生的可能性大于事件A发生的可能性呢?或者若相等呢?我们可以下课再思考思考,相信同学们可以获得许多不同的答案.
拓展练习3:
请你根据任意抛掷一枚骰子实验面朝上的点数设计两个事件,使这两个事件发生的可能性相等.
分析:要想让可能性相等,那答案可就不唯一了.答案可以是比较简单的面朝上的点数是1,面朝上的点数是2,.....,当然,也可以是面朝上的点数是3,是4,........,;还可以是面朝上的点数是1、2,面朝上的点数是3、4,...当然也可以是面朝上的点数是奇数、面朝上的点数是偶数等等.
像这样开放性的题目我们经常会遇到,同学们在得到答案后千万不要满足,而应该再试试还可以怎么想,还有哪些其他的答案,要有意识地培养自己的发散性思维能力.刚才呢我们完成了两个拓展,我们知道了事件发生的可能性是有大小的,还可能相等.我们不但会比较事件发生的可能性的大小,而且还会根据事件发生的可能性大小关系反过来设计事件.
四、
总结升华
本节课在上节课摸球实验操作及结果分析的基础上,以两个转盘实验和抛掷实验为例对随机事件发生的可能性进行研究,转盘实验,盘面上是几个全等的扇形区域,用力转,转盘停止后指针对准每个区域的机会相等,比较指针对准某种颜色区域的可能性的大小就是比较各种颜色区域的数量的多少.抛掷实验,均匀正多面体,任意掷,每个面朝上的机会相等,比较这些面出现的可能性的大小就是比较这些点数所在的面的数量的多少.
摸球实验、转盘实验、抛掷实验这三个实验都是经典的实验,通过这三个实验我们知道了事件发生的可能性是有大小的,有相等之时.比较时我们首先要确定每个结果发生的可能性是相等的,然后比较所求事件结果的个数,从而比较出可能性的大小.
其实除了这三个实验,生活中还蕴含着许多可能性的大小表述,比如说今天不大可能会下雨、小明很有可能会当选三好学生、明天我一定会准时到、他不可能再相信你.......,等等,这里我们用到不大可能,很有可能,一定,不可能,下面我们就来用这些词语填空:
用“不大可能”,“很有可能”,“一定”,“不可能”这些词语填空:
手电筒的电池没电,灯泡_________会亮.
某人是奥运会射击冠军,打把练习时_________命中10环.
天气预报说明天是晴天,因此,_________明天下雨.
如果a>b,那么a-b的值_______大于0.
在我们刚才所用的这些词语中,都是描述可能性大小的词语,都是定性的描述,那么按照可能性从小到大排列,应该是“不可能”、“不大可能”、“可能”、“很有可能”、“一定”,在生活中呢我们也要学会恰当的使用这些词语.下面我们来看一个例题.
某商场将进行一次周末有奖促销活动,共发行奖券1000张,购物满800元可抽奖券一张,其中有一等奖1名,奖笔记本一台,二等奖10名,奖自行车一辆,三等奖100名,奖乒乓球一副,幸运奖800名,奖杯子一个.
小明妈妈买了800元物品抽到一张奖券,则抽到奖的合理性描述正确的是(
)
A.不太可能抽到奖
B.很可能抽到一等奖
C.不太可能抽到一等奖
D.一定能够抽到奖
分析:我们仔细来分析一下,一等奖,二等奖三等奖和幸运奖一共是911张,奖券共1000张,也就是说在这1000张奖券中是有911张是有奖项的,说明抽到奖的可能性是非常大的,但是也有抽不到奖的可能,所以A和D这两种说法是不合理的.我们再看一等奖是1名,说明在这1000张奖券中只有一张是一等奖,那么被抽到的可能性是非常小的,所以B这个说法很明显是不合理的,而C符合常理.
以上我们说的都是常理,而实际生活中,很多事情的发生情况又是怎样的呢?我们来看几个例子
案例1.某报曾经报道过浙江省宁波和温州彩民分别中了一等奖,这两位彩民都是仅花4元钱就中了654万元的大奖.
案例2.李先生中了391万元的大奖以后,更加沉迷彩票,认为自己更多的投入一定会中更大的奖,不仅把这391万元都买了彩票反而欠下400万元外债.
这两个例子也告诉我们可能性很小的事件也可能发生,可能性很大的事件也可能不发生.在实际生活中往往就是这样,并不是所有的事情都如人愿,那我们要用平和的心态对待这些事情,要用必然和偶然的观点来看待我们的生活.
五、
课后作业
下面是代号分别为A、B、C的三个转盘,每个转盘上有四个全等的区域,颜色分布如图所示,将转盘的代号字母填在下面各题的空白处.
转动转盘______,当转盘停止后,指针对准红色区域的可能性比对准黄色区域的可能性大;
转动转盘_______,当转盘停止后,指针对准红色区域和对准黄色区域的可能性相等.
如图所示,根据题意将罐子的代号填在下面的空白:
从罐子中随意摸出一粒棋子,摸到白子的可能性大小的关系是:
从_____中摸到的可能性,大于从______中摸到的可能性,大于从_______中摸到的可能性,大于从________中摸到的可能性,大于从________中摸到的可能性.
一个均匀的正方体,6个面中有1个面是红色的、2个面是黄色的、3个面是绿色的.任意掷一次此正方体,比较下列事件发生的可能性的大小:
红色面朝上;
(2)绿色面朝上;
(3)黄色面朝上.
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
