人教版八年级上册 第十四章整式的乘法与因式分解全章复习-教学设计
文档属性
| 名称 | 人教版八年级上册 第十四章整式的乘法与因式分解全章复习-教学设计 |
|
|
| 格式 | zip | ||
| 文件大小 | 201.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-03 00:00:00 | ||
图片预览



文档简介
教学设计文本
课程基本信息
课题
整式的乘法与因式分解全章复习
教科书
书名:义务教育教科书
数学
八年级
上册
出版社:人民教育出版社
出版日期:2013年6月
教学目标
教学目标:
1.巩固整式的乘法法则,并利用整式的乘法解决有关问题;
2.通过整式的乘法运算,加深对知识的理解,建立比较清晰的知识体系.
教学重点:熟练地运用整式的乘法法则进行运算.
教学难点:灵活运用整式的乘法法则解决有关问题.
教学过程
时间
教学环节
主要师生活动
2
分钟
一、
本章知识结构
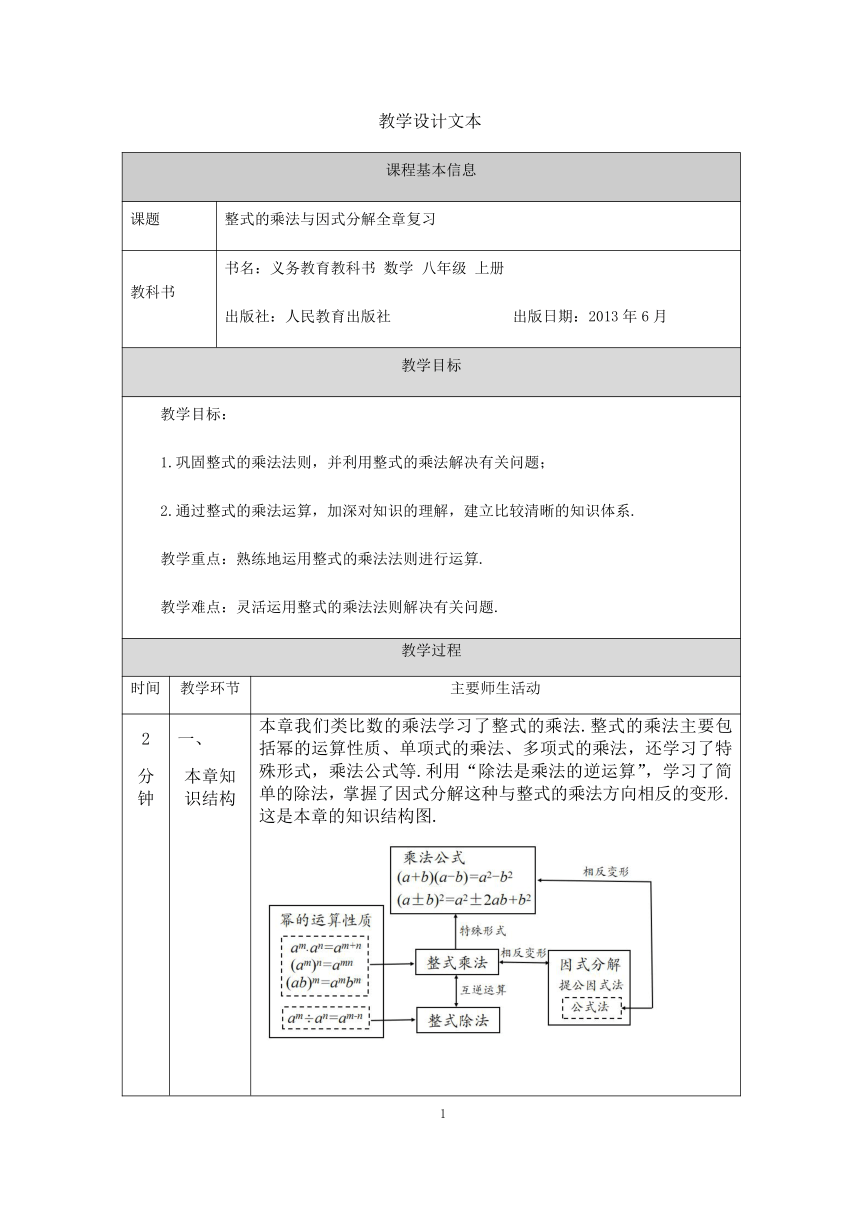
本章我们类比数的乘法学习了整式的乘法.整式的乘法主要包括幂的运算性质、单项式的乘法、多项式的乘法,还学习了特殊形式,乘法公式等.利用“除法是乘法的逆运算”,学习了简单的除法,掌握了因式分解这种与整式的乘法方向相反的变形.这是本章的知识结构图.
我们这节课主要复习整式的乘法,因式分解的具体内容下节课再复习.
22分钟
二、
典例
选讲
在整式的运算中,幂的运算是基础,有着至关重要的作用,下面我们通过具体的例题来看一下.
【例1】判断下面的计算对不对?如果不对,应该怎样改正?
(1)a2·a3=a6;
(2)(b4)3=b7;
(3)a10÷a2=a5;
(4)(-2ab2)3=-8a3b6.
【分析】
(1)明确运算法则;(2)法则具体内容.
【答案】解:(1)a2·a3=a6,×,改正:a2·a3=a5;
(2)(b4)3=b7,×,改正:(b4)3=b12;
(3)a10÷a2=a5,×,改正:a10÷a2=a8;
(4)(-2ab2)3=-8a3b6,√,(-2ab2)3=(-2)3a3(b2)3=-8a3b6.
【小结】
1.幂的运算法则:
(1)am·an=am+n(m,n都是正整数);
(2)(am)n=amn(m,n都是正整数);
(3)am÷an=am-n(a≠0,m,n都是正整数,并且m>n);
(4)(ab)n=anbn(n都是正整数).
2.使用法则时,要明确法则和具体内容.
【例2】已知10m=5,10n=3,求102m+3n的值.
【分析】
要想求102m+3n的值,可以先求m,n的值,10的多少次方等于5呢?10的多少次方等于3呢?就我们现在来说是求不出来的.观察题目中已知条件与所求值的代数式的特点,都是幂的形式,并且底数相同都是10,指数不同,用10m,10n如何表示102m+3n呢,102m+3n是指数相加的形式,我们不难想到同底数幂相乘,逆用就得到am+n=am·an,所以102m+3n=102m·103n,而102m与103n是指数相乘的形式,我们想到幂的乘方,逆用得到amn=(am)n=(an)m,102m=(10m)2,103n=(10n)3,这道题就可以解决了.
【答案】解:102m+3n=102m·103n=(10m)2·(10n)3.
将10m=5,10n=3代入,原式=52×33=675.
【巩固练习】
计算:
【分析】
运算中有乘、乘方,按照运算顺序,先算乘方,但是计算比较复杂,观察式子的特点,底数虽然不同,但是0.125与-8乘积等于-1,逆用anbn=(ab)n,但是指数需要相同,所以逆用am+n=am·an后就解决问题.
【答案】解:原式
【小结】
幂的运算算法则不仅可以正用,也可以逆用.
(1)am+n=am·an(m,n都是正整数);
(2)amn=(am)n(m,n都是正整数);
(3)am-n=am÷an(a≠0,m,n都是正整数,并且m>n);
(4)anbn=(ab)n(n都是正整数).
在复习了幂的运算的基础上,我们来看一道例题.
【例3】若定义一种新运算,a
b=2ab-b2,求x
(x+2y).
【分析】
这道题定义了一种新运算,两数
运算,它的法则是什么?=2ab-b2,也就是这两数乘积的2倍与后一个数的平方的差,转化为我们已经学过的整式的运算,关键是确定这两数.
【答案】解:(1)∵a
b=2ab-b2,
法一:
∴x
(x+2y)=2x(x+2y)-(x+2y)2
(单×多)(完全平方公式)
=2x2+4xy-(x2+4xy+4y2)
=2x2+4xy-x2-4xy-4y2
=x2-4y2;
此题是化简,结果应为一个整式,注意和因式分解结果的区别.同学们,这道题还有其他的方法化简吗?
法二:∴x
(x+2y)=2x(x+2y)-(x+2y)2
=(x+2y)[2x-(x+2y)]
=(x+2y)(2x-x-2y)
=(x+2y)(x-2y)(平方差公式)
=x2-4y2;
我们不仅可以利用整式乘法化简,也可以利用分解因式达到化简的目的.
【巩固练习】
先化简再求值:(ab+2)(ab-2)-(a2b2-4ab)÷ab,其中a=-3,b=.
分析:明确运算顺序,运算法则.按照要求对代数式先化简,运算有加、减、乘、除,按照运算顺序,先算乘除,后算加减.
解:原式=a2b2-4-(ab-4)(平方差公式)(多÷单)
=a2b2-4-ab+4
=a2b2-ab
将a=-3,b=代入,原式=(ab)2-ab=.
【小结】
1.明确运算顺序:
(1)有括号要先算括号里的;
(2)先乘方,再乘除,最后加减.
2.明确运算法则:
(1)整式的运算法则,单项式的乘除法是关键;
(2)新定义的运算法则,一般转化为学过的运算法则.
3.运算中正确使用乘法公式:
平方差公式:
(a+b)(a-b)=a2-b2;
完全平方公式:(a±b)2=a2±2ab+b2.
【例4】如图1是一个长为4b、宽为a的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成一个“回形”正方形(如图2).
(1)观察图2,请写出(a+b)2,(a-b)2,ab之间的数量关系;
(2)应用:根据(1)中的结论,若x+y=5,,求x-y的值.
【分析】
(1)结合图2,(a+b)2表示的是大正方形的面积,ab是一个小长方形的面积,而(a-b)2呢?观察图2发现,中间阴影部分的图形是正方形,边长是a-b,所以(a-b)2是中间阴影小正方形的面积.由图2发现,大正方形的面积=小正方形的面积+4个长方形的面积;
(2)由(1)得到,a+b,a-b,ab的关系,整体代入,可以解决.
【答案】解:(1)(a+b)2=(a-b)2+4ab;
(2)由(1)得:(a+b)2=(a-b)2+4ab,
∵x+y=5,,
∴52=(x-y)2+4×.
∴(x-y)2=16.
对于(a+b)2=(a-b)2+4ab这个关系,我们不仅可以通过图形之间的面积关系得到,也可以通过完全平方公式变形得到.
【小结】
完全平方公式既可以直接使用,也可以变形使用,通过这些关系式,a+b,a-b,ab,a2+b2,知二求二.
【巩固练习】
已知长方形ABCD的周长为20,面积为28,求分别以长方形的长和宽为边长的正方形面积之和是多少?
【分析】
我们一起画一下示意图,为了使条件更加直观,设长为x,宽为y,则2(x+y)=20,xy=28,要求的是x2+y2的值.直接求x,y的值,就现在的知识还不能解决,那么x2+y2,x+y,xy之间有什么关系呢?利用完全平方公式的变形,解决问题.
【答案】解:设这个长方形的长为x,宽为y,则
,
.
∴x2+y2=(x+y)2-2xy=102-2×28=44.
∴分别以长方形的长和宽为边长的
正方形面积之和是44.
1
分钟
三、
归纳
总结
这节课复习了整式的乘法,并灵活运用,相信同学们对这一章有了比较清晰的认识.
对于运算问题:明确法则,理清顺序;
使用运算法则:既可以正用,也可以逆用;既可以直接用,也可以变形用.
四、
课后
练习
1.计算:
(1)(2a)3·b4÷12a3b2;
(2)(2a+3b)(2a-b);
(3)3(y-z)2-(2y+z)(-z+2y);(4)[x(x2y2-xy)-y(x2-x3y)]÷3x2y.
2.求证:当n是整数时,两个连续奇数的平方差(2n+1)2-(2n-1)2是8的倍数.
课程基本信息
课题
整式的乘法与因式分解全章复习
教科书
书名:义务教育教科书
数学
八年级
上册
出版社:人民教育出版社
出版日期:2013年6月
教学目标
教学目标:
1.巩固整式的乘法法则,并利用整式的乘法解决有关问题;
2.通过整式的乘法运算,加深对知识的理解,建立比较清晰的知识体系.
教学重点:熟练地运用整式的乘法法则进行运算.
教学难点:灵活运用整式的乘法法则解决有关问题.
教学过程
时间
教学环节
主要师生活动
2
分钟
一、
本章知识结构
本章我们类比数的乘法学习了整式的乘法.整式的乘法主要包括幂的运算性质、单项式的乘法、多项式的乘法,还学习了特殊形式,乘法公式等.利用“除法是乘法的逆运算”,学习了简单的除法,掌握了因式分解这种与整式的乘法方向相反的变形.这是本章的知识结构图.
我们这节课主要复习整式的乘法,因式分解的具体内容下节课再复习.
22分钟
二、
典例
选讲
在整式的运算中,幂的运算是基础,有着至关重要的作用,下面我们通过具体的例题来看一下.
【例1】判断下面的计算对不对?如果不对,应该怎样改正?
(1)a2·a3=a6;
(2)(b4)3=b7;
(3)a10÷a2=a5;
(4)(-2ab2)3=-8a3b6.
【分析】
(1)明确运算法则;(2)法则具体内容.
【答案】解:(1)a2·a3=a6,×,改正:a2·a3=a5;
(2)(b4)3=b7,×,改正:(b4)3=b12;
(3)a10÷a2=a5,×,改正:a10÷a2=a8;
(4)(-2ab2)3=-8a3b6,√,(-2ab2)3=(-2)3a3(b2)3=-8a3b6.
【小结】
1.幂的运算法则:
(1)am·an=am+n(m,n都是正整数);
(2)(am)n=amn(m,n都是正整数);
(3)am÷an=am-n(a≠0,m,n都是正整数,并且m>n);
(4)(ab)n=anbn(n都是正整数).
2.使用法则时,要明确法则和具体内容.
【例2】已知10m=5,10n=3,求102m+3n的值.
【分析】
要想求102m+3n的值,可以先求m,n的值,10的多少次方等于5呢?10的多少次方等于3呢?就我们现在来说是求不出来的.观察题目中已知条件与所求值的代数式的特点,都是幂的形式,并且底数相同都是10,指数不同,用10m,10n如何表示102m+3n呢,102m+3n是指数相加的形式,我们不难想到同底数幂相乘,逆用就得到am+n=am·an,所以102m+3n=102m·103n,而102m与103n是指数相乘的形式,我们想到幂的乘方,逆用得到amn=(am)n=(an)m,102m=(10m)2,103n=(10n)3,这道题就可以解决了.
【答案】解:102m+3n=102m·103n=(10m)2·(10n)3.
将10m=5,10n=3代入,原式=52×33=675.
【巩固练习】
计算:
【分析】
运算中有乘、乘方,按照运算顺序,先算乘方,但是计算比较复杂,观察式子的特点,底数虽然不同,但是0.125与-8乘积等于-1,逆用anbn=(ab)n,但是指数需要相同,所以逆用am+n=am·an后就解决问题.
【答案】解:原式
【小结】
幂的运算算法则不仅可以正用,也可以逆用.
(1)am+n=am·an(m,n都是正整数);
(2)amn=(am)n(m,n都是正整数);
(3)am-n=am÷an(a≠0,m,n都是正整数,并且m>n);
(4)anbn=(ab)n(n都是正整数).
在复习了幂的运算的基础上,我们来看一道例题.
【例3】若定义一种新运算,a
b=2ab-b2,求x
(x+2y).
【分析】
这道题定义了一种新运算,两数
运算,它的法则是什么?=2ab-b2,也就是这两数乘积的2倍与后一个数的平方的差,转化为我们已经学过的整式的运算,关键是确定这两数.
【答案】解:(1)∵a
b=2ab-b2,
法一:
∴x
(x+2y)=2x(x+2y)-(x+2y)2
(单×多)(完全平方公式)
=2x2+4xy-(x2+4xy+4y2)
=2x2+4xy-x2-4xy-4y2
=x2-4y2;
此题是化简,结果应为一个整式,注意和因式分解结果的区别.同学们,这道题还有其他的方法化简吗?
法二:∴x
(x+2y)=2x(x+2y)-(x+2y)2
=(x+2y)[2x-(x+2y)]
=(x+2y)(2x-x-2y)
=(x+2y)(x-2y)(平方差公式)
=x2-4y2;
我们不仅可以利用整式乘法化简,也可以利用分解因式达到化简的目的.
【巩固练习】
先化简再求值:(ab+2)(ab-2)-(a2b2-4ab)÷ab,其中a=-3,b=.
分析:明确运算顺序,运算法则.按照要求对代数式先化简,运算有加、减、乘、除,按照运算顺序,先算乘除,后算加减.
解:原式=a2b2-4-(ab-4)(平方差公式)(多÷单)
=a2b2-4-ab+4
=a2b2-ab
将a=-3,b=代入,原式=(ab)2-ab=.
【小结】
1.明确运算顺序:
(1)有括号要先算括号里的;
(2)先乘方,再乘除,最后加减.
2.明确运算法则:
(1)整式的运算法则,单项式的乘除法是关键;
(2)新定义的运算法则,一般转化为学过的运算法则.
3.运算中正确使用乘法公式:
平方差公式:
(a+b)(a-b)=a2-b2;
完全平方公式:(a±b)2=a2±2ab+b2.
【例4】如图1是一个长为4b、宽为a的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成一个“回形”正方形(如图2).
(1)观察图2,请写出(a+b)2,(a-b)2,ab之间的数量关系;
(2)应用:根据(1)中的结论,若x+y=5,,求x-y的值.
【分析】
(1)结合图2,(a+b)2表示的是大正方形的面积,ab是一个小长方形的面积,而(a-b)2呢?观察图2发现,中间阴影部分的图形是正方形,边长是a-b,所以(a-b)2是中间阴影小正方形的面积.由图2发现,大正方形的面积=小正方形的面积+4个长方形的面积;
(2)由(1)得到,a+b,a-b,ab的关系,整体代入,可以解决.
【答案】解:(1)(a+b)2=(a-b)2+4ab;
(2)由(1)得:(a+b)2=(a-b)2+4ab,
∵x+y=5,,
∴52=(x-y)2+4×.
∴(x-y)2=16.
对于(a+b)2=(a-b)2+4ab这个关系,我们不仅可以通过图形之间的面积关系得到,也可以通过完全平方公式变形得到.
【小结】
完全平方公式既可以直接使用,也可以变形使用,通过这些关系式,a+b,a-b,ab,a2+b2,知二求二.
【巩固练习】
已知长方形ABCD的周长为20,面积为28,求分别以长方形的长和宽为边长的正方形面积之和是多少?
【分析】
我们一起画一下示意图,为了使条件更加直观,设长为x,宽为y,则2(x+y)=20,xy=28,要求的是x2+y2的值.直接求x,y的值,就现在的知识还不能解决,那么x2+y2,x+y,xy之间有什么关系呢?利用完全平方公式的变形,解决问题.
【答案】解:设这个长方形的长为x,宽为y,则
,
.
∴x2+y2=(x+y)2-2xy=102-2×28=44.
∴分别以长方形的长和宽为边长的
正方形面积之和是44.
1
分钟
三、
归纳
总结
这节课复习了整式的乘法,并灵活运用,相信同学们对这一章有了比较清晰的认识.
对于运算问题:明确法则,理清顺序;
使用运算法则:既可以正用,也可以逆用;既可以直接用,也可以变形用.
四、
课后
练习
1.计算:
(1)(2a)3·b4÷12a3b2;
(2)(2a+3b)(2a-b);
(3)3(y-z)2-(2y+z)(-z+2y);(4)[x(x2y2-xy)-y(x2-x3y)]÷3x2y.
2.求证:当n是整数时,两个连续奇数的平方差(2n+1)2-(2n-1)2是8的倍数.
