人教版八年级上册15.3分式方程的应用-教学设计
文档属性
| 名称 | 人教版八年级上册15.3分式方程的应用-教学设计 |
|
|
| 格式 | zip | ||
| 文件大小 | 49.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-04 15:32:06 | ||
图片预览



文档简介
课程基本信息
课题
分式方程的应用
教科书
书名:义务教育教科书
数学
八年级
上册
出版社:人民教育出版社
出版日期:
2013
年
6
月
教学目标
教学目标:使学生学会分析工程问题中的数量关系,并能通过列分式方程解应用题,掌握列分式方程解应用题的方法和步骤;培养学生分析和解决问题的能力,体会数学来源于生活,又服务于生活.
教学重点:列分式方程解决工程问题
教学难点:等量关系的提炼以及转化为方程的想法
教学过程
时间
教学环节
主要师生活动
6分
复习回顾
1.列方程解应用题的步骤
注意引导学生按照“审-设-列-解-验-答”的步骤解决问题
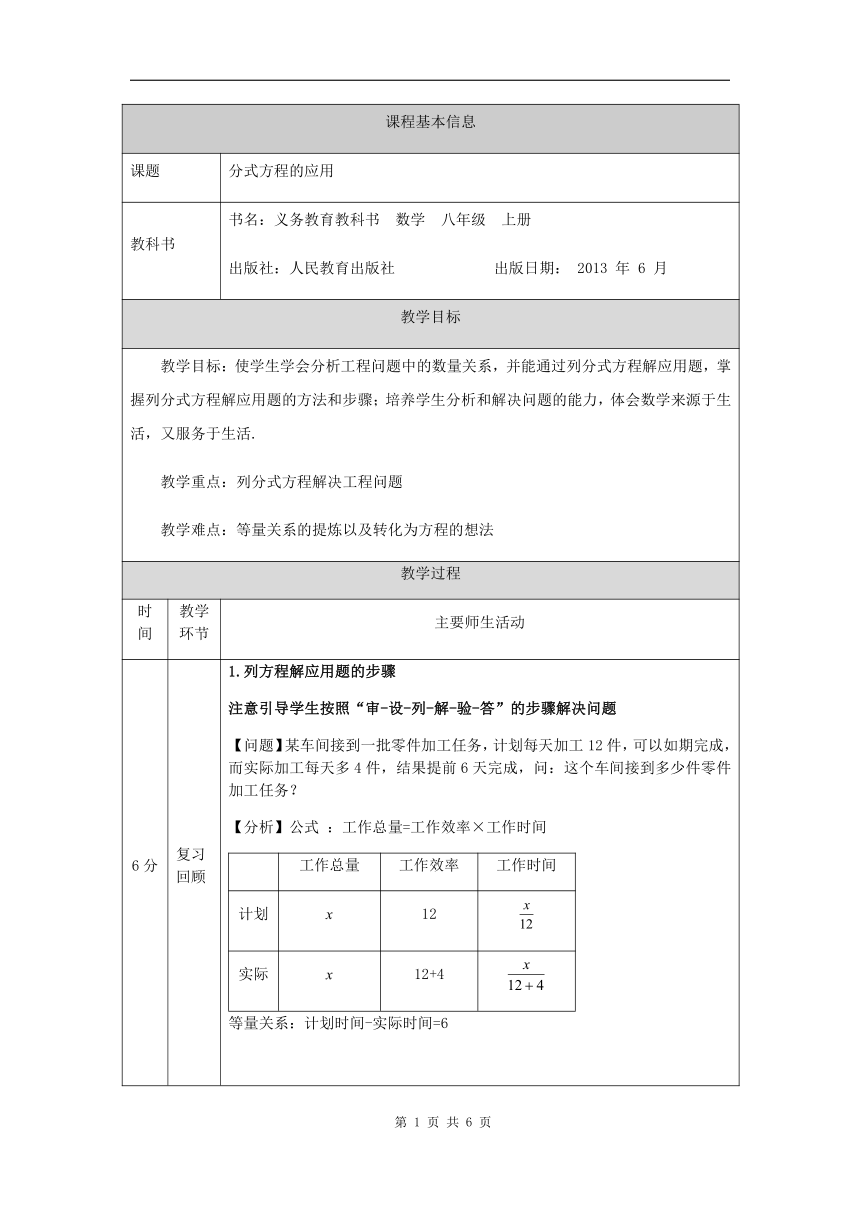
【问题】某车间接到一批零件加工任务,计划每天加工12件,可以如期完成,而实际加工每天多4件,结果提前6天完成,问:这个车间接到多少件零件加工任务?
【分析】公式
:工作总量=工作效率×工作时间
工作总量工作效率工作时间计划x12实际x12+4
等量关系:计划时间-实际时间=6
解:设这个车间接到x件零件加工任务.
解得:x=288
检验:当x=288时,左边=右边
∴x=288是方程的解,符合题意.
答:这个车间接到288件零件加工任务.
10分
探究新知
例1:两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的,这时增加了乙队,两队又共同工作了半个月,总工程全部完成.哪个队的施工速度快?
【分析】公式
:工作总量=工作效率×工作时间
工作总量工作效率工作时间甲队乙队
等量关系:甲队工作总量+乙队工作总量=1
解:设乙队的工作效率为.
两边同乘2x:x+1=2x
解得:x=1
检验:当x=1时,2x≠0
∴x=1是方程的解,符合实际.
答:乙队1个月就能完成总工程,乙队施工速度快.
引导学生按照“审-设-列-解-验-答”的步骤解决问题,强调验根的重要性.
1.审:分析题意,找出数量关系和相等关系.
2.设:选择恰当的未知数,注意单位和语言完整.
3.列:根据数量和相等关系,正确列出代数式和方程.
4.解:认真仔细.
5.验:双检验.(1)是否是所列方程的解;(2)是否符合实际意义.
6.答:注意单位和语言完整.
例2:甲乙两人做某种机械零件,已知甲每小时比乙多做6个,甲做90个的时间和乙做60个所用的时间相等,求甲、乙每小时各做零件多少个?
【分析】公式
:工作总量=工作效率×工作时间
工作总量工作效率工作时间甲90x+6乙60x
等量关系:甲做90个的时间=乙做60个的时间
解:乙每小时做x个零件.
=
两边同乘x(x+6):90x=60(x+6)
解得:x=12
检验:当x=12时,x(x+6)≠0
∴x=12是方程的解,符合实际.
答:乙每小时做12个零件,甲每小时做18个零件.
7分
巩固练习
练习:
1.张明3h清点完一批图书的一半,李强加入清点另一半图书,两人合作1.2h清点完另一半图书,如果李强单独清点这批图书需要几小时?
【分析】公式
:工作总量=工作效率×工作时间
工作总量工作效率工作时间张明0.74.2李强1.2
等量关系:张明工作总量+李强工作总量=1
解:设李强单独清点这批图书需要x小时.
两边同乘x:
解得:x=4
检验:当x=4时,x≠0
∴x=4是方程的解,符合实际.
答:李强单独清点这批图书需要4小时.
2.A、B两种机器人用来搬运化工原料,A型机器人比B型机器人每小时多搬运30kg,A型机器人搬运900kg与B型机器人搬运600kg所用时间相同,两种机器人每小时分别搬运多少kg化工原料?
【分析】公式
:工作总量=工作效率×工作时间
工作总量工作效率工作时间A900x+30B600x
等量关系:A型机器人搬运900kg时间=B型机器人搬运600kg时间
解:设B型机器人每小时搬运x
kg化工原料,A型机器人每小时搬运(x+30
)kg化工原料.
两边同乘x(x+30):900x=600(x+30)
解得:x=60
检验:当x=60时,x(x+30)≠0
∴x=60是方程的解,符合实际.
答:A型机器人每小时搬运90
kg化工原料,B型机器人每小时搬运60kg化工原料.
2分`
归纳总结
列分式方程解应用题的方法和步骤
课后作业
列方程解决实际问题:
1.某市决定修建一条从市中心到飞机场的轻轨铁路,为了使工程能提前3个月完成,需要将原定的工作效率提高12%,问原计划完成这项工程用多少月?
2.据林业专家分析,树叶在光合作用下产生的分泌物能够吸附空气中的一些悬浮颗粒物,具有滞尘净化空气的作用.已知一片银杏树叶一年的平均滞尘量比一片国槐树叶一年的平均滞尘量的2倍少4毫克,若一年滞尘1000毫克所需的银杏树叶的片数与一年滞尘550毫克所需的国槐树叶的片数相同,求一片国槐树叶一年的平均滞尘量.
课题
分式方程的应用
教科书
书名:义务教育教科书
数学
八年级
上册
出版社:人民教育出版社
出版日期:
2013
年
6
月
教学目标
教学目标:使学生学会分析工程问题中的数量关系,并能通过列分式方程解应用题,掌握列分式方程解应用题的方法和步骤;培养学生分析和解决问题的能力,体会数学来源于生活,又服务于生活.
教学重点:列分式方程解决工程问题
教学难点:等量关系的提炼以及转化为方程的想法
教学过程
时间
教学环节
主要师生活动
6分
复习回顾
1.列方程解应用题的步骤
注意引导学生按照“审-设-列-解-验-答”的步骤解决问题
【问题】某车间接到一批零件加工任务,计划每天加工12件,可以如期完成,而实际加工每天多4件,结果提前6天完成,问:这个车间接到多少件零件加工任务?
【分析】公式
:工作总量=工作效率×工作时间
工作总量工作效率工作时间计划x12实际x12+4
等量关系:计划时间-实际时间=6
解:设这个车间接到x件零件加工任务.
解得:x=288
检验:当x=288时,左边=右边
∴x=288是方程的解,符合题意.
答:这个车间接到288件零件加工任务.
10分
探究新知
例1:两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的,这时增加了乙队,两队又共同工作了半个月,总工程全部完成.哪个队的施工速度快?
【分析】公式
:工作总量=工作效率×工作时间
工作总量工作效率工作时间甲队乙队
等量关系:甲队工作总量+乙队工作总量=1
解:设乙队的工作效率为.
两边同乘2x:x+1=2x
解得:x=1
检验:当x=1时,2x≠0
∴x=1是方程的解,符合实际.
答:乙队1个月就能完成总工程,乙队施工速度快.
引导学生按照“审-设-列-解-验-答”的步骤解决问题,强调验根的重要性.
1.审:分析题意,找出数量关系和相等关系.
2.设:选择恰当的未知数,注意单位和语言完整.
3.列:根据数量和相等关系,正确列出代数式和方程.
4.解:认真仔细.
5.验:双检验.(1)是否是所列方程的解;(2)是否符合实际意义.
6.答:注意单位和语言完整.
例2:甲乙两人做某种机械零件,已知甲每小时比乙多做6个,甲做90个的时间和乙做60个所用的时间相等,求甲、乙每小时各做零件多少个?
【分析】公式
:工作总量=工作效率×工作时间
工作总量工作效率工作时间甲90x+6乙60x
等量关系:甲做90个的时间=乙做60个的时间
解:乙每小时做x个零件.
=
两边同乘x(x+6):90x=60(x+6)
解得:x=12
检验:当x=12时,x(x+6)≠0
∴x=12是方程的解,符合实际.
答:乙每小时做12个零件,甲每小时做18个零件.
7分
巩固练习
练习:
1.张明3h清点完一批图书的一半,李强加入清点另一半图书,两人合作1.2h清点完另一半图书,如果李强单独清点这批图书需要几小时?
【分析】公式
:工作总量=工作效率×工作时间
工作总量工作效率工作时间张明0.74.2李强1.2
等量关系:张明工作总量+李强工作总量=1
解:设李强单独清点这批图书需要x小时.
两边同乘x:
解得:x=4
检验:当x=4时,x≠0
∴x=4是方程的解,符合实际.
答:李强单独清点这批图书需要4小时.
2.A、B两种机器人用来搬运化工原料,A型机器人比B型机器人每小时多搬运30kg,A型机器人搬运900kg与B型机器人搬运600kg所用时间相同,两种机器人每小时分别搬运多少kg化工原料?
【分析】公式
:工作总量=工作效率×工作时间
工作总量工作效率工作时间A900x+30B600x
等量关系:A型机器人搬运900kg时间=B型机器人搬运600kg时间
解:设B型机器人每小时搬运x
kg化工原料,A型机器人每小时搬运(x+30
)kg化工原料.
两边同乘x(x+30):900x=600(x+30)
解得:x=60
检验:当x=60时,x(x+30)≠0
∴x=60是方程的解,符合实际.
答:A型机器人每小时搬运90
kg化工原料,B型机器人每小时搬运60kg化工原料.
2分`
归纳总结
列分式方程解应用题的方法和步骤
课后作业
列方程解决实际问题:
1.某市决定修建一条从市中心到飞机场的轻轨铁路,为了使工程能提前3个月完成,需要将原定的工作效率提高12%,问原计划完成这项工程用多少月?
2.据林业专家分析,树叶在光合作用下产生的分泌物能够吸附空气中的一些悬浮颗粒物,具有滞尘净化空气的作用.已知一片银杏树叶一年的平均滞尘量比一片国槐树叶一年的平均滞尘量的2倍少4毫克,若一年滞尘1000毫克所需的银杏树叶的片数与一年滞尘550毫克所需的国槐树叶的片数相同,求一片国槐树叶一年的平均滞尘量.
