人教版八年级数学上册 第十三章轴对称全章复习(第二课时) 教学设计
文档属性
| 名称 | 人教版八年级数学上册 第十三章轴对称全章复习(第二课时) 教学设计 |
|
|
| 格式 | zip | ||
| 文件大小 | 136.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-04 00:00:00 | ||
图片预览




文档简介
课程基本信息
课题
轴对称全章复习
教科书
书名:义务教育教科书
数学
八年级上册
出版社:人民教育出版社
出版日期:
2013年
6
月
教学目标
教学目标:(1)识别共顶点,等线段,等角的特殊等腰三角形的特征.
(2)经历图形演变过程,体会“从特殊到一般”,发展自己观察、比较、分析、推理的能力.
教学重点:辨别共顶点,等线段,等角的等腰三角形的特征及灵活应用.
教学难点:辨别共顶点,等线段,等角的等腰三角形的特征及灵活应用.
教学过程
时间
教学环节
主要师生活动
8分钟
6分钟
6分钟
3分钟
1分钟
1分钟
环节一
环节二
环节三
环节四
环节五
环节六
各位同学,等腰三角形都有哪些性质?
追问:等边三角形都有哪些性质呢?
通过之前的学习,我们发现两个共顶点的等边三角形会产生一对全等三角形,接下来我们来看下面一道例题:
类型一
共顶点的等边三角形
1、如图,△和△均为等边三角形,并且点、、在一条直线上,连接、交于点,
求证:①
;
②
与之间的夹角为.
【分析】①两线段相等,可以联想到的证明方法一般有:一是同一三角形中可以通过两角相等证得两线段相等;二是通过两个三角形全等证得两线段相等;三是通过中间量的代换证得两线段相等。
通过对题干的分析发现,线段AE和DB分属不同的三角形,可以从全等的角度寻求解决问题的途径。有了此思路,可以找三角形全等的条件,通过分析可以证得△≌△(SAS),所以.
②充分根据①的全等,找到角等,然后根据8字倒角得到∠AOB=∠ACB.
【解答】
证:①
△≌△(SAS),所以;
②△≌△(SAS)
∠EAC=∠DBC
∠AFO=∠BFC
∠AOB=∠ACB=;
【变式】
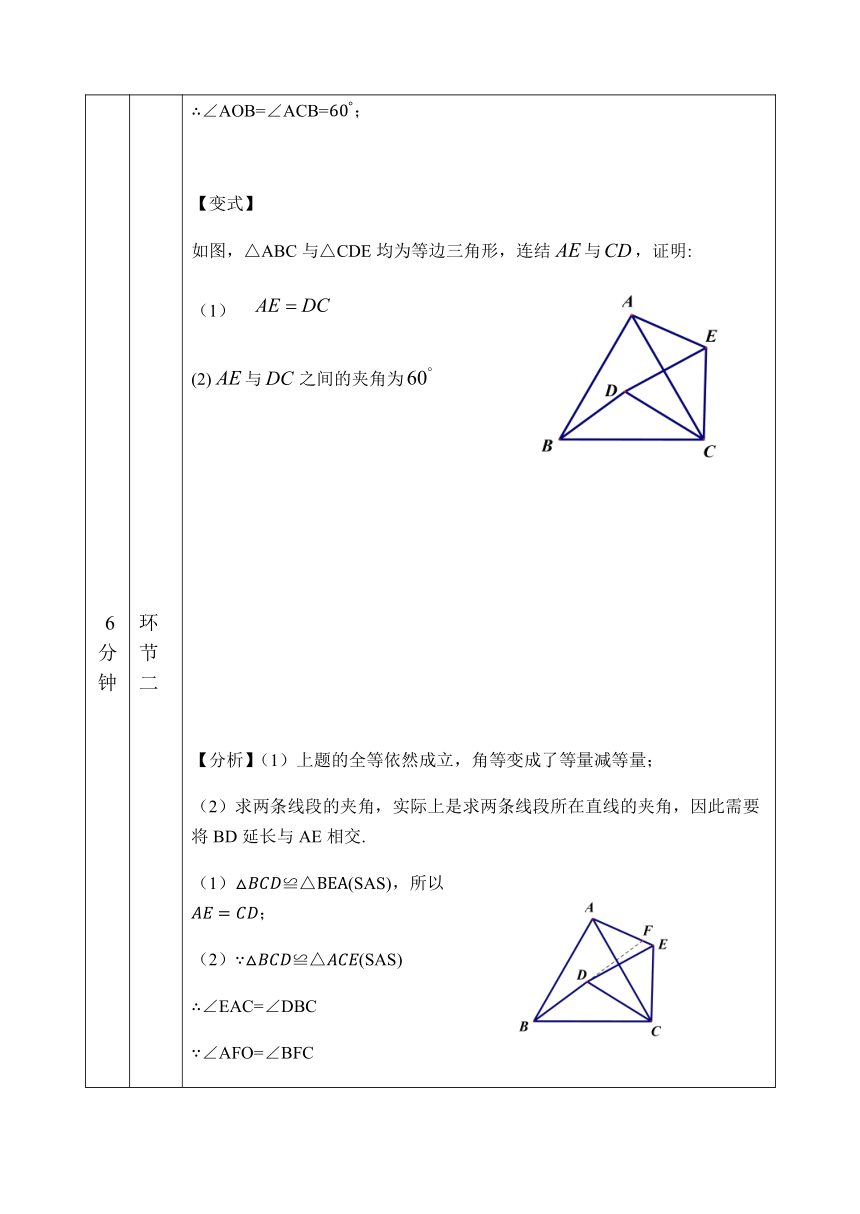
如图,△ABC与△CDE均为等边三角形,连结与,证明:
(2)与之间的夹角为
【分析】(1)上题的全等依然成立,角等变成了等量减等量;
(2)求两条线段的夹角,实际上是求两条线段所在直线的夹角,因此需要将BD延长与AE相交.
(1)△≌△(SAS),所以;
(2)△≌△(SAS)
∠EAC=∠DBC
∠AFO=∠BFC
∠AOB=∠ACB=;
图形特征总结:这个图形是由两个共顶点的等边三角形构成,在相对位置变化的同时,始终存在一对全等三角形.
请问,等腰直角三角形都有什么性质呢?
答:①两直角边相等;
②顶角等于90°,底角等于45°;
③“三线合一”.
我们进一步思考,除了等边三角形,等腰直角三角形是否也有上述类似的结论呢?
类型二
共顶点的等腰直角三角形
【例题】如图,△ADC与△EDG都为等腰直角三角形,连接AG、CE,相交于点H,问:
(1)AG与CE是否相等?
(2)AG与CE之间的夹角为多少度?
解答:
(1)AG=CE.理由如下:
∵∠ADG=∠ADC+∠CDG,∠CDE=∠GDE+∠CDG,
∠ADC=∠EDG=90°,
∴∠ADG=∠CDE.
在△ADG和△CDE中,
∴△ADE≌△CDE.
∴AG=CE.
(2)∵△ADG≌△CDE,
∴∠DAG=∠DCE.
∵∠COH=∠AOD,
∴∠CHA=∠ADC=90°.
∴AG与CE之间的夹角是90°.
总结:解题经验:共直角顶点的等腰直角和共顶点的等边三角形,往往利用相等边长和等角构造全等三角形.
归纳的典型特征:共顶点,等线段,顶角度数相等.体会图形变化中的不变量.
思考:通过今天的学习,你可以把这些基本结论再拓展到更一般的等腰三角形的范围吗?你还能发现什么样的结论?
如果时间来得及就分析一下第1个,如果时间来不及,就把它作为学生课下的思考题.
模型分析:
如图①,
∠BAD=∠BAC-∠DAC,∠CAE=∠DAE-∠DAC.
∵∠BAC=∠DAE=,
∴∠BAD=∠CAE.
在△BAD和△CAE中,
∴△BAD≌△CAE.
方法总结:共顶点,等线段,顶角度数相等的
两个等腰三角形,在相对位置变化的同时,始终存在一对
全等三角形.
小结:
从特殊到一般.
作业:
1、如图两个等边三角形与,连结与,
证明:(1)AE=CD;
(2)AE与DC之间的夹角为.
2、如图,在△ABC中,AB=CB,∠BAC=∠BCA,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.
(1)求证:Rt△ABE≌Rt△CBF;
(2)求证:AE⊥CF;
(3)若∠CAE=30°,求∠ACF度数.
【点睛】(1)由“HL”可证Rt△ABE≌Rt△CBF;
(2)根据Rt△ABE≌Rt△CBF,可以得到∠BCF=∠BAE,由直角三角形的性质可得结论;
(3)由三角形内角和定理可以得到∠ACF的度数.
【解析】证明:(1)∵∠ABC=90°,
∴∠ABE=∠CBF=90°,
在Rt△ABE和Rt△CBF中,
,
∴Rt△ABE≌Rt△CBF(HL);
(2)如图,
∵Rt△ABE≌Rt△CBF,
∴∠BCF=∠BAE,
∵∠BCF+∠F=90°,
∴∠BAE+∠F=90°,
∴∠AHF=90°,
∴AF⊥CF;
(3)∵∠AHF=90°,∠EAC=30°,
∴∠ACF=60°.
课题
轴对称全章复习
教科书
书名:义务教育教科书
数学
八年级上册
出版社:人民教育出版社
出版日期:
2013年
6
月
教学目标
教学目标:(1)识别共顶点,等线段,等角的特殊等腰三角形的特征.
(2)经历图形演变过程,体会“从特殊到一般”,发展自己观察、比较、分析、推理的能力.
教学重点:辨别共顶点,等线段,等角的等腰三角形的特征及灵活应用.
教学难点:辨别共顶点,等线段,等角的等腰三角形的特征及灵活应用.
教学过程
时间
教学环节
主要师生活动
8分钟
6分钟
6分钟
3分钟
1分钟
1分钟
环节一
环节二
环节三
环节四
环节五
环节六
各位同学,等腰三角形都有哪些性质?
追问:等边三角形都有哪些性质呢?
通过之前的学习,我们发现两个共顶点的等边三角形会产生一对全等三角形,接下来我们来看下面一道例题:
类型一
共顶点的等边三角形
1、如图,△和△均为等边三角形,并且点、、在一条直线上,连接、交于点,
求证:①
;
②
与之间的夹角为.
【分析】①两线段相等,可以联想到的证明方法一般有:一是同一三角形中可以通过两角相等证得两线段相等;二是通过两个三角形全等证得两线段相等;三是通过中间量的代换证得两线段相等。
通过对题干的分析发现,线段AE和DB分属不同的三角形,可以从全等的角度寻求解决问题的途径。有了此思路,可以找三角形全等的条件,通过分析可以证得△≌△(SAS),所以.
②充分根据①的全等,找到角等,然后根据8字倒角得到∠AOB=∠ACB.
【解答】
证:①
△≌△(SAS),所以;
②△≌△(SAS)
∠EAC=∠DBC
∠AFO=∠BFC
∠AOB=∠ACB=;
【变式】
如图,△ABC与△CDE均为等边三角形,连结与,证明:
(2)与之间的夹角为
【分析】(1)上题的全等依然成立,角等变成了等量减等量;
(2)求两条线段的夹角,实际上是求两条线段所在直线的夹角,因此需要将BD延长与AE相交.
(1)△≌△(SAS),所以;
(2)△≌△(SAS)
∠EAC=∠DBC
∠AFO=∠BFC
∠AOB=∠ACB=;
图形特征总结:这个图形是由两个共顶点的等边三角形构成,在相对位置变化的同时,始终存在一对全等三角形.
请问,等腰直角三角形都有什么性质呢?
答:①两直角边相等;
②顶角等于90°,底角等于45°;
③“三线合一”.
我们进一步思考,除了等边三角形,等腰直角三角形是否也有上述类似的结论呢?
类型二
共顶点的等腰直角三角形
【例题】如图,△ADC与△EDG都为等腰直角三角形,连接AG、CE,相交于点H,问:
(1)AG与CE是否相等?
(2)AG与CE之间的夹角为多少度?
解答:
(1)AG=CE.理由如下:
∵∠ADG=∠ADC+∠CDG,∠CDE=∠GDE+∠CDG,
∠ADC=∠EDG=90°,
∴∠ADG=∠CDE.
在△ADG和△CDE中,
∴△ADE≌△CDE.
∴AG=CE.
(2)∵△ADG≌△CDE,
∴∠DAG=∠DCE.
∵∠COH=∠AOD,
∴∠CHA=∠ADC=90°.
∴AG与CE之间的夹角是90°.
总结:解题经验:共直角顶点的等腰直角和共顶点的等边三角形,往往利用相等边长和等角构造全等三角形.
归纳的典型特征:共顶点,等线段,顶角度数相等.体会图形变化中的不变量.
思考:通过今天的学习,你可以把这些基本结论再拓展到更一般的等腰三角形的范围吗?你还能发现什么样的结论?
如果时间来得及就分析一下第1个,如果时间来不及,就把它作为学生课下的思考题.
模型分析:
如图①,
∠BAD=∠BAC-∠DAC,∠CAE=∠DAE-∠DAC.
∵∠BAC=∠DAE=,
∴∠BAD=∠CAE.
在△BAD和△CAE中,
∴△BAD≌△CAE.
方法总结:共顶点,等线段,顶角度数相等的
两个等腰三角形,在相对位置变化的同时,始终存在一对
全等三角形.
小结:
从特殊到一般.
作业:
1、如图两个等边三角形与,连结与,
证明:(1)AE=CD;
(2)AE与DC之间的夹角为.
2、如图,在△ABC中,AB=CB,∠BAC=∠BCA,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.
(1)求证:Rt△ABE≌Rt△CBF;
(2)求证:AE⊥CF;
(3)若∠CAE=30°,求∠ACF度数.
【点睛】(1)由“HL”可证Rt△ABE≌Rt△CBF;
(2)根据Rt△ABE≌Rt△CBF,可以得到∠BCF=∠BAE,由直角三角形的性质可得结论;
(3)由三角形内角和定理可以得到∠ACF的度数.
【解析】证明:(1)∵∠ABC=90°,
∴∠ABE=∠CBF=90°,
在Rt△ABE和Rt△CBF中,
,
∴Rt△ABE≌Rt△CBF(HL);
(2)如图,
∵Rt△ABE≌Rt△CBF,
∴∠BCF=∠BAE,
∵∠BCF+∠F=90°,
∴∠BAE+∠F=90°,
∴∠AHF=90°,
∴AF⊥CF;
(3)∵∠AHF=90°,∠EAC=30°,
∴∠ACF=60°.
