人教版九年级数学下册 第28章28.1--28.2 基础达标检测题(word版,含答案)
文档属性
| 名称 | 人教版九年级数学下册 第28章28.1--28.2 基础达标检测题(word版,含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 251.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-04 00:00:00 | ||
图片预览




文档简介
人教版九年级数学下册
28.1
一.选择题(本大题共10小题,每小题3分,共30分)
1.如图,在Rt△ABC中,∠C=90°,若AB=10,AC=8,则sinA等于(
)
A. B. C. D.
2.在直角三角形ABC中,若各边的长都扩大到原来的5倍,则∠A的正弦值(
)
A.扩大到原来的5倍
B.缩小到原来的
C.不变
D.不能确定
3.在Rt△ABC中,∠C=90°,AB=BC,则sinB的值为(
)
A.
B.
C.
D.1
4.
如图,在Rt△ABC中,∠C=90°,AB=13,BC=12,则下列表示正确的是(
)
A.sin
A=
B.cos
A=
C.tan
A=
D.tan
B=
5.在正方形网格中,△ABC的位置如图,则sin
B的值为(
)
A.
B.
C.
D.
6.如图,CD是Rt△ABC的高,∠ACB=90°,下列用线段比表示sin
α的值,错误的是(
)
A.
B.
C.
D.
7.在Rt△ABC中,∠C=90°,sinA=,BC=6,则AB=(
)
A.4
B.6
C.8
D.10
8.在Rt△ABC中,∠C=90°,若AB=4,sinA=,则斜边上的高等于(
)
A.
B.
C.
D.
9.
如图,在5×4的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在这些小正方形的顶点上,则sin∠BAC的值为(
)
A.
B.
C.
D.
10.
如图,点D(0,3),O(0,0),C(4,0)在⊙A上,BD是⊙A的一条弦,则sin∠OBD=(
)
A.
B.
C.
D.
二.填空题(共8小题,3
8=24)
11.
如图,若点A的坐标为(1,),则sin∠α=_____.
12.在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,CD=4,AC=6,则sinB的值是_______.
13.如图,菱形ABCD的边长为15,sin∠BAC=,则对角线AC的长为_____.
14.如图,在⊙O中,过直径AB延长线上的点C作⊙O的一条切线,切点为D,若AC=7,AB=4,则sinC的值为______.
15.如图,已知直线l1∥l2∥l3∥l4,相邻两条平行直线间的距离都是1,如果正方形ABCD的四个顶点分别在四条直线上,那么sinα=_____.
16.
如图,△ABC的顶点都在正方形网格的格点上,则cos
C=
.
17.
如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,则sin
A=_______,sin
B=_________.
18.
如图,则图中∠A的正弦值分别是___________、__________.
三.解答题(共7小题,46分)
19.(6分)
如图,⊙O的半径为3,弦AB的长为4.求sinA的值.
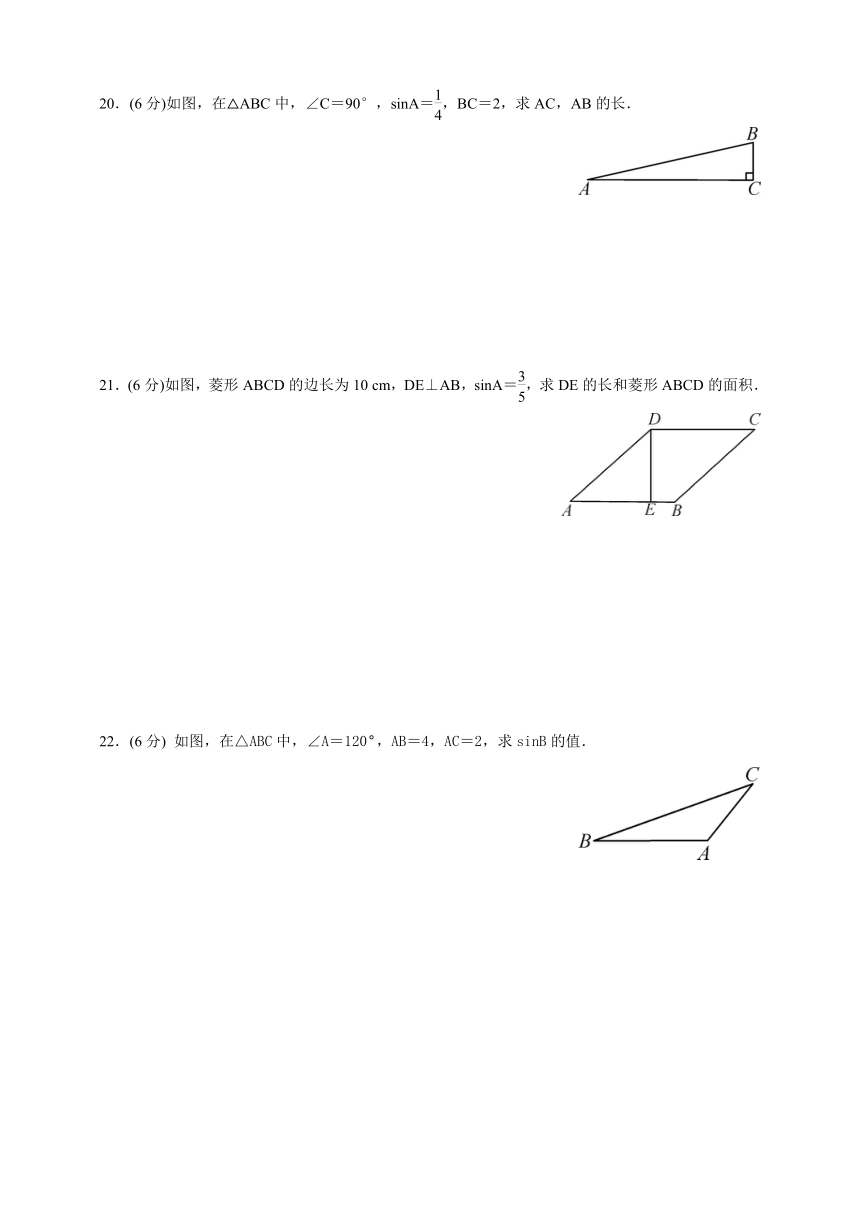
20.(6分)如图,在△ABC中,∠C=90°,sinA=,BC=2,求AC,AB的长.
21.(6分)如图,菱形ABCD的边长为10
cm,DE⊥AB,sinA=,求DE的长和菱形ABCD的面积.
22.(6分)
如图,在△ABC中,∠A=120°,AB=4,AC=2,求sinB的值.
23.(6分)
如图,网格中的每个小正方形的边长都是1,△ABC每个顶点都在网格的交点处,求sinA的值.
24.(8分)
如图,AB是半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于D,连接BE.设∠BEC=α,求sinα的值.
25.(8分)
如图,CD是Rt△ABC的高,∠ACB=90°,BC=10,sin∠DCA=,求CD的长.
参考答案:
1-5ACBAB
6-10DDBDD
11.
12.
13.
24
14.
15.
16.
17.
,
18.
,
19.
解:过点O作OC⊥AB于点C,则有AC=BC,
∵AB=4,∴AC=2,
在Rt△AOC中,OC===,
∴sinA==
20.
解:∵sinA=,∴=,
∴AB=4BC=4×2=8,
∴AC===2
21.
解:∵DE⊥AB,∴∠AED=90°,
在Rt△AED中,sinA=,
即=,解得DE=6
cm,
∴菱形ABCD的面积为10×6=60(cm2)
22.
解:作CD⊥AB于点D,∴∠ADC=90°,
∵∠BAC=120°,∴∠DAC=180°-∠BAC=60°,
在Rt△ADC中,AC=2,∴AD=1,CD=,∴BD=5,
在Rt△BCD中,BC==2,
∴sinB===
23.
解:作AD⊥BC于点D,CE⊥AB于点E,
由勾股定理得AB=AC=2,BC=2,AD=3,
由BC·AD=AB·CE,得CE==,
∴sinA===
24.
解:连接BC,∵AB是半圆的直径,∴∠ACB=90°,
在Rt△ABC中,AC=8,AB=10,
∴BC==6,∵OD⊥AC,
∴AE=CE=AC=4,
在Rt△BCE中,BE==2,
∴sinα===
25.
解:∵CD是Rt△ABC的高,∠ACB=90°,
∴∠DCA+∠A=90°,
∠A+∠B=90°,
∴∠B=∠DCA.
∵sin∠DCA=,∴sin
B=,
∴=.
∵BC=10,∴CD=4.
28.2.1解直角三角形
一、基础训练
1.在Rt△ABC中,∠C=900,∠A、∠B、∠C的对边分别为a、b、c,那么
(1)三边之间的关系为
;(2)锐角之间的关系为
;
(3)边角之间的关系为
.
2.填空:在Rt△ABC中,∠C=90°,(1)已知a=4,b=8,则c=
,
(2)已知b=10,∠B=60°,则a=
,c=
.
(3)已知c=20,∠A=60°,则a=
,b=
.
3.已知等腰△ABC中,AB=AC=13,BC=10,则sinB=
,cosB=
,tanC=
.
4.在△ABC中,∠C=90°,a=3,b=3,则∠A=
°,边c=
.
二、典型例题
例1.由下列条件解直角三角形:在Rt△ABC中,∠C=90°:
(1)
已知c=20,∠A=45°;
(2)
已知a+c=12,∠B=60°
分析
利用三角函数进行计算.
例2.如图所示,平地上一棵树高为5米,两次观察地面上的影子,第一次是当阳光与地面成45°时,第二次是阳光与地面成30°时,第二次观察点与第一次观察点的距离是多少米?
分析
利用30°、45°的正切进行计算,再相减即可.
三、拓展提升
某省计划将地处A、B两地的两所大学合并成一所综合性大学,为了方便两地师生交往,学校准备在相距2km的A、B两地之间修一条笔直的公路,经测量在A地北偏东600方向,B地北偏西450方向的C处有一个半径为0.7km的公园,问计划修筑的这条公路会不会穿过公园?为什么?
分析
过C作AB的垂线,垂足为D,计算出CD的长,如果
CD>0.7km,则不会穿过公园,如果CD<0.7km,则穿过公园.
四、课后作业
1.在Rt△ABC中,∠C=90°,当已知∠A和a时,求c,则∠A、a、c关系式是c=
.
2.在Rt△ABC中,∠C=900,∠A=300,b=,则a=
,c=
.
3.已知在直角梯形ABCD中,上底CD=4,下底AB=10,非直角腰BC=,则底角∠B=
.
4.若∠A是锐角,且cosA=,则cos(900—A)=
.
5.在△ABC中,∠C=90°,
(1)已知∠A=30°,BC=8cm,求AB与AC的长;
(2)已知∠A=60°,AC=cm,求AB与BC的长.
6.设直线y=x3与x轴所成的锐角为α,试求锐角α.
7.Rt△ABC中,∠C=90°,∠B=60°,两直角边的和为14,求这个直角三角形的面积.
8.如图,在△ABC中,∠C=90,∠BAC=30,延长CA至D,使AD=AB,试由图求tan15的值.
答案
一、基础训练
1.
(1)a2
+
b2
=c2
(2)∠A
+
∠B=90°(3)
sinA=cosB=
cosA=sinB=
tanA=
tanB=
2.(1)
4(2)
(3)
10
10
3.
sinB=
cosB=
tanC=
4.
30°6
二、典型例题
例1
(1)∠B=45°
a=b=10
(2)
∠C=30°a=4
b=4
c=8
例2
5-
5
三、拓展提升
点C到AB的距离约为0.8082km>0.7km,所以不会穿过公园.
四、课后作业
1.
2.
a=10
c=20
3.30°
4.
5.
(1)AB=8
AC=16
(2)
AB=2
AC=3
6.
60°
7.面积为98-147
8.
2
-
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
28.1
一.选择题(本大题共10小题,每小题3分,共30分)
1.如图,在Rt△ABC中,∠C=90°,若AB=10,AC=8,则sinA等于(
)
A. B. C. D.
2.在直角三角形ABC中,若各边的长都扩大到原来的5倍,则∠A的正弦值(
)
A.扩大到原来的5倍
B.缩小到原来的
C.不变
D.不能确定
3.在Rt△ABC中,∠C=90°,AB=BC,则sinB的值为(
)
A.
B.
C.
D.1
4.
如图,在Rt△ABC中,∠C=90°,AB=13,BC=12,则下列表示正确的是(
)
A.sin
A=
B.cos
A=
C.tan
A=
D.tan
B=
5.在正方形网格中,△ABC的位置如图,则sin
B的值为(
)
A.
B.
C.
D.
6.如图,CD是Rt△ABC的高,∠ACB=90°,下列用线段比表示sin
α的值,错误的是(
)
A.
B.
C.
D.
7.在Rt△ABC中,∠C=90°,sinA=,BC=6,则AB=(
)
A.4
B.6
C.8
D.10
8.在Rt△ABC中,∠C=90°,若AB=4,sinA=,则斜边上的高等于(
)
A.
B.
C.
D.
9.
如图,在5×4的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在这些小正方形的顶点上,则sin∠BAC的值为(
)
A.
B.
C.
D.
10.
如图,点D(0,3),O(0,0),C(4,0)在⊙A上,BD是⊙A的一条弦,则sin∠OBD=(
)
A.
B.
C.
D.
二.填空题(共8小题,3
8=24)
11.
如图,若点A的坐标为(1,),则sin∠α=_____.
12.在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,CD=4,AC=6,则sinB的值是_______.
13.如图,菱形ABCD的边长为15,sin∠BAC=,则对角线AC的长为_____.
14.如图,在⊙O中,过直径AB延长线上的点C作⊙O的一条切线,切点为D,若AC=7,AB=4,则sinC的值为______.
15.如图,已知直线l1∥l2∥l3∥l4,相邻两条平行直线间的距离都是1,如果正方形ABCD的四个顶点分别在四条直线上,那么sinα=_____.
16.
如图,△ABC的顶点都在正方形网格的格点上,则cos
C=
.
17.
如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,则sin
A=_______,sin
B=_________.
18.
如图,则图中∠A的正弦值分别是___________、__________.
三.解答题(共7小题,46分)
19.(6分)
如图,⊙O的半径为3,弦AB的长为4.求sinA的值.
20.(6分)如图,在△ABC中,∠C=90°,sinA=,BC=2,求AC,AB的长.
21.(6分)如图,菱形ABCD的边长为10
cm,DE⊥AB,sinA=,求DE的长和菱形ABCD的面积.
22.(6分)
如图,在△ABC中,∠A=120°,AB=4,AC=2,求sinB的值.
23.(6分)
如图,网格中的每个小正方形的边长都是1,△ABC每个顶点都在网格的交点处,求sinA的值.
24.(8分)
如图,AB是半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于D,连接BE.设∠BEC=α,求sinα的值.
25.(8分)
如图,CD是Rt△ABC的高,∠ACB=90°,BC=10,sin∠DCA=,求CD的长.
参考答案:
1-5ACBAB
6-10DDBDD
11.
12.
13.
24
14.
15.
16.
17.
,
18.
,
19.
解:过点O作OC⊥AB于点C,则有AC=BC,
∵AB=4,∴AC=2,
在Rt△AOC中,OC===,
∴sinA==
20.
解:∵sinA=,∴=,
∴AB=4BC=4×2=8,
∴AC===2
21.
解:∵DE⊥AB,∴∠AED=90°,
在Rt△AED中,sinA=,
即=,解得DE=6
cm,
∴菱形ABCD的面积为10×6=60(cm2)
22.
解:作CD⊥AB于点D,∴∠ADC=90°,
∵∠BAC=120°,∴∠DAC=180°-∠BAC=60°,
在Rt△ADC中,AC=2,∴AD=1,CD=,∴BD=5,
在Rt△BCD中,BC==2,
∴sinB===
23.
解:作AD⊥BC于点D,CE⊥AB于点E,
由勾股定理得AB=AC=2,BC=2,AD=3,
由BC·AD=AB·CE,得CE==,
∴sinA===
24.
解:连接BC,∵AB是半圆的直径,∴∠ACB=90°,
在Rt△ABC中,AC=8,AB=10,
∴BC==6,∵OD⊥AC,
∴AE=CE=AC=4,
在Rt△BCE中,BE==2,
∴sinα===
25.
解:∵CD是Rt△ABC的高,∠ACB=90°,
∴∠DCA+∠A=90°,
∠A+∠B=90°,
∴∠B=∠DCA.
∵sin∠DCA=,∴sin
B=,
∴=.
∵BC=10,∴CD=4.
28.2.1解直角三角形
一、基础训练
1.在Rt△ABC中,∠C=900,∠A、∠B、∠C的对边分别为a、b、c,那么
(1)三边之间的关系为
;(2)锐角之间的关系为
;
(3)边角之间的关系为
.
2.填空:在Rt△ABC中,∠C=90°,(1)已知a=4,b=8,则c=
,
(2)已知b=10,∠B=60°,则a=
,c=
.
(3)已知c=20,∠A=60°,则a=
,b=
.
3.已知等腰△ABC中,AB=AC=13,BC=10,则sinB=
,cosB=
,tanC=
.
4.在△ABC中,∠C=90°,a=3,b=3,则∠A=
°,边c=
.
二、典型例题
例1.由下列条件解直角三角形:在Rt△ABC中,∠C=90°:
(1)
已知c=20,∠A=45°;
(2)
已知a+c=12,∠B=60°
分析
利用三角函数进行计算.
例2.如图所示,平地上一棵树高为5米,两次观察地面上的影子,第一次是当阳光与地面成45°时,第二次是阳光与地面成30°时,第二次观察点与第一次观察点的距离是多少米?
分析
利用30°、45°的正切进行计算,再相减即可.
三、拓展提升
某省计划将地处A、B两地的两所大学合并成一所综合性大学,为了方便两地师生交往,学校准备在相距2km的A、B两地之间修一条笔直的公路,经测量在A地北偏东600方向,B地北偏西450方向的C处有一个半径为0.7km的公园,问计划修筑的这条公路会不会穿过公园?为什么?
分析
过C作AB的垂线,垂足为D,计算出CD的长,如果
CD>0.7km,则不会穿过公园,如果CD<0.7km,则穿过公园.
四、课后作业
1.在Rt△ABC中,∠C=90°,当已知∠A和a时,求c,则∠A、a、c关系式是c=
.
2.在Rt△ABC中,∠C=900,∠A=300,b=,则a=
,c=
.
3.已知在直角梯形ABCD中,上底CD=4,下底AB=10,非直角腰BC=,则底角∠B=
.
4.若∠A是锐角,且cosA=,则cos(900—A)=
.
5.在△ABC中,∠C=90°,
(1)已知∠A=30°,BC=8cm,求AB与AC的长;
(2)已知∠A=60°,AC=cm,求AB与BC的长.
6.设直线y=x3与x轴所成的锐角为α,试求锐角α.
7.Rt△ABC中,∠C=90°,∠B=60°,两直角边的和为14,求这个直角三角形的面积.
8.如图,在△ABC中,∠C=90,∠BAC=30,延长CA至D,使AD=AB,试由图求tan15的值.
答案
一、基础训练
1.
(1)a2
+
b2
=c2
(2)∠A
+
∠B=90°(3)
sinA=cosB=
cosA=sinB=
tanA=
tanB=
2.(1)
4(2)
(3)
10
10
3.
sinB=
cosB=
tanC=
4.
30°6
二、典型例题
例1
(1)∠B=45°
a=b=10
(2)
∠C=30°a=4
b=4
c=8
例2
5-
5
三、拓展提升
点C到AB的距离约为0.8082km>0.7km,所以不会穿过公园.
四、课后作业
1.
2.
a=10
c=20
3.30°
4.
5.
(1)AB=8
AC=16
(2)
AB=2
AC=3
6.
60°
7.面积为98-147
8.
2
-
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
