25.6相似三角形的应用(1)-冀教版九年级数学上册导学案(含答案)
文档属性
| 名称 | 25.6相似三角形的应用(1)-冀教版九年级数学上册导学案(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-04 00:00:00 | ||
图片预览

文档简介
九年级数学教案(编号20)
课题: 25.6相似三角形的应用 备课人: 编制日期:
使用日期: 学科组长签字: 分管领导签字:
学习目标:1.经历对实际问题的探索,会利用相似三角形的性质测量物体的高度或距离.
2.在具体情境中建立数学模型,并综合运用数学知识解决简单实际问题.
一、知识链接:【师生活动】 学生独立思考回答,教师规范书写.
1.要测量不可直接到达的A、B两点距离,在O点设柱,取OA中点C,取OB中点D,测得CD=25m,则AB= 。
2.铁道栏杆短臂长1米,长臂长16米,当短臂端点下降0.5米,长臂升高 米。
3、在比例尺为1:3000的地图上,一个三角形的周长是4cm,面积为1cm2,则它的实际面积为 m2, 它的实际周长为 m。
4、如图,在直角梯形ABCD中,DC∥AB,∠DAB=90°,AC⊥BC,AC=BC,∠ABC的平分线分别交AD、AC于点E,F,则的值是( )
A.
1134110263525C
D
A
B
C
D
A
B
-1270309880D
C
O
A
B
D
C
O
A
B
B.
C.
67945326390
D.
二、新知探究:【师生活动】学生自主学习、独立思考后,小组合作交流,学生展示后教师点评归纳,.
42710103778251、如图,九年级(1)班课外活动小组利用标杆测量学校旗杆的高度,已知标杆高度CD=3m,标杆与旗杆的水平距离BD=15m,人的眼睛与地面的高度EF=1.6m,人与标杆CD的水平距离DF=2m,求旗杆AB的高度.
三、典例分析:【师生活动】 学生独立思考后,小组合作交流,教师对有困难的学生进行指导,小组代表展示,教师点评过程中强调易错点.
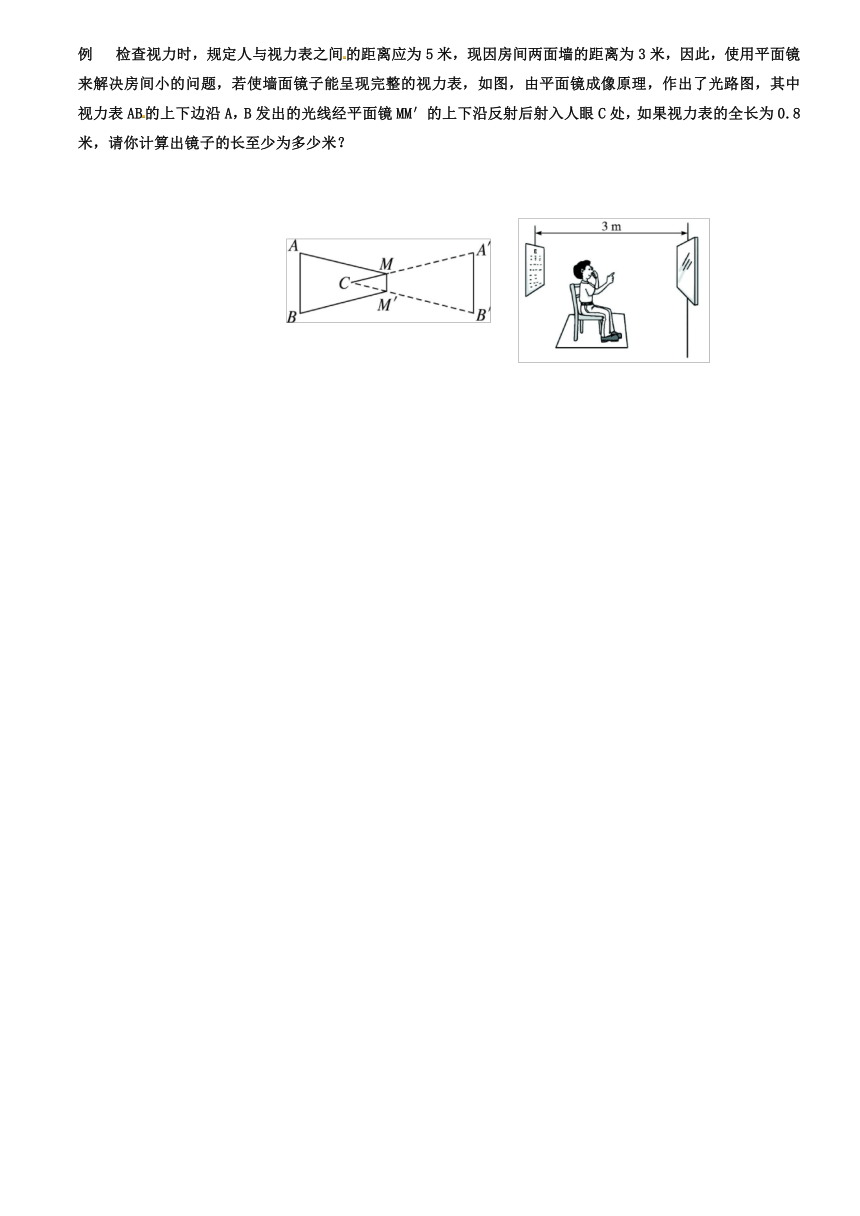
例 检查视力时,规定人与视力表之间的距离应为5米,现因房间两面墙的距离为3米,因此,使用平面镜来解决房间小的问题,若使墙面镜子能呈现完整的视力表,如图,由平面镜成像原理,作出了光路图,其中视力表AB的上下边沿A,B发出的光线经平面镜MM′的上下沿反射后射入人眼C处,如果视力表的全长为0.8米,请你计算出镜子的长至少为多少米?
3876675-190501834515162560
四、题组训练: 【师生活动】 学生独立完成后小组交流答案,教师在巡视过程中帮助有困难的学生
3900170594995【A组】1、如图,花丛中有一根路灯杆AB.在灯光下,乐乐在D点处的影长DE=3米,沿BD方向行走到达G点,DG=5米,这时乐乐的影长GH=5米.如果乐乐的身高为1.7米,求路灯杆AB的高度(精确到0.1米).
【B组】
40093906927852、如图,小刚在晚上由灯柱AE走向灯柱BC,当他走到M点时,发觉他身后影子的顶部刚好接触到灯柱AE的底部,当他向前再走12米到N点时,发觉他身前的影子刚好接触到灯柱BC的底部,已知小刚的身高是1.6米,两根灯柱的高度都是9.6米,设AM=NB=x米.求:两根灯柱之间的距离.
【C组】
3.如图所示,要测量电线杆AB的高度,发现电线杆的影子恰好落在土坡的坡面CD和地面BC上,量得CD=4 m,BC=10 m,CD与地面成30°角,且此时测得1 m杆的影子长为2 m,则电线杆的高度为多少米?
4419600142240
课堂小结:
达标检测:
教后反思:
安全教育:
一:知识链接:
50 2、8 3、900 120 4、C
二、新知探究
∵CD⊥FB,AB⊥FB,
∴CD∥AB
∴△CGE∽△AHE
∴CG/AH=EG/EH
即:CD?EF/AH=FD/FD+BD,
∴3?1.6/AH=2/2+15,
解得:AH=11.9
∴AB=AH+HB=AH+EF=11.9+1.6=13.5(m).
故答案为:13.5.
三、典例分析
作CD⊥MM′,垂足为D,并延长交A′B′于E,
∵AB∥MM′∥A′B′,
∴CE⊥A′B′,
∴△CMM′∽△CA′B′,
∴MM′A′B′=CDCE,
又∵CD=CE?DE=5?3=2,CE=5,A′B′=AB=0.8,
∴MM′0.8=25,
∴MM′=0.32(米),
∴镜长至少为0.32米。
四、题组训练
A组:根据题意得:AB⊥BH,CD⊥BH,FG⊥BH,(1分)
在Rt△ABE和Rt△CDE中,
∵AB⊥BH,CD⊥BH,
∴CD∥AB,
可证得:
△CDE∽△ABE
∴CDAB=DEDE+BD①,(4分)
同理:FGAB=HGHG+GD+BD②,(5分)
又CD=FG=1.7m,
由①、②可得:
DEDE+BD=HGHG+GD+BD,
即33+BD=510+BD,
解之得:BD=7.5m,(6分)
将BD=7.5代入①得:
AB=5.95m≈6.0m.(7分)
答:路灯杆AB的高度约为6.0m.(8分)
B组:∵MF∥BC,
∴△AMF∽△ABC
∴FM/BC=AM/AB,
∴1.6/9.6=x/2x+12
∴x=3
经检验x=3是原方程的根,并且符合题意。
∴AB=2x+12=2×3+12=18(m).
答:两个路灯之间的距离为18米。
C组
如图,过D作的延长线于E,连接并延长交的延长线于F,
米,与地面成角,
米,根据勾股定理得,米,
1米杆的影长为2米,
,
米,
米,
,
米。
答:电线杆的高度为。
课题: 25.6相似三角形的应用 备课人: 编制日期:
使用日期: 学科组长签字: 分管领导签字:
学习目标:1.经历对实际问题的探索,会利用相似三角形的性质测量物体的高度或距离.
2.在具体情境中建立数学模型,并综合运用数学知识解决简单实际问题.
一、知识链接:【师生活动】 学生独立思考回答,教师规范书写.
1.要测量不可直接到达的A、B两点距离,在O点设柱,取OA中点C,取OB中点D,测得CD=25m,则AB= 。
2.铁道栏杆短臂长1米,长臂长16米,当短臂端点下降0.5米,长臂升高 米。
3、在比例尺为1:3000的地图上,一个三角形的周长是4cm,面积为1cm2,则它的实际面积为 m2, 它的实际周长为 m。
4、如图,在直角梯形ABCD中,DC∥AB,∠DAB=90°,AC⊥BC,AC=BC,∠ABC的平分线分别交AD、AC于点E,F,则的值是( )
A.
1134110263525C
D
A
B
C
D
A
B
-1270309880D
C
O
A
B
D
C
O
A
B
B.
C.
67945326390
D.
二、新知探究:【师生活动】学生自主学习、独立思考后,小组合作交流,学生展示后教师点评归纳,.
42710103778251、如图,九年级(1)班课外活动小组利用标杆测量学校旗杆的高度,已知标杆高度CD=3m,标杆与旗杆的水平距离BD=15m,人的眼睛与地面的高度EF=1.6m,人与标杆CD的水平距离DF=2m,求旗杆AB的高度.
三、典例分析:【师生活动】 学生独立思考后,小组合作交流,教师对有困难的学生进行指导,小组代表展示,教师点评过程中强调易错点.
例 检查视力时,规定人与视力表之间的距离应为5米,现因房间两面墙的距离为3米,因此,使用平面镜来解决房间小的问题,若使墙面镜子能呈现完整的视力表,如图,由平面镜成像原理,作出了光路图,其中视力表AB的上下边沿A,B发出的光线经平面镜MM′的上下沿反射后射入人眼C处,如果视力表的全长为0.8米,请你计算出镜子的长至少为多少米?
3876675-190501834515162560
四、题组训练: 【师生活动】 学生独立完成后小组交流答案,教师在巡视过程中帮助有困难的学生
3900170594995【A组】1、如图,花丛中有一根路灯杆AB.在灯光下,乐乐在D点处的影长DE=3米,沿BD方向行走到达G点,DG=5米,这时乐乐的影长GH=5米.如果乐乐的身高为1.7米,求路灯杆AB的高度(精确到0.1米).
【B组】
40093906927852、如图,小刚在晚上由灯柱AE走向灯柱BC,当他走到M点时,发觉他身后影子的顶部刚好接触到灯柱AE的底部,当他向前再走12米到N点时,发觉他身前的影子刚好接触到灯柱BC的底部,已知小刚的身高是1.6米,两根灯柱的高度都是9.6米,设AM=NB=x米.求:两根灯柱之间的距离.
【C组】
3.如图所示,要测量电线杆AB的高度,发现电线杆的影子恰好落在土坡的坡面CD和地面BC上,量得CD=4 m,BC=10 m,CD与地面成30°角,且此时测得1 m杆的影子长为2 m,则电线杆的高度为多少米?
4419600142240
课堂小结:
达标检测:
教后反思:
安全教育:
一:知识链接:
50 2、8 3、900 120 4、C
二、新知探究
∵CD⊥FB,AB⊥FB,
∴CD∥AB
∴△CGE∽△AHE
∴CG/AH=EG/EH
即:CD?EF/AH=FD/FD+BD,
∴3?1.6/AH=2/2+15,
解得:AH=11.9
∴AB=AH+HB=AH+EF=11.9+1.6=13.5(m).
故答案为:13.5.
三、典例分析
作CD⊥MM′,垂足为D,并延长交A′B′于E,
∵AB∥MM′∥A′B′,
∴CE⊥A′B′,
∴△CMM′∽△CA′B′,
∴MM′A′B′=CDCE,
又∵CD=CE?DE=5?3=2,CE=5,A′B′=AB=0.8,
∴MM′0.8=25,
∴MM′=0.32(米),
∴镜长至少为0.32米。
四、题组训练
A组:根据题意得:AB⊥BH,CD⊥BH,FG⊥BH,(1分)
在Rt△ABE和Rt△CDE中,
∵AB⊥BH,CD⊥BH,
∴CD∥AB,
可证得:
△CDE∽△ABE
∴CDAB=DEDE+BD①,(4分)
同理:FGAB=HGHG+GD+BD②,(5分)
又CD=FG=1.7m,
由①、②可得:
DEDE+BD=HGHG+GD+BD,
即33+BD=510+BD,
解之得:BD=7.5m,(6分)
将BD=7.5代入①得:
AB=5.95m≈6.0m.(7分)
答:路灯杆AB的高度约为6.0m.(8分)
B组:∵MF∥BC,
∴△AMF∽△ABC
∴FM/BC=AM/AB,
∴1.6/9.6=x/2x+12
∴x=3
经检验x=3是原方程的根,并且符合题意。
∴AB=2x+12=2×3+12=18(m).
答:两个路灯之间的距离为18米。
C组
如图,过D作的延长线于E,连接并延长交的延长线于F,
米,与地面成角,
米,根据勾股定理得,米,
1米杆的影长为2米,
,
米,
米,
,
米。
答:电线杆的高度为。
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
