山东省济南市长清第一中学2020-2021学年高一上学期12月第三次月考数学试题 Word版含答案
文档属性
| 名称 | 山东省济南市长清第一中学2020-2021学年高一上学期12月第三次月考数学试题 Word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 295.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-04 16:47:58 | ||
图片预览




文档简介
长清第一中学2020-2021学年第一学期第三次质量检测
数学试题 时间120分钟
一 单选题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.把-1 485°化成k·360°+α(0°≤α<360°,k∈Z)的形式是( )
A.315°-5×360° B.45°-4×360°
C.-315°-4×360° D.-45°-10×180°
2.下列转化结果错误的是( )
A.60化成弧度是false B.-150化成弧度是-false
C.-false化成度是-600D.false化成度是15
3.如图所示,角的终边与单位圆交于点Pfalse,则cos(-)的值为( )
A.-false B.-false C.false D.false
4.如图所示,函数y=cos x|tan x|false的图象是( )
5.在[0,2]内,不等式sin x<-false的解集是( )
A.(0,) B.false C.false D.false
6.根据表格中的数据,可以判断方程ex-x-2=0必有一个根在区间( )
x
-1
0
1
2
3
ex
0.37
1
2.78
7.39
20.09
x+2
1
2
3
4
5
A.(-1,0) B.(0,1) C.(1,2) D.(2,3)
7.已知sin +cos =false,∈(0,),则tan 的值是( )
A.false B.-false C.false D.-false
8.若函数f(x)=x3+x2-2x-2的一个零点(正数)附近的函数值用二分法逐次计算,参考数据如下表:
f(1)=-2
f(1.5)=0.625
f(1.25)≈-0.984
f(1.375)≈-0.260
f(1.437 5)≈0.162
f(1.406 25)≈-0.054
那么方程x3+x2-2x-2=0的一个近似解(精确度0.04)为( )
A.1.5 B.1.25 C.1.375 D.1.437 5
二 多选题(本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分.)
9.下列表示中正确的是( )
A.终边在x轴上的角的集合是{|=k,k∈Z}
B.终边在y轴上的角的集合是false
C.终边在坐标轴上的角的集合是false
D.终边在直线y=x上的角的集合是false
10.对于正弦函数y=sin x的图象,下列说法正确的是( )
A.向左右无限伸展 B.与y=cos x的图象形状相同,只是位置不同
C.与x轴有无数个交点 D.关于y轴对称
11.在△ABC中,给出下列四个式子,其中为常数的是( )
A sin(A+B)+sin C; B. cos(A+B)+cos C;
C sin(2A+2B)+sin 2C; D.cos(2A+2B)+cos 2C.
12. 关于三角函数的图象,有下列命题,其中正确命题的序号是( )
A y=sin |x|与y=sin x的图象关于y轴对称;
B y=cos(-x)与y=cos |x|的图象相同;
C y=|sin x|与y=sin(-x)的图象关于x轴对称;
D y=cos x与y=cos(-x)的图象关于y轴对称.
三 填空题:本题共4小题,每小题5分,共20分.把答案填在答题卡中的横线上.
13.tan 405-sin 450+cos 750=________.
14.若为第三象限角,则false+false的值为 .
15.计算sin21+sin22+…+sin288+sin289=________.
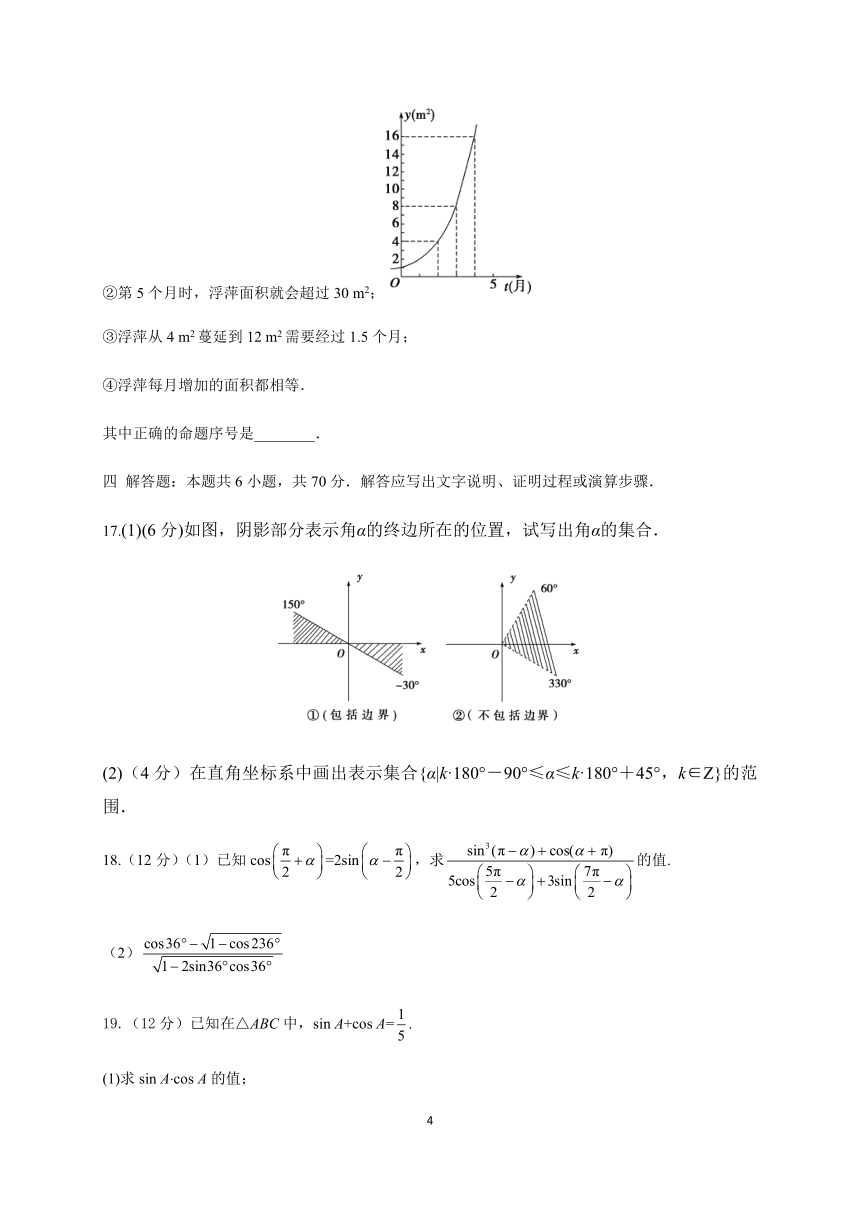
16.如图所示,某池塘中浮萍蔓延的面积y(m2)与时间t(月)的关系y=at,有以下几种说法:
①这个指数函数的底数为2;
②第5个月时,浮萍面积就会超过30 m2;
③浮萍从4 m2蔓延到12 m2需要经过1.5个月;
④浮萍每月增加的面积都相等.
其中正确的命题序号是________.
四 解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(1)(6分)如图,阴影部分表示角α的终边所在的位置,试写出角α的集合.
(2)(4分)在直角坐标系中画出表示集合{α|k·180°-90°≤α≤k·180°+45°,k∈Z}的范围.
18.(12分)(1)已知cosfalse=2sinfalse,求false的值.
(2)false
19.(12分)已知在△ABC中,sin A+cos A=false.
(1)求sin Acos A的值;
(2)判断△ABC是锐角三角形还是钝角三角形;
(3)求tan A的值.
20.(12分)函数f(x)=Asin false+1(A>0,>0)的最大值为3,其图象相邻两条对称轴之间的距离为false.
(1)求函数f(x)的解析式;
(2)设∈false,ffalse=2,求的值.
21.(12分)设函数f(x)=falsesinfalse,x∈R.
(1)求函数f(x)的最小正周期和单调递增区间;
(2)求函数f(x)在区间false上的最小值和最大值,并求出取最值时x的值.
22.(12分)今年冬季,我国大部分地区遭遇雾霾天气,给人们的健康、交通安全等带来了严重影响.经研究,发现工业废气等污染物排放是雾霾形成和持续的重要因素,污染治理刻不容缓.为此,某工厂新购置并安装了先进的废气处理设备,使产生的废气经过过滤后排放,以降低对空气的污染.已知过滤过程中废气的污染物数量P(单位:mg/L)与过滤时间t(单位:小时)间的关系为P=P0e-kt (P0,k均为非零常数,e为自然对数的底数),其中P0为t=0时的污染物数量.若经过5小时过滤后还剩余90%的污染物.
(1)求常数k的值;
(2)试计算污染物减少到40%至少需要多少时间(精确到1小时,参考数据:ln 0.2≈-1.61,ln 0.3≈-1.20,ln 0.4≈-0.92,ln 0.5≈-0.69,ln 0.9≈-0.11.)
月考答案
A 2. C 3. B 4.C 5. C 6.C 7.D 8.D
ABC 10. ABC 11. BC 12. BD
false 14 . - 3 15. false 16. ①②
17.(1)①{α|-30°+k·360°≤α≤k·360°,k∈Z}∪{α|150°+k·360°≤α≤180°+k·360°,k∈Z}={α|-30°+k·180°≤α≤k·180°,k∈Z};
②{α|-30°+k·360°<α<60°+k·360°,k∈Z}.
(2)
18.(1)∵cosfalse=2sinfalse,∴-sin =-2sinfalse,∴sin =2cos ,即tan =2.
∴false=false.
=false=false=false
=false=false=false
=false=false=false=false.
(2)(1)原式=false
=false=false=false=1.
19.(1)由sin A+cos A=false,
两边平方,得1+2sin Acos A=false,
所以sin Acos A=-false.
(2)由(1)得sin Acos A=-false<0.
又0 所以A为钝角.所以△ABC是钝角三角形.
(3)因为sin Acos A=-false,
所以(sin A-cos A)2=1-2sin Acos A=1+false=false,
又sin A>0,cos A<0,
所以sin A-cos A>0,
所以sin A-cos A=false.
又sin A+cos A=false,
所以sin A=false,cos A=-false.
所以tan A=false=false=-false.
20.(1)因为函数f(x)的最大值为3,所以A+1=3,即A=2.因为函数图象的相邻两条对称轴之间的距离为false,所以最小正周期T=,所以=2,故函数f(x)的解析式为
y=2sin false+1.
(2)因为f false=2sin false+1=2,
即sin false=false,
又因为0< 所以-false=false,故=false.
21.(1)最小正周期T=false=,
由2k-false≤2x-false≤2k+false(k∈Z),
得k-false≤x≤k+false(k∈Z),
∴函数f(x)的单调递增区间是false(k∈Z).
(2)令t=2x-false,则由false≤x≤false可得0≤t≤false,
∴当t=false,即x=false时,ymin=falsefalse=-1,
∴当t=false,即x=false时,ymax=false1=false.
22.(1)由已知,当t=0时,P=P0;
当t=5时,P=90%P0.
于是有90%P0=P0e-5k.
解得k=-falseln 0.9(或0.022).
(2)由(1)得,P=false.
当P=40%P0时,有0.4P0=false.
解得t=false≈false=false≈41.82.
故污染物减少到40%至少需要42小时.
数学试题 时间120分钟
一 单选题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.把-1 485°化成k·360°+α(0°≤α<360°,k∈Z)的形式是( )
A.315°-5×360° B.45°-4×360°
C.-315°-4×360° D.-45°-10×180°
2.下列转化结果错误的是( )
A.60化成弧度是false B.-150化成弧度是-false
C.-false化成度是-600D.false化成度是15
3.如图所示,角的终边与单位圆交于点Pfalse,则cos(-)的值为( )
A.-false B.-false C.false D.false
4.如图所示,函数y=cos x|tan x|false的图象是( )
5.在[0,2]内,不等式sin x<-false的解集是( )
A.(0,) B.false C.false D.false
6.根据表格中的数据,可以判断方程ex-x-2=0必有一个根在区间( )
x
-1
0
1
2
3
ex
0.37
1
2.78
7.39
20.09
x+2
1
2
3
4
5
A.(-1,0) B.(0,1) C.(1,2) D.(2,3)
7.已知sin +cos =false,∈(0,),则tan 的值是( )
A.false B.-false C.false D.-false
8.若函数f(x)=x3+x2-2x-2的一个零点(正数)附近的函数值用二分法逐次计算,参考数据如下表:
f(1)=-2
f(1.5)=0.625
f(1.25)≈-0.984
f(1.375)≈-0.260
f(1.437 5)≈0.162
f(1.406 25)≈-0.054
那么方程x3+x2-2x-2=0的一个近似解(精确度0.04)为( )
A.1.5 B.1.25 C.1.375 D.1.437 5
二 多选题(本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分.)
9.下列表示中正确的是( )
A.终边在x轴上的角的集合是{|=k,k∈Z}
B.终边在y轴上的角的集合是false
C.终边在坐标轴上的角的集合是false
D.终边在直线y=x上的角的集合是false
10.对于正弦函数y=sin x的图象,下列说法正确的是( )
A.向左右无限伸展 B.与y=cos x的图象形状相同,只是位置不同
C.与x轴有无数个交点 D.关于y轴对称
11.在△ABC中,给出下列四个式子,其中为常数的是( )
A sin(A+B)+sin C; B. cos(A+B)+cos C;
C sin(2A+2B)+sin 2C; D.cos(2A+2B)+cos 2C.
12. 关于三角函数的图象,有下列命题,其中正确命题的序号是( )
A y=sin |x|与y=sin x的图象关于y轴对称;
B y=cos(-x)与y=cos |x|的图象相同;
C y=|sin x|与y=sin(-x)的图象关于x轴对称;
D y=cos x与y=cos(-x)的图象关于y轴对称.
三 填空题:本题共4小题,每小题5分,共20分.把答案填在答题卡中的横线上.
13.tan 405-sin 450+cos 750=________.
14.若为第三象限角,则false+false的值为 .
15.计算sin21+sin22+…+sin288+sin289=________.
16.如图所示,某池塘中浮萍蔓延的面积y(m2)与时间t(月)的关系y=at,有以下几种说法:
①这个指数函数的底数为2;
②第5个月时,浮萍面积就会超过30 m2;
③浮萍从4 m2蔓延到12 m2需要经过1.5个月;
④浮萍每月增加的面积都相等.
其中正确的命题序号是________.
四 解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(1)(6分)如图,阴影部分表示角α的终边所在的位置,试写出角α的集合.
(2)(4分)在直角坐标系中画出表示集合{α|k·180°-90°≤α≤k·180°+45°,k∈Z}的范围.
18.(12分)(1)已知cosfalse=2sinfalse,求false的值.
(2)false
19.(12分)已知在△ABC中,sin A+cos A=false.
(1)求sin Acos A的值;
(2)判断△ABC是锐角三角形还是钝角三角形;
(3)求tan A的值.
20.(12分)函数f(x)=Asin false+1(A>0,>0)的最大值为3,其图象相邻两条对称轴之间的距离为false.
(1)求函数f(x)的解析式;
(2)设∈false,ffalse=2,求的值.
21.(12分)设函数f(x)=falsesinfalse,x∈R.
(1)求函数f(x)的最小正周期和单调递增区间;
(2)求函数f(x)在区间false上的最小值和最大值,并求出取最值时x的值.
22.(12分)今年冬季,我国大部分地区遭遇雾霾天气,给人们的健康、交通安全等带来了严重影响.经研究,发现工业废气等污染物排放是雾霾形成和持续的重要因素,污染治理刻不容缓.为此,某工厂新购置并安装了先进的废气处理设备,使产生的废气经过过滤后排放,以降低对空气的污染.已知过滤过程中废气的污染物数量P(单位:mg/L)与过滤时间t(单位:小时)间的关系为P=P0e-kt (P0,k均为非零常数,e为自然对数的底数),其中P0为t=0时的污染物数量.若经过5小时过滤后还剩余90%的污染物.
(1)求常数k的值;
(2)试计算污染物减少到40%至少需要多少时间(精确到1小时,参考数据:ln 0.2≈-1.61,ln 0.3≈-1.20,ln 0.4≈-0.92,ln 0.5≈-0.69,ln 0.9≈-0.11.)
月考答案
A 2. C 3. B 4.C 5. C 6.C 7.D 8.D
ABC 10. ABC 11. BC 12. BD
false 14 . - 3 15. false 16. ①②
17.(1)①{α|-30°+k·360°≤α≤k·360°,k∈Z}∪{α|150°+k·360°≤α≤180°+k·360°,k∈Z}={α|-30°+k·180°≤α≤k·180°,k∈Z};
②{α|-30°+k·360°<α<60°+k·360°,k∈Z}.
(2)
18.(1)∵cosfalse=2sinfalse,∴-sin =-2sinfalse,∴sin =2cos ,即tan =2.
∴false=false.
=false=false=false
=false=false=false
=false=false=false=false.
(2)(1)原式=false
=false=false=false=1.
19.(1)由sin A+cos A=false,
两边平方,得1+2sin Acos A=false,
所以sin Acos A=-false.
(2)由(1)得sin Acos A=-false<0.
又0
(3)因为sin Acos A=-false,
所以(sin A-cos A)2=1-2sin Acos A=1+false=false,
又sin A>0,cos A<0,
所以sin A-cos A>0,
所以sin A-cos A=false.
又sin A+cos A=false,
所以sin A=false,cos A=-false.
所以tan A=false=false=-false.
20.(1)因为函数f(x)的最大值为3,所以A+1=3,即A=2.因为函数图象的相邻两条对称轴之间的距离为false,所以最小正周期T=,所以=2,故函数f(x)的解析式为
y=2sin false+1.
(2)因为f false=2sin false+1=2,
即sin false=false,
又因为0<
21.(1)最小正周期T=false=,
由2k-false≤2x-false≤2k+false(k∈Z),
得k-false≤x≤k+false(k∈Z),
∴函数f(x)的单调递增区间是false(k∈Z).
(2)令t=2x-false,则由false≤x≤false可得0≤t≤false,
∴当t=false,即x=false时,ymin=falsefalse=-1,
∴当t=false,即x=false时,ymax=false1=false.
22.(1)由已知,当t=0时,P=P0;
当t=5时,P=90%P0.
于是有90%P0=P0e-5k.
解得k=-falseln 0.9(或0.022).
(2)由(1)得,P=false.
当P=40%P0时,有0.4P0=false.
解得t=false≈false=false≈41.82.
故污染物减少到40%至少需要42小时.
同课章节目录
