2011年11月安徽优质课大赛课件 方程的根与函数的零点 马鞍山市红星中学 何玉宝
文档属性
| 名称 | 2011年11月安徽优质课大赛课件 方程的根与函数的零点 马鞍山市红星中学 何玉宝 |  | |
| 格式 | rar | ||
| 文件大小 | 172.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-11-23 16:18:53 | ||
图片预览




文档简介
(共16张PPT)
方程的根与函数的零点
马鞍山市红星中学 何玉宝
方程解法史话
在人类用智慧架设的无数座从未知通向已知的金桥中,方程的求解是其中璀璨的一座,虽然今天我们可以从教科书中了解各式各样方程的解法,但这一切却经历了相当漫长的岁月. 我国古代数学家已比较系统地解决了部分方程的求解的问题。如约公元50年—100年编成的《九章算术》,就给出了求一次方程、二次方程和三次方程根的具体方法…
方程实例求解
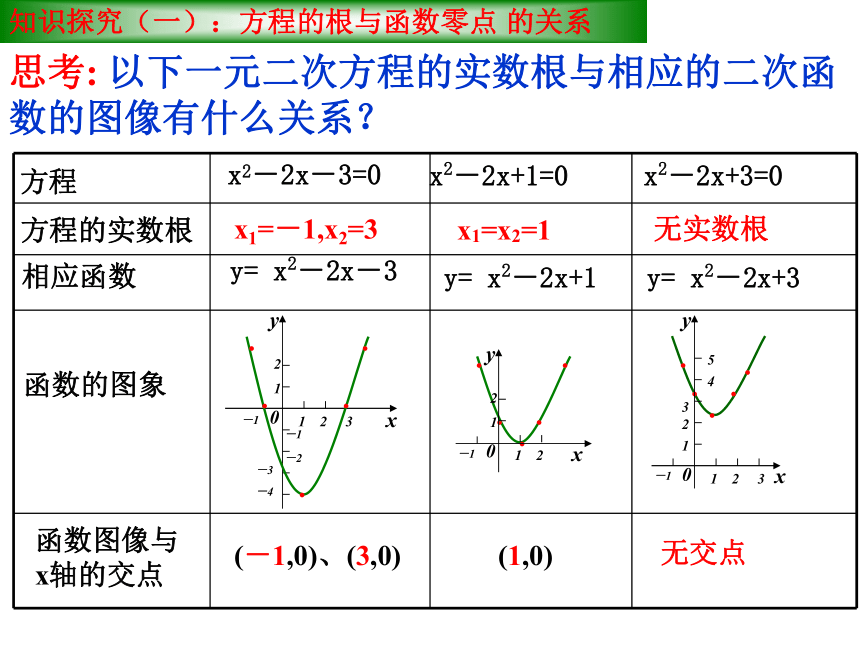
方程
x2-2x+1=0
x2-2x+3=0
y= x2-2x-3
相应函数
函数的图象
方程的实数根
x1=-1,x2=3
x1=x2=1
无实数根
(-1,0)、(3,0)
(1,0)
无交点
x2-2x-3=0
x
y
0
-1
3
2
1
1
2
-1
-2
-3
-4
.
.
.
.
.
.
.
.
.
.
x
y
0
-1
3
2
1
1
2
5
4
3
y= x2-2x+1
.
.
.
.
.
y
x
0
-1
2
1
1
2
y= x2-2x+3
思考: 以下一元二次方程的实数根与相应的二次函数的图像有什么关系?
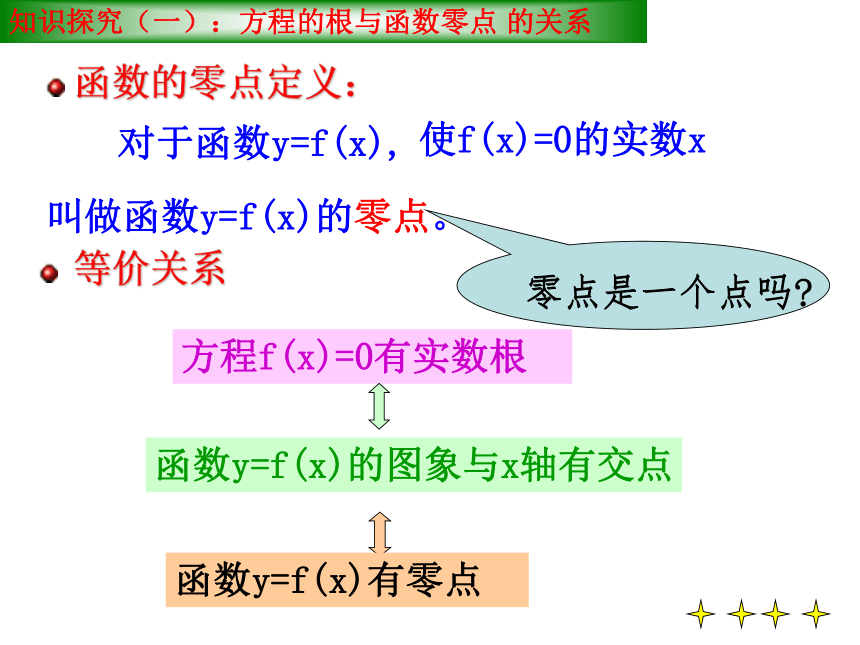
知识探究(一):方程的根与函数零点 的关系
函数图像与
x轴的交点
方程f(x)=0有实数根
函数y=f(x)的图象与x轴有交点
函数y=f(x)有零点
对于函数y=f(x),
叫做函数y=f(x)的零点。
函数的零点定义:
等价关系
使f(x)=0的实数x
知识探究(一):方程的根与函数零点 的关系
零点是一个点吗
1、函数y=x2-5x+6的零点是( )
A(3,0),(2,0); B x=2 ;
C x=3 ; D 2和3.
即兴练习
D
B
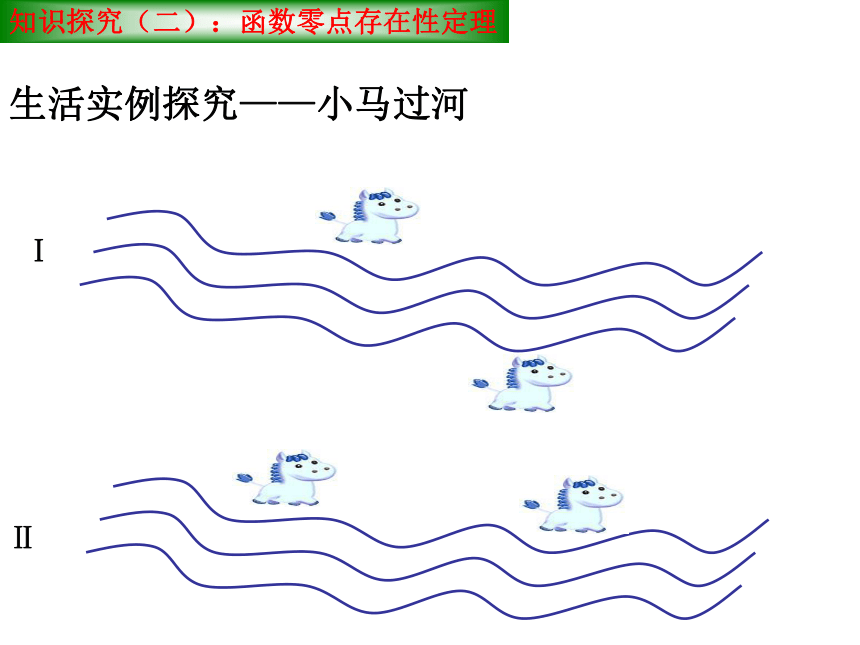
Ⅰ
Ⅱ
生活实例探究——小马过河
知识探究(二):函数零点存在性定理
<
<
知识探究(二):函数零点存在性定理
知识探究(二):函数零点存在性定理
函数零点存在性定理:
函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a) f(b)<0,那么,函数y=f(x)在区间(a,b)内有零点,即存在c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0 的根.
1 上述定理中,函数的零点是否唯一?
思考:
2 若 ,则函数在区间(a,b)内一定没有零点吗?
例1 观察下表,分析函数
在定义域内是否存在零点?
x -2 -1 0 1 2
f(x) -109 -10 -1 8 107
由上表和右图可知
f(2)<0,f(3)>0,
即f(2)·f(3)<0,
说明这个函数在区间(2,3)内
有零点。
由于函数f(x)在定义域
(0,+∞)内是增函数,所以
它仅有一个零点。
解法1:用计算器或计算机作出x、f(x)的对应值表
和图象
-4
-1.3069
1.0986
3.3863
5.6094
7.7918
9.9459
12.0794
14.1972
1
2
3
4
5
6
7
8
9
x
f(x)
.
.
.
.
.
.
.
.
.
x
0
-2
-4
-6
10
5
y
2
4
10
8
6
12
14
8
7
6
4
3
2
1
9
的零点个数
例2 求函数
6
2
ln
)
(
-
+
=
x
x
x
f
一题多解
的零点个数
例2 求函数
6
2
ln
)
(
-
+
=
x
x
x
f
0
1
2
3
4
5
-1
-2
1
2
3
4
5
-1
-2
x
y
6
1、对于定义在R上的连续函数y=f(x),若 f(a).f(b)<0 (a,b R,且a在(a,b)内( )
A 只有一个零点 B 至少有一个零点
C 无零点 D 无法确定有无零点
B
知识巩固练习:
3、若函数 有3个零点
则
2、若方程 在(0,1)内有一解,
则 的取值范围是____________;
小结:
1、函数y=f(x)的零点的定义
2、等价关系
3、函数y=f(x)的零点存在性的判定
使f(x)=0的实数x叫做函数y=f(x)的零点
方程f(x)=0
有实根
函数y=f(x)的图象与x轴有交点
函数y=f(x)有零点
知识总结:
课后作业:
1
.教材
P
9
2
习题
3
.
1
(
A
组)第
2
题;
2.
3.
课后延展:
的零点在(2,3)内
已知函数
6
2
ln
)
(
-
+
=
x
x
x
f
如何求这个零点的近似值?
谢 谢 指 导!
方程的根与函数的零点
马鞍山市红星中学 何玉宝
方程解法史话
在人类用智慧架设的无数座从未知通向已知的金桥中,方程的求解是其中璀璨的一座,虽然今天我们可以从教科书中了解各式各样方程的解法,但这一切却经历了相当漫长的岁月. 我国古代数学家已比较系统地解决了部分方程的求解的问题。如约公元50年—100年编成的《九章算术》,就给出了求一次方程、二次方程和三次方程根的具体方法…
方程实例求解
方程
x2-2x+1=0
x2-2x+3=0
y= x2-2x-3
相应函数
函数的图象
方程的实数根
x1=-1,x2=3
x1=x2=1
无实数根
(-1,0)、(3,0)
(1,0)
无交点
x2-2x-3=0
x
y
0
-1
3
2
1
1
2
-1
-2
-3
-4
.
.
.
.
.
.
.
.
.
.
x
y
0
-1
3
2
1
1
2
5
4
3
y= x2-2x+1
.
.
.
.
.
y
x
0
-1
2
1
1
2
y= x2-2x+3
思考: 以下一元二次方程的实数根与相应的二次函数的图像有什么关系?
知识探究(一):方程的根与函数零点 的关系
函数图像与
x轴的交点
方程f(x)=0有实数根
函数y=f(x)的图象与x轴有交点
函数y=f(x)有零点
对于函数y=f(x),
叫做函数y=f(x)的零点。
函数的零点定义:
等价关系
使f(x)=0的实数x
知识探究(一):方程的根与函数零点 的关系
零点是一个点吗
1、函数y=x2-5x+6的零点是( )
A(3,0),(2,0); B x=2 ;
C x=3 ; D 2和3.
即兴练习
D
B
Ⅰ
Ⅱ
生活实例探究——小马过河
知识探究(二):函数零点存在性定理
<
<
知识探究(二):函数零点存在性定理
知识探究(二):函数零点存在性定理
函数零点存在性定理:
函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a) f(b)<0,那么,函数y=f(x)在区间(a,b)内有零点,即存在c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0 的根.
1 上述定理中,函数的零点是否唯一?
思考:
2 若 ,则函数在区间(a,b)内一定没有零点吗?
例1 观察下表,分析函数
在定义域内是否存在零点?
x -2 -1 0 1 2
f(x) -109 -10 -1 8 107
由上表和右图可知
f(2)<0,f(3)>0,
即f(2)·f(3)<0,
说明这个函数在区间(2,3)内
有零点。
由于函数f(x)在定义域
(0,+∞)内是增函数,所以
它仅有一个零点。
解法1:用计算器或计算机作出x、f(x)的对应值表
和图象
-4
-1.3069
1.0986
3.3863
5.6094
7.7918
9.9459
12.0794
14.1972
1
2
3
4
5
6
7
8
9
x
f(x)
.
.
.
.
.
.
.
.
.
x
0
-2
-4
-6
10
5
y
2
4
10
8
6
12
14
8
7
6
4
3
2
1
9
的零点个数
例2 求函数
6
2
ln
)
(
-
+
=
x
x
x
f
一题多解
的零点个数
例2 求函数
6
2
ln
)
(
-
+
=
x
x
x
f
0
1
2
3
4
5
-1
-2
1
2
3
4
5
-1
-2
x
y
6
1、对于定义在R上的连续函数y=f(x),若 f(a).f(b)<0 (a,b R,且a
A 只有一个零点 B 至少有一个零点
C 无零点 D 无法确定有无零点
B
知识巩固练习:
3、若函数 有3个零点
则
2、若方程 在(0,1)内有一解,
则 的取值范围是____________;
小结:
1、函数y=f(x)的零点的定义
2、等价关系
3、函数y=f(x)的零点存在性的判定
使f(x)=0的实数x叫做函数y=f(x)的零点
方程f(x)=0
有实根
函数y=f(x)的图象与x轴有交点
函数y=f(x)有零点
知识总结:
课后作业:
1
.教材
P
9
2
习题
3
.
1
(
A
组)第
2
题;
2.
3.
课后延展:
的零点在(2,3)内
已知函数
6
2
ln
)
(
-
+
=
x
x
x
f
如何求这个零点的近似值?
谢 谢 指 导!
