2011年11月安徽优质课大赛课件 二分法 黄山市歙县中学 姜林峰
文档属性
| 名称 | 2011年11月安徽优质课大赛课件 二分法 黄山市歙县中学 姜林峰 |

|
|
| 格式 | rar | ||
| 文件大小 | 293.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-11-23 16:21:24 | ||
图片预览





文档简介
(共16张PPT)
§3.1.2 用二分法求方程的近似解
黄山市歙县中学 姜林峰
新课引入
某个雷电交加的夜晚,医院的医生正在抢救一个危重病人,忽然电停了,医院采取了应急措施。据了解原因是供电站到医院的某处线路出现了故障,维修工如何迅速查出故障所在 (线路长10km,每50m一棵电线杆)
如果沿着线路一小段一小段查找,困难很多。每查一个点要爬一次电线杆子,10km长,大约有200根电线杆子。
维修线路的工人师傅怎样工作合理?
想一想
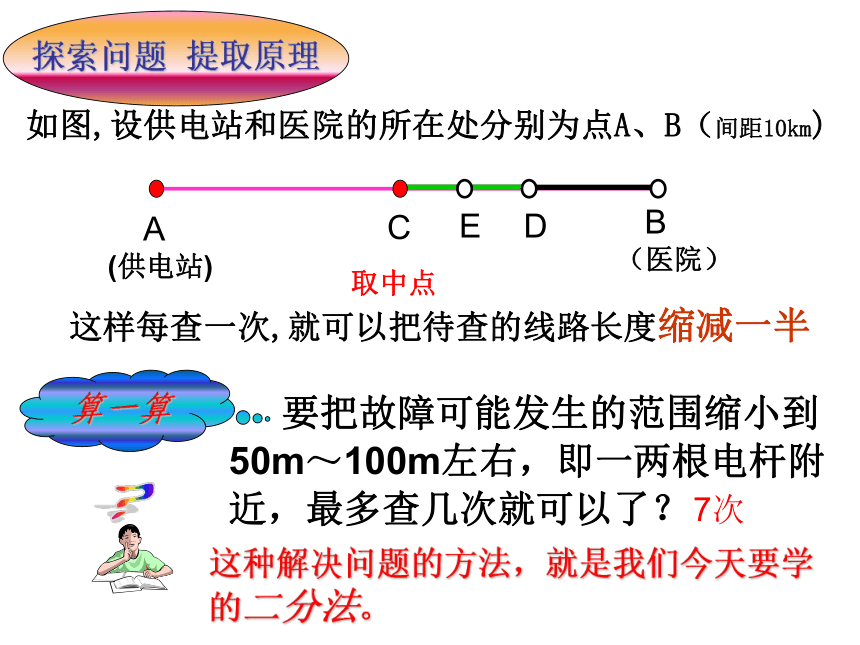
探索问题 提取原理
如图,设供电站和医院的所在处分别为点A、B(间距10km)
A
(供电站)
这样每查一次,就可以把待查的线路长度缩减一半
C
B
(医院)
D
E
要把故障可能发生的范围缩小到50m~100m左右,即一两根电杆附近,最多查几次就可以了?
算一算
7次
取中点
这种解决问题的方法,就是我们今天要学的二分法。
§3.1.2 用二分法求方程的近似解
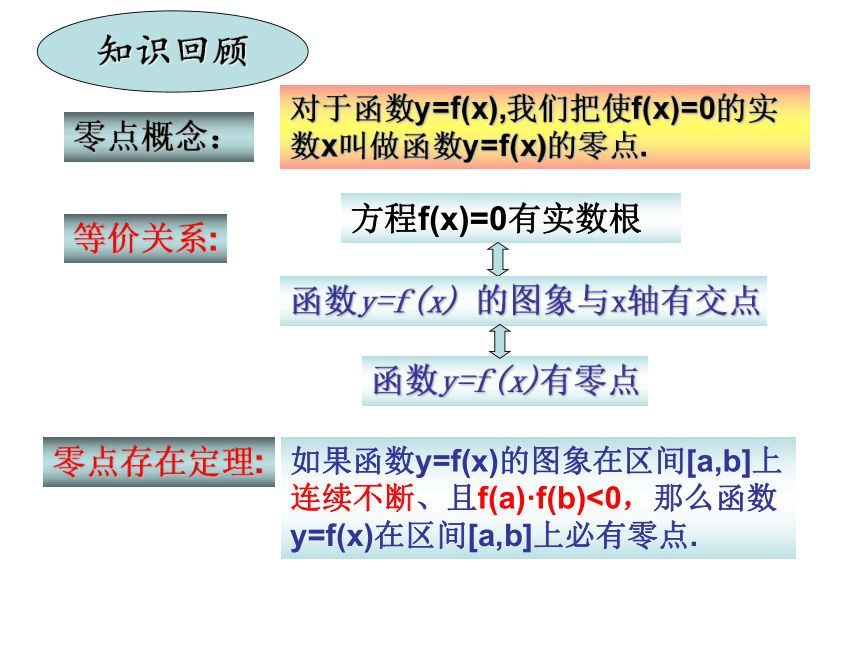
知识回顾
对于函数y=f(x),我们把使f(x)=0的实数x叫做函数y=f(x)的零点.
零点概念:
等价关系:
方程f(x)=0有实数根
函数y=f(x) 的图象与x轴有交点
函数y=f(x)有零点
零点存在定理:
如果函数y=f(x)的图象在区间[a,b]上连续不断、且f(a)·f(b)<0,那么函数y=f(x)在区间[a,b]上必有零点.
问题1:你能求下列方程的解吗?
新知探究
问题2:以方程 为例,能不能确定方程根的大概范围呢?
回顾旧知:
问题2:以方程 为例,能不能确定方程根的大概范围呢?
新知探究
2
3
2.5
2.75
问题3:你有进一步缩小函数零点的范围的方法吗?
2.625
新知探究
二分法的定义:
概念形成
二分法的理论依据是什么?
想一想?
次数 区间长度:
1
2
3
4
0.5
所以方程的近似解为:
2.5
-0.084
2.5
3
0.25
0.125
0.0625
2.75
0.512
2.625
0.215
0.066
2.5625
2.5
2.75
2
3
由于|2.5625-2.5|=0.0625<0.1
2.5
2.75
2.65
2.5625
问题4:
初始区间(2,3)
且
探究归纳
1.确定区间[a,b],验证f(a)·f(b)<0,给定精确度ε;
3.计算f(c);
2.求区间(a,b)的中点c;
(1)若f(c)=0,则c就是函数的零点;
(2)若f(a)· f(c)<0,则令b= c(此时零点x0∈(a, c) );
(3)若f(c)· f(b)<0,则令a= c(此时零点x0∈( c, b) ).
4.判断是否达到精确度ε:即若|a-b|<ε,则得到零点近似值a(或b);否则重复步骤2~4.
例1:
x
y
0
x
y
0
0
x
y
0
x
y
A
D
c
B
概念拓展 实践探究
实践探究
想一想
如何确定初始区间
解:
记函数
x
y
0
2
x
y
0
2
x
y
0
2
概念拓展 实践探究
解:设 =x,则建立函数f(x)=x3-3,求f(x)的零点的近似值。
例3.不用计算器,求 的近似值(精确度0.01)
取a=1,b=2,f(1)=-2<0,f(2)=5>0,
x1=1.5,f(x1)=0.375>0,区间[1,1.5],
x2=1.25,f(x2)=-0.0469<0,区间[1.25,1.5],
x3=1.375,f(x3)=0.5996>0,区间[1.25,1.375],
概念拓展 实践探究
x5=1.28125,f(x5)=0.1033>0,区间[1.25,1.28125],
x6=1.26562,f(x6)=0.0273,区间[1.25,1.26562],
x7=1.25781,f(x7)=-0.1,区间[1.25781,1.26562],
∴ 1.26.
x4=1.3125,f(x4)=0.2610,区间[1.25,1.3125]
周而复始怎么办
定区间,找中点,
零点落在异号间,
口 诀
反思小结 体会收获
中值计算两边看;
区间长度缩一半;
精确度上来判断.
巩固提高 课外练习
1、课堂作业:
P92习题3.1A组 3、 4、 5
2、课外作业:
(1)阅读课本P91 《中外历史上的方程求解》;
(2)12只金表中有一只份量略轻,如何用一架天平秤,在秤量次数最少的情况下分辩出来?
§3.1.2 用二分法求方程的近似解
黄山市歙县中学 姜林峰
新课引入
某个雷电交加的夜晚,医院的医生正在抢救一个危重病人,忽然电停了,医院采取了应急措施。据了解原因是供电站到医院的某处线路出现了故障,维修工如何迅速查出故障所在 (线路长10km,每50m一棵电线杆)
如果沿着线路一小段一小段查找,困难很多。每查一个点要爬一次电线杆子,10km长,大约有200根电线杆子。
维修线路的工人师傅怎样工作合理?
想一想
探索问题 提取原理
如图,设供电站和医院的所在处分别为点A、B(间距10km)
A
(供电站)
这样每查一次,就可以把待查的线路长度缩减一半
C
B
(医院)
D
E
要把故障可能发生的范围缩小到50m~100m左右,即一两根电杆附近,最多查几次就可以了?
算一算
7次
取中点
这种解决问题的方法,就是我们今天要学的二分法。
§3.1.2 用二分法求方程的近似解
知识回顾
对于函数y=f(x),我们把使f(x)=0的实数x叫做函数y=f(x)的零点.
零点概念:
等价关系:
方程f(x)=0有实数根
函数y=f(x) 的图象与x轴有交点
函数y=f(x)有零点
零点存在定理:
如果函数y=f(x)的图象在区间[a,b]上连续不断、且f(a)·f(b)<0,那么函数y=f(x)在区间[a,b]上必有零点.
问题1:你能求下列方程的解吗?
新知探究
问题2:以方程 为例,能不能确定方程根的大概范围呢?
回顾旧知:
问题2:以方程 为例,能不能确定方程根的大概范围呢?
新知探究
2
3
2.5
2.75
问题3:你有进一步缩小函数零点的范围的方法吗?
2.625
新知探究
二分法的定义:
概念形成
二分法的理论依据是什么?
想一想?
次数 区间长度:
1
2
3
4
0.5
所以方程的近似解为:
2.5
-0.084
2.5
3
0.25
0.125
0.0625
2.75
0.512
2.625
0.215
0.066
2.5625
2.5
2.75
2
3
由于|2.5625-2.5|=0.0625<0.1
2.5
2.75
2.65
2.5625
问题4:
初始区间(2,3)
且
探究归纳
1.确定区间[a,b],验证f(a)·f(b)<0,给定精确度ε;
3.计算f(c);
2.求区间(a,b)的中点c;
(1)若f(c)=0,则c就是函数的零点;
(2)若f(a)· f(c)<0,则令b= c(此时零点x0∈(a, c) );
(3)若f(c)· f(b)<0,则令a= c(此时零点x0∈( c, b) ).
4.判断是否达到精确度ε:即若|a-b|<ε,则得到零点近似值a(或b);否则重复步骤2~4.
例1:
x
y
0
x
y
0
0
x
y
0
x
y
A
D
c
B
概念拓展 实践探究
实践探究
想一想
如何确定初始区间
解:
记函数
x
y
0
2
x
y
0
2
x
y
0
2
概念拓展 实践探究
解:设 =x,则建立函数f(x)=x3-3,求f(x)的零点的近似值。
例3.不用计算器,求 的近似值(精确度0.01)
取a=1,b=2,f(1)=-2<0,f(2)=5>0,
x1=1.5,f(x1)=0.375>0,区间[1,1.5],
x2=1.25,f(x2)=-0.0469<0,区间[1.25,1.5],
x3=1.375,f(x3)=0.5996>0,区间[1.25,1.375],
概念拓展 实践探究
x5=1.28125,f(x5)=0.1033>0,区间[1.25,1.28125],
x6=1.26562,f(x6)=0.0273,区间[1.25,1.26562],
x7=1.25781,f(x7)=-0.1,区间[1.25781,1.26562],
∴ 1.26.
x4=1.3125,f(x4)=0.2610,区间[1.25,1.3125]
周而复始怎么办
定区间,找中点,
零点落在异号间,
口 诀
反思小结 体会收获
中值计算两边看;
区间长度缩一半;
精确度上来判断.
巩固提高 课外练习
1、课堂作业:
P92习题3.1A组 3、 4、 5
2、课外作业:
(1)阅读课本P91 《中外历史上的方程求解》;
(2)12只金表中有一只份量略轻,如何用一架天平秤,在秤量次数最少的情况下分辩出来?
