人教版九年级数学上册《投影与视图全章热门考点整合应用》授课课件(共34张ppt)
文档属性
| 名称 | 人教版九年级数学上册《投影与视图全章热门考点整合应用》授课课件(共34张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-04 21:12:49 | ||
图片预览









文档简介
(共34张PPT)
全章热门考点整合应用
第5章
投影与视图
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
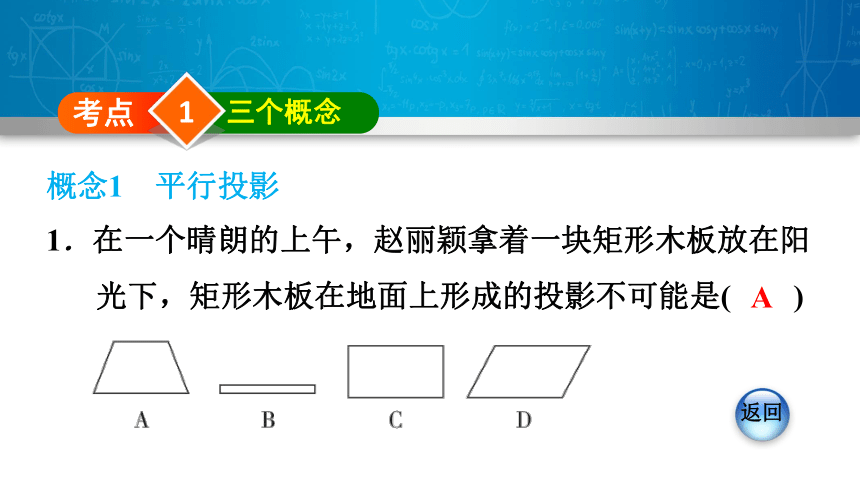
1.在一个晴朗的上午,赵丽颖拿着一块矩形木板放在阳光下,矩形木板在地面上形成的投影不可能是( )
返回
1
考点
三个概念
概念1 平行投影
A
2.如图,王斌同学想测量旗杆的高度,他在某一时刻测得1
m长的竹竿竖直放置时影长2
m.在同一时刻测量旗杆的影长时,因旗杆靠近教学楼,所以影子没有全落在地面
上,而是有一部分落在墙上,他测得落在地面上的影长为20
m,落在墙上的影高为2
m,求旗杆的高度.
返回
3.如图,一建筑物高为BC,光源位于点O处,用一把刻度尺EF(长22
cm)在光源前适当地移动,使其影子长刚好等于BC,这时量得O和刻度尺之间的距离MN为10
cm,
概念2 中心投影
O距建筑物的距离MB为20
m,问:该建筑物有多高?(刻度尺与建筑物平行)
返回
4.如图是一个由多个相同的小正方体搭成的几何体的俯视图,图中所标数字为该位置上小正方体的个数,则这个几何体的左视图是( )
概念3 三种视图
D
返回
5.如图是由一些棱长都为1
cm的小正方体组合成的简单几何体.
(1)该几何体的表面积为______
;
26
cm2
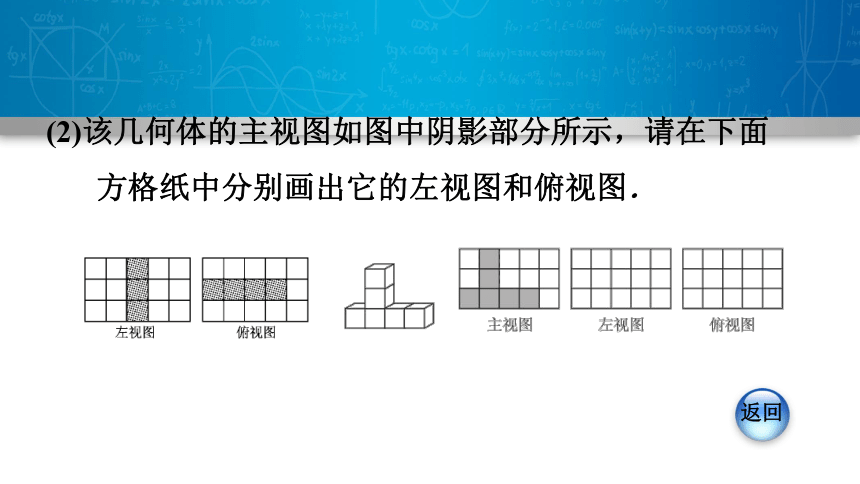
(2)该几何体的主视图如图中阴影部分所示,请在下面方格纸中分别画出它的左视图和俯视图.
返回
6.如图是一个由多个相同小正方体堆积而成的几何体的俯视图,图中所标数字为该位置上小正方体的个数,则这个几何体的左视图是( )
解法1 由三种视图还原几何体
2
考点
两个解法
返回
A
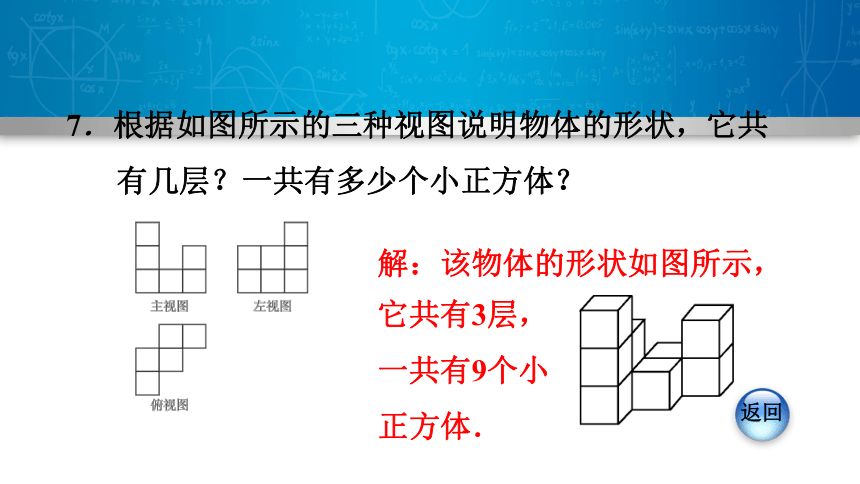
7.根据如图所示的三种视图说明物体的形状,它共有几层?一共有多少个小正方体?
解:该物体的形状如图所示,
它共有3层,一共有9个小正方体.
返回
8.如图是一个几何体的三种视图,它的俯视图为菱形.请写出该几何体的名称,并根据图中所给的数据求出它的侧面积.
解:该几何体是直四棱柱.由三种视图知,棱柱底面菱形的对角线的长分别为4
cm,3
cm.
∴菱形的边长为
cm.
∴棱柱的侧面积为
×8×4=80(cm2).
返回
9.某种含盖的玻璃容器(透明)的外形如图所示,请你画出它的三种视图.
解法2 分解图形法
10.在一次数学活动课上,李老师带领学生去测教学楼的高度.
3
考点
三个画法
画法1 画投影
如图,在阳光下,测得身高1.65
m的黄丽同学BC的影长BA为1.1
m,与此同时,测得教学楼DE的影长DF为12.1
m.
(1)请你在图中画出此时教学楼DE在阳光下的投影DF;
返回
(2)请你根据已测得的数据,求出教学楼DE的高度(结果精确到0.1
m).
11.小明和小丽在操场上玩耍,小丽突然高兴地对小明说:“我踩到你的‘脑袋’了.”如图为小明和小丽的位置.
(1)请画出此时小丽在阳光下的影子;
如图,AB即为所求.
(2)若小明的身高是1.60
m,小明与小丽间的距离为2
m,而小丽的影子长为1.75
m,求小丽的身高.
返回
12.学习投影后,小明和小颖利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图,在同一时刻,身高为1.6
m的小明(AB)的影子BC长是3
m,而小颖(EH)刚好在路灯灯泡的正下方H点,并测得HB=6
m.
画法2 画投影源
(1)请在图中画出形成影子的光线,并确定路灯灯泡所在的位置G.
(2)求路灯灯泡的垂直高度GH.
返回
13.一种机器上有一个转动的零件叫燕尾槽(如图),为了准确做出这个零件,请画出它的三种视图.
画法3 画三种视图
返回
14.如图,晚上,小亮走到大街上,他发现:当他站
4
考点
两个应用
应用1 测高的应用
在大街两边的两盏路灯(AB和CD)之间,并且自己被两边路灯照在地上的两个影子成一直线时,
自己右边的影子(HE)长为3
m,左边的影子(HF)长为1.5
m,又知自己身高(GH)为1.80
m,两盏路灯的高相同,两盏路灯之间的距离(BD)为12
m,求路灯的高.
返回
15.某天,小明和小亮来到一河边,想用遮阳帽和皮尺测量这条河的大致宽度,两人在确保无安全隐患的情况下,先在河岸边选择一点B(点B与河对岸岸边上一棵树的底部点D所确定的直线垂直于河岸).
应用2 测距离的应用
(1)小明在B点面向树的方向站好,调整帽檐,使视线通过帽檐正好落在树的底部点D处,如图所示,这时小亮测得小明眼睛距地面的距离AB=1.7
m.
(2)小明站在原地转动180°后蹲下,并保持原来的观察姿态(除身体重心下移外,其他姿态均不变),这时视线通过帽檐落在了DB延长线上的点E处,此时小亮测得BE=9.6
m,小明的眼睛距地面的距离CB=1.2
m.
根据以上测量过程及测量数据,请你求出河宽BD.
返回
全章热门考点整合应用
第5章
投影与视图
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
1.在一个晴朗的上午,赵丽颖拿着一块矩形木板放在阳光下,矩形木板在地面上形成的投影不可能是( )
返回
1
考点
三个概念
概念1 平行投影
A
2.如图,王斌同学想测量旗杆的高度,他在某一时刻测得1
m长的竹竿竖直放置时影长2
m.在同一时刻测量旗杆的影长时,因旗杆靠近教学楼,所以影子没有全落在地面
上,而是有一部分落在墙上,他测得落在地面上的影长为20
m,落在墙上的影高为2
m,求旗杆的高度.
返回
3.如图,一建筑物高为BC,光源位于点O处,用一把刻度尺EF(长22
cm)在光源前适当地移动,使其影子长刚好等于BC,这时量得O和刻度尺之间的距离MN为10
cm,
概念2 中心投影
O距建筑物的距离MB为20
m,问:该建筑物有多高?(刻度尺与建筑物平行)
返回
4.如图是一个由多个相同的小正方体搭成的几何体的俯视图,图中所标数字为该位置上小正方体的个数,则这个几何体的左视图是( )
概念3 三种视图
D
返回
5.如图是由一些棱长都为1
cm的小正方体组合成的简单几何体.
(1)该几何体的表面积为______
;
26
cm2
(2)该几何体的主视图如图中阴影部分所示,请在下面方格纸中分别画出它的左视图和俯视图.
返回
6.如图是一个由多个相同小正方体堆积而成的几何体的俯视图,图中所标数字为该位置上小正方体的个数,则这个几何体的左视图是( )
解法1 由三种视图还原几何体
2
考点
两个解法
返回
A
7.根据如图所示的三种视图说明物体的形状,它共有几层?一共有多少个小正方体?
解:该物体的形状如图所示,
它共有3层,一共有9个小正方体.
返回
8.如图是一个几何体的三种视图,它的俯视图为菱形.请写出该几何体的名称,并根据图中所给的数据求出它的侧面积.
解:该几何体是直四棱柱.由三种视图知,棱柱底面菱形的对角线的长分别为4
cm,3
cm.
∴菱形的边长为
cm.
∴棱柱的侧面积为
×8×4=80(cm2).
返回
9.某种含盖的玻璃容器(透明)的外形如图所示,请你画出它的三种视图.
解法2 分解图形法
10.在一次数学活动课上,李老师带领学生去测教学楼的高度.
3
考点
三个画法
画法1 画投影
如图,在阳光下,测得身高1.65
m的黄丽同学BC的影长BA为1.1
m,与此同时,测得教学楼DE的影长DF为12.1
m.
(1)请你在图中画出此时教学楼DE在阳光下的投影DF;
返回
(2)请你根据已测得的数据,求出教学楼DE的高度(结果精确到0.1
m).
11.小明和小丽在操场上玩耍,小丽突然高兴地对小明说:“我踩到你的‘脑袋’了.”如图为小明和小丽的位置.
(1)请画出此时小丽在阳光下的影子;
如图,AB即为所求.
(2)若小明的身高是1.60
m,小明与小丽间的距离为2
m,而小丽的影子长为1.75
m,求小丽的身高.
返回
12.学习投影后,小明和小颖利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图,在同一时刻,身高为1.6
m的小明(AB)的影子BC长是3
m,而小颖(EH)刚好在路灯灯泡的正下方H点,并测得HB=6
m.
画法2 画投影源
(1)请在图中画出形成影子的光线,并确定路灯灯泡所在的位置G.
(2)求路灯灯泡的垂直高度GH.
返回
13.一种机器上有一个转动的零件叫燕尾槽(如图),为了准确做出这个零件,请画出它的三种视图.
画法3 画三种视图
返回
14.如图,晚上,小亮走到大街上,他发现:当他站
4
考点
两个应用
应用1 测高的应用
在大街两边的两盏路灯(AB和CD)之间,并且自己被两边路灯照在地上的两个影子成一直线时,
自己右边的影子(HE)长为3
m,左边的影子(HF)长为1.5
m,又知自己身高(GH)为1.80
m,两盏路灯的高相同,两盏路灯之间的距离(BD)为12
m,求路灯的高.
返回
15.某天,小明和小亮来到一河边,想用遮阳帽和皮尺测量这条河的大致宽度,两人在确保无安全隐患的情况下,先在河岸边选择一点B(点B与河对岸岸边上一棵树的底部点D所确定的直线垂直于河岸).
应用2 测距离的应用
(1)小明在B点面向树的方向站好,调整帽檐,使视线通过帽檐正好落在树的底部点D处,如图所示,这时小亮测得小明眼睛距地面的距离AB=1.7
m.
(2)小明站在原地转动180°后蹲下,并保持原来的观察姿态(除身体重心下移外,其他姿态均不变),这时视线通过帽檐落在了DB延长线上的点E处,此时小亮测得BE=9.6
m,小明的眼睛距地面的距离CB=1.2
m.
根据以上测量过程及测量数据,请你求出河宽BD.
返回
